1. 引论
在代数拓扑和同调代数之间, 存在着一些奇妙的类比.
( 是交换环; 表示映射同伦类的集合; 表示在第 位置为 , 其余为 的上链复形)
在这份讲义中, 我们引入同伦代数的语言, 以解释这种类比. 当然, 同伦代数的功能远不限于此, 它已经在当代数学的很多分支中展现了威力. 1
什么是无穷范畴?
当代的同伦代数主要通过无穷范畴的语言来表述. 无穷范畴描述的是范畴的 “高阶结构”, 这在普通范畴论中是看不见的. 粗略地说, 一个无穷范畴由下列信息组成: 有一些对象, 有这些对象之间的态射, 而这些态射之间还有高阶的态射: 在普通态射之间有 -态射, 可以视为普通态射之间的同伦; 在 -态射之间还有 -态射, 可以视为 -态射之间的同伦, 如此等等.
我们将在几节之后再来严格地定义无穷范畴, 因为我们还要准备一些前置知识. 但现在, 我们可以看几个简单的例子, 以建立我们对无穷范畴的第一印象.
例 1.1. 考虑拓扑空间范畴 . 我们可以如下赋予其无穷范畴结构:
• | 对象: 拓扑空间. |
• | -态射 (对象之间): 拓扑空间之间的连续映射. |
• | -态射 (-态射之间): 连续映射之间的同伦. |
• | -态射 (-态射之间): 同伦之间的同伦. |
• | …… |
例 1.2. 对交换环 , 考虑 上的上链复形的范畴 . 我们可以如下赋予其无穷范畴结构:
• | 对象: 上的上链复形. |
• | -态射: 上链复形之间的链映射. |
• | -态射: 链映射之间的链同伦. |
• | -态射: 链同伦之间的链同伦. |
• | …… |
例 1.3. 对拓扑空间 , 考虑 的基本群胚 . 我们可以如下赋予其无穷范畴结构:
• | 对象: 中的点. |
• | -态射: 两个点之间的道路. |
• | -态射: 道路之间的同伦 (固定端点). |
• | -态射: 同伦之间的同伦. |
• | …… |
注意, 此时态射复合的结合律 并不严格成立, 而只是 “相差一个同伦” 成立 (因为相差一个参数化). 这也是无穷范畴理论中的一个主要的困难.
同伦范畴
在很多情况下, 无穷范畴都作为 (带额外结构的) 普通范畴的同伦范畴而得到. 下面, 我们来展示一个具体的例子.
定义 1.4. 范畴 定义如下:
• | 对象: 拓扑空间. |
• | 态射: 连续映射的同伦类. |
这里关键的想法是, 是在 中 “将所有同伦等价变得可逆” 而得到的范畴. 我们下面严格地描述这一过程.
定义 1.5. 弱等价范畴 (category with weak equivalences) 是二元组 , 其中 是范畴, 是一类态射, 满足如下性质:
• | 中所有同构都在 中. |
• | 满足三选二: 对 中任意图表如果 中有两个在 中, 那么第三个也在 中. |
例如, 二元组 是弱等价范畴, 其中 是 中所有同伦等价构成的类.
定义 1.6. 设 是弱等价范畴. 关于 的局部化 (localization) 是范畴 , 带有一个函子 , 满足以下泛性质:
• | 对任意函子 , 如果 将 中的所有态射都映到同构, 那么存在 (相差自然同构的意义下) 唯一的函子 , 使得图表在相差自然同构的意义下交换. |
大致来说, 范畴 就是在 中将所有 中的态射变得可逆而得到的范畴. 事实上, 通过这一想法, 可以给出 的一个具体构造.
构造 1.7. 设 是弱等价范畴. 定义范畴 如下: 其对象与 的对象相同, 其态射集 的元素为 中的态射列其中箭头可以向左或向右, 但向左的箭头必须在 中, 并且要商掉以下等价关系: 恒同态射可以直接去掉; 相邻同向箭头可以复合; 相邻异向箭头如果代表同一个态射, 就可以同时去掉.
不难验证 2上述构造确实满足定义 1.6 中的泛性质. 唯一的问题是态射集 可能太大, 而超出了集合允许的大小. 但我们暂时无视这个问题, 实在不行就换到一个更大的宇宙也无妨.
命题 1.8. .
事实上, 我们将看到, 局部化能给出高阶范畴结构. 在此例中, 普通范畴 仅仅是局部化给出的第一层信息, 而完整的信息需要通过一个无穷范畴来刻画. 在这里, 这个无穷范畴正是例 1.1 给出的无穷范畴 .
上述例子中的高阶范畴结构具有十分清晰的描述: 连续映射间的同伦, 同伦间的同伦, 等等. 我们可能希望在其它类似的情况下, 局部化得到的无穷范畴也能有这样的具体描述. 例如, 在同调代数中, 我们将拟同构变得可逆, 而得到导出范畴, 我们希望在对应的无穷范畴中, 高阶态射也能被具体地描述为同伦、同伦的同伦, 等等. 事实上, 这是可以做到的, 只需借助模型范畴 (model category) 这一工具.
模型范畴是带有一些额外结构的弱等价范畴. 模型范畴将帮助我们在无穷范畴中进行计算, 有人认为 3这就类似于局部坐标能帮助我们在流形上进行计算.
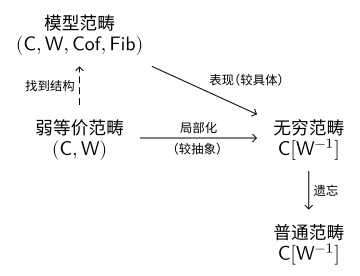
以上漫谈总结于下图.
第一次尝试
下面, 我们试着写下高阶范畴的一种简单但 “错误” 的定义. 我们知道, 高阶范畴也就是普通范畴加上高维的箭头, 这一结构似乎并不复杂, 我们来将它描述清楚.
定义 1.9. 幺半范畴是指范畴 , 带有以下结构:
• | 一个函子称为张量积. |
• | 一个对象 , 称为 的单位对象. |
• | 三个自然同构分别称为结合子、左单位子、右单位子. |
它们满足以下条件:
• | (三角形公理) 对任意 , 有交换图 |
• | (五边形公理) 对任意 , 有交换图 |
注 1.10. 对于 个以上的对象, 也可以谈论五边形公理的类似物, 也就是 Stasheff 结合多面体对应的图表. 在范畴代数中可以证明 4, 五边形公理保证了所有这些结合多面体图表都交换, 因此, 我们不需要更多公理.
以下给出幺半范畴 的一些例子:
• | , 其中 是单点集. |
• | , 其中 是不交并. |
• | , 其中 是终对象, 即空乘积. |
• | , 其中 是始对象, 即空余积. |
• | , 其中单位对象 在第 个位置, 上链复形的张量积定义为 |
定义 1.11. 设 是幺半范畴. 一个 -充实范畴 由以下信息组成:
• | 一类对象 . |
• | 对 , 有一个态射对象它是 的对象, 视作 之间所有态射构成的空间. |
• | 对每个对象 , 有一个恒同态射它是 中的态射, 可以视为对象 中的一个 “元素”. |
• | 对每三个对象 , 有一个复合态射它是 中的态射. |
它们满足以下条件:
• | 任何态射复合恒同态射都等于它自身. |
• | 复合满足结合律. |
这两个条件的严格叙述留给读者完成, 也可参见充实范畴一文.
例如, 普通范畴就是充实于 的范畴.
在某些情况下, 有遗忘函子 , 并且它保持幺半范畴的结构. 此时 -充实范畴就能看成是带额外结构的普通范畴, 以下几例均如此.
例 1.12. 范畴 充实于自身, 因为对 , 集合 可以赋予紧开拓扑, 使得复合映射是连续的.
例 1.13. 范畴 充实于自身. 对 , 定义上链复形 如下: 其中 不一定是链映射, 其微分定义为这样, 所有链映射就是这个链复形的所有 -上圈 (cocycle), 也对应于单位对象 到该上链复形的链映射, 也就是该上链复形的一个 “元素”.
例 1.14. 所有小范畴的范畴 充实于自身, 因为对 , 有函子范畴 , 其对象为 的函子, 态射为函子间的自然变换.
我们现在可以使用充实范畴的语言, 给出高阶范畴的第一个定义了.
定义 1.15. 严格 -范畴是充实于 的范畴.
例如, 就是一个严格 -范畴, 其中 -态射是范畴间的函子, -态射是函子间的自然变换.
任何 -充实范畴都能看作严格 -范畴, 因为我们可以将态射空间 (此时为拓扑空间) 替换为其基本群胚. 此时, -态射是态射空间中的点, -态射是态射空间中的路径 (的同伦类). 例如, 自身就是一个严格 -范畴, 其 -态射是映射间的同伦 (的同伦类).
然而要注意, 对拓扑空间 而言, 基本群胚 不是严格 -范畴, 因为正如上文所言, 其中 -态射的复合并不严格满足结合律. 这意味着我们的定义过于严格, 从而是 “错误” 的.
不过我们将错就错, 继续给出 -范畴和 -范畴的定义. 这些定义并不会在下文使用.
定义 1.16. 对 归纳, 定义严格 -范畴为充实于 -范畴的范畴.
定义 1.17. 严格 -范畴是一个序列其中 是严格 -范畴, 使得每个 是在 中扔掉所有 -态射得到的 -范畴.
-范畴
虽然我们尚未严格定义一般的 -范畴与 -范畴, 但我们其实已经大概知道它们是什么了. 因此, 我们可以来半严格地讨论它们的性质.
定义 1.18. 设 且 . -范畴指一个 -范畴, 其中所有 -态射都可逆.
注意, 这里提到的 范畴不一定是严格 -范畴, 因此 “可逆” 实际上指的是 “相差同伦的意义下可逆”, 也就是 “具有同伦逆”. 我们来看一些例子.
• | 普通的范畴也就是 -范畴. |
• | 普通的群胚也就是 -范畴. |
• | 以上定义的严格 -范畴都是 -范畴的特例, 而严格 -范畴是 -范畴的特例. |
• | 我们常称 -范畴为 -群胚. 这是一类十分重要的结构, 因为它是同伦型的一种自然定义. 有一种叫做同伦类型论 [HoTT] 的理论, 致力于以 -群胚取代传统的集合论, 而重新搭建数学的基础. |
• | 充实于 -范畴的范畴可以视为 -范畴. |
• | 是 -范畴, 因为映射的同伦都是可逆的: 同伦与其逆同伦的复合同伦于恒同同伦. |
• | 是 -范畴, 因为链同伦的复合定义为链复形间映射的加法, 而链同伦加上负的自己等于 , 这里 就是恒同同伦. |
• | 对拓扑空间 而言, 基本群胚 是 -群胚. 它描述了 的同伦型. |
在上述第五点的意义下, 对 , 我们也能定义 -范畴的概念. 我们将看到, 最合理的定义如下:
• | -范畴是集合. |
• | -范畴是偏序集. |
• | -范畴是 或单点集, 也可视为一个真假值. |
• | -范畴是单点集, 可以视为 “真”. |
高阶范畴学家相信, 范畴的底层应该是 , 并且该给所有范畴重新编号, 使得 变成 , 变成 , 等等. 这样, 在数学的摩天大厦里, 逻辑学住在一层, 集合论住在二层, 而范畴论住在三层. 由此观之, 将整个大厦视为整体似乎更加自然. 这大概也是高阶范畴论有希望取代集合论, 而建立数学基础的原因之一.
脚注
1. | ^ 例如, nLab 页面 applications of (higher) category theory 列举了这套理论的若干应用. |
2. | |
3. | ^ 见 MathOverflow 问题 Do we still need model categories? 中的回答. |
4. |