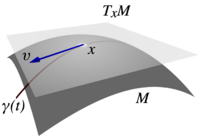
切空间
光滑流形 在某点 处的切空间, 记为 , 是由该点处所有 “与 相切的向量” 构成的实向量空间. 该向量空间的维数与 的维数相等, 其元素称为切向量. 例如, 曲线的切线、曲面的切平面都是切空间的特例.
应更换更简洁的插图.
将光滑流形 在所有点处的切空间粘起来, 可以得到 上的光滑向量丛 , 称为其切丛.
1定义
切空间可以对一般的光滑流形定义, 但该定义比较抽象. 另一方面, 对 Euclid 空间 的子流形 而言, 切空间具有更直观的定义. 我们先叙述这种直观的定义, 再叙述更抽象的一般定义.
对 Euclid 空间的子流形
由上述定义, 只能看出切空间为 的子集, 而不能直接得出其为子向量空间.
命题 1.2. 定义 1.1 中的切空间 确实是 的子向量空间, 其维数等于 的维数.
另一方面, 这一定义取决于流形在 Euclid 空间中的嵌入, 而不能直接看出切空间是流形内蕴的信息. 下面的一般定义解决了这一问题.
一般定义
定义 1.3 (切空间). 设 是光滑流形, 设 . 则
• | 在 处的切向量是指一个线性函数满足对任意 , 有 Leibniz 法则这里, 我们把 理解成函数 在点 处沿着向量 的方向导数. |
• | 在 处的切空间 是 在 处的所有切向量构成的向量空间. |
例 1.4. 若 为光滑映射, 即 上的光滑曲线, 我们可以将 以如下方式视为 的切向量 (定义 1.3): 对 , 定义这也就是 沿 的方向导数. 不难验证这一定义满足 Leibniz 法则, 从而确实给出了 的切向量. 这一例子实际上是切映射的特例.
对复流形
...
2性质
基本性质
我们首先验证一些初步的性质. 例如, 我们证明切空间的维数等于流形维数, 并验证每个切向量都可以通过光滑曲线以类似定义 1.1 的方式给出, 从而该定义确实等价于定义 1.3.
引理 2.1. 设 是光滑流形, , 设 是切向量 (定义 1.3). 则对 而言, 只取决于 在 附近的取值. 换言之, 如果 在 的一个邻域内相同, 那么 .
引理 2.2. 设 是 维光滑流形, . 则有向量空间同构 .
引理 2.3. 向量空间 的维数是 , 它的一组基是
推论 2.4. 设 是 维光滑流形, . 则切空间 (定义 1.3) 是 维实向量空间.
推论 2.5. 设 是光滑流形, 设 . 则对每个 (定义 1.3), 存在光滑曲线 , 使得 , 且 , 其中 是例 1.4 中定义的切向量.
特别地, 若 是子流形, 则 的切空间确实由定义 1.1 给出. 更特别地, 定义 1.1 定义的切空间确实是实向量空间.
3相关概念
术语翻译
切空间 • 英文 tangent space • 法文 espace tangent