7. 基本群 (I)
Poincaré 如是说. Ce n’est pas assez, en effet, qu’une science soit légitime : il faut que l’utilité ne puisse en être contestée. Tant d’objets divers sollicitent notre attention, que les plus importants ont seuls droit de l’obtenir.1
代数拓扑学始于 Henri Poincaré 的 1892 年的长文 “位置分析 (Analys Situs)”. 本节要介绍的基本群 (fundamental group), 或谓 Poincaré 群, 是 Analysis Situs 一文中引入的第二个与拓扑相关的代数结构 (第一个是流形的同调群). 在这一节中我们只介绍最简单的概念和计算. 主要的计算工具将在下一节介绍.
7.1映射的同伦
设 和 是两个从拓扑空间 到拓扑空间 的连续映射. 则一个从 到 的同伦 (homotopy) 是一个连续映射它满足, 对任意 , 有 , . 若存在从 到 的同伦, 我们就称 与 同伦 (homotopic), 有时记作 . 同伦于常值映射的连续映射叫做零伦的 (nulhomotopic).
命题 7.1.1. 令 为拓扑空间. 则集合 上的关系 “ 同伦于 ” 是个等价关系.
证明. 对映射 , 常值同伦 给出了 .
如果 是从连续映射 到连续映射 的同伦, 那么 “相反同伦” 是从 到 的同伦. 从而同伦是对称的关系.
关于同伦关系的商集合记为 . 映射 的同伦类记作 .
例 7.1.2. 设 为只有一个点的拓扑空间. 则 到拓扑空间 的连续映射一一对应于 上的点. 而 到 上两个映射的同伦则相当于连结 上两个点的道路. 通过一一对应 与 , 同伦关系变成了 上 “可以被道路连结” 这个关系. 因此我们得到了一一对应: , 其中 代表了拓扑空间 的道路连通分支构成的集合.
命题 7.1.3. 设 和 为拓扑空间. 设从 到 的连续映射 , 同伦, 以及 从 到 的连续映射 , 同伦. 则复合映射 与 同伦.
因此, 映射的复合尊重同伦关系, 因此诱导了自然的映射 (“映射同伦类的复合”)映射复合的结合律推出了同伦类的复合的结合律.
我们称同伦类 为同伦等价 (homotopy equivalence, Bourbaki 术语 homéotopie), 如果存在 , 使得 , . 此时称 与 互为同伦逆.
7.1.4 (与同伦等价有关的概念与例子).
1. | 如果拓扑空间 和 通过映射 同伦等价, 那么对任何拓扑空间 , 自然映射 都是一一映射. 特别地, 如果 是单点拓扑空间, 利用 例 7.1.2, 我们得知 的道路连通分支一一对应于 的道路连通分支. |
2. | 同伦等价于一个点的拓扑空间叫做可缩 (contractible) 的. 实数空间 中的星形子集都是可缩的. 事实上, 设 是星形的, 即存在点 , 使得对任意 , 线段 . 则我们断言常数映射 和包含映射 互为同伦逆. 事实上, , 只需证明 同伦于恒等映射. 这个同伦可以由 给出. |
3. | 令 为拓扑空间, 为 的子空间. 则一个从 到 的形变收缩 (deformation retraction) 是一个同伦 使得 , , 并且对任意 中的点 , 中的点 , 有 . 如果存在从 到子空间 的形变收缩, 那么我们就说 是 的一个形变收缩核 (deformation retract). 如果 是 的形变收缩核, 那么 与 同伦等价, 因为形变收缩 给出了包含映射 的同伦逆. 比如, 映射 就给出了 到 的形变收缩. Möbius 带 (例 2.4.2) 的中心圆周是 Möbius 带的形变收缩核. |
7.2变体
我们介绍上小节的一些概念的变体.
1. | 设 是 拓扑空间 的子空间. 我们称同伦 是固定 的, 如果对任意 , 是常值映射. 如果存在一个固定 的从 到 的同伦, 自然有 , 并且我们称 与 相对于 同伦 (homotopic relative to ), 记作 . |
2. | 一个带基点的拓扑空间 (pointed space) 是指一个偶对 , 其中 是拓扑空间 上一点. 带基点拓扑空间 , 之间的一个保持基点的连续映射是指一个满足 到从 到 的连续映射. 保持基点的连续映射构成了函数空间 的子空间 . |
3. | 两个保持基点的连续映射 之间的一个保持基点的同伦是指一个固定 的同伦, 即连续映射 满足, 对任意 , 有 . 照搬命题 7.1.1 的证明, 我们知道保持基点的同伦是集合 上的一个等价关系, 它的等价类记作 . 类似于命题 7.1.3, 带基点的映射的保持基点的同伦类之间也可以复合, |
4. | 可以定义带基点的拓扑空间之间 “保持基点同伦等价” 的概念. 这个概念比相对应的拓扑空间彼此同伦等价要强. 带基点的拓扑空间 保持基点地同伦等价于 , 当且仅当 是 的形变收缩核. 但习题 7.7.6 提供了一个带基点的空间 的例子, 拓扑空间 本身同伦等价于单点空间, 但它上面任何的点都不是形变收缩核. |
7.3道路的同伦与基本群
在本节中, 我们采用如下术语.
拓扑空间 上的一条道路是指一个连续映射 . | |
道路 叫做一个基于点 的回路, 如果 . 令 为标准的商映射, . 则一个基于 的回路等价于一个保持基点的连续映射 . | |
若 是从 到 的道路, 它的相反道路是 它是从 到 的道路; | |
基于 的常值道路 是指常数映射 . |
定义 7.3.1. 拓扑空间上两条道路 , 之间的一个道路同伦 (path homotopy) (或严格同伦 (strict homotopy)) 是一个同伦 它还满足 特别地, 和 有相同的出发点和终点. 如果 与 道路通伦, 我们用记号 表示.
如果用 表示一切从 出发, 终于 的 上的道路. 则道路同伦给出了 上一个等价关系.
定义 7.3.2. 令 , 为两个 拓扑空间 上的道路, 满足 . 定义它们的乘积道路为
命题 7.3.3. 令 为拓扑空间 上的道路. 则 道路同伦于基于 的常值道路.
命题 7.3.4. 令 与 为拓扑空间 满足 的道路. 假设有道路 , 满足 则 .
命题 7.3.5. 令 与 为拓扑空间 上的三条道路. 假设 , . 则有
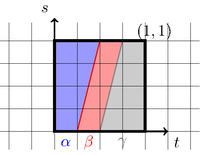
证明. 这个可以通过图 1 看出来.
图 1: 的结合律
定义 7.3.6. 对于拓扑空间 , 令 , 即 到 的道路的道路同伦类. 则上面的讨论说明, 对任何的 , 道路的乘积给出了良好定义的映射 并且这个映射满足 “结合律” .
若 , 则它相反道路的道路同伦类满足 因此, 我们用形象的记号 来表示道路同伦类 .
特别地, 回路之间的同伦类的乘积给出了集合 上一个满足结合律的二元关系, 这个二元关系给出了一个群运算: 常值道路是群的单位元, 而相反道路提供了逆元. 群 叫做带基点的空间 的基本群 (fundamental group), 或 Poincaré 群.
我们称一个道路连通拓扑空间为道路单连通 (simply connected by paths) 的, 如果对任何 , 有 是平凡群.
7.4基本群的初步性质
对基点的依赖
命题 7.4.1. 令 为道路连通拓扑空间. 则对任何 , 基本群 与 是同构的.
系 7.4.2. 设 是拓扑空间. 则下面的陈述等价.
是平凡群. | |
任何两条始于 且具有相同终点的道路都严格地同伦. | |
任何基于 的回路都严格同伦于基于 的常值道路. |
例 7.4.3. 考虑空间 . 对任何基于原点的回路 , 定义 , . 则 就是一个从回路 到基于原点的常值道路的严格同伦. 因此对一切 , 我们有 .
注 7.4.4.
1. | 如果 是两个道路同伦类, 且 有意义 ( 和 由首尾相连的道路代表), 那么 . |
2. | 如果取不同的两个元素 , 则同构 与 未必相同. 因此, 虽然不同基点的基本群是同构的, 但却不是 “典则同构” 的. |
函子性质
设 为拓扑空间之间的连续映射. 对 上连结两点 的道路 , 复合映射 是 上连结 与 的道路. 根据命题 7.1.3 (的关于严格同伦的变体), 诱导了集合之间的映射由于映射 尊重严格同伦类的毗连, 即特别地, 如果 , 我们就得到了基本群之间的同态在不至于引起误会的前提下, 这个同态通常被简写为 . 如果 , 是两个连续映射, 那么 作为从 到 的同态, 成立特别地, 如果 是同胚, 那么 是群的同构.
然而基本群不仅仅是同胚的不变量, 它还是同伦的不变量. 更准确的说法是下面的命题.
命题 7.4.5. 令 与 是两个拓扑空间, , 是两个由 到 的连续映射, 并且可以通过同伦 相连. 令 , , , 以及 . 则
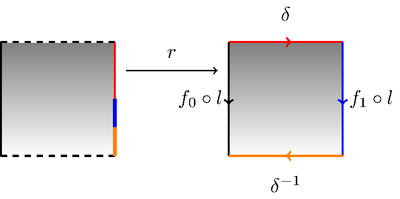
证明. 令 为 中的一个严格同伦类, 由道路 代表. 则复合映射 给出了回路 与回路 的同伦. 今构造正方形 与商空间 的如图 2 所示的同胚: 虚线部分要被坍缩掉, 而左侧具有某种颜色的部分要被同胚地映射到具有相同颜色的地方 (具体同胚留给读者构造).
图 2: 同伦与固定基点的同伦
系 7.4.7. 若连续映射 是从拓扑空间 到拓扑空间 的一个同伦等价, 那么 是同构.
自由同伦的回路
定义 7.4.9. 我们称拓扑空间 上的两个回路 , 是自由同伦 (freely homotopic) 的, 如果存在同伦 满足 , , . 即, 对任何 , 道路 是回路.
通过商映射 , 我们可以将任何回路看作从 到 的连续映射. 若用 代表 在 中的像, 那么基于 的两个回路固定基点地同伦相当于它们在集合 中是同一个元素; 而它们自由同伦则是在说它们在集合 中是同一个元素. 在这一小段中, 我们来澄清固定基点同伦类和自由同伦类的关系.
命题 7.4.10. 令 为道路连通的拓扑空间, 是 上的点. 则 上任何的回路都自由地同伦于一个基于 的回路.
命题 7.4.11. 设 为拓扑空间, 是 上的点. 令 和 为两个基于 x 的回路. 则 与 自由同伦的必要且充分条件是存在 , 使得 .
积空间的基本群
命题 7.4.13. 设 是一族带基点的拓扑空间. , 以 为基点. 则 同构于乘积群 .
7.5球面的基本群
命题 7.5.1.
1. | 去掉原点的平面 上任意两条自由同伦的回路有相等的环绕数. |
2. | 回路的环绕数给出了群同构 . |
证明. 首先我们需要说明环绕数在道路的自由同伦类上是常值. 事实上, 我们来证明定义 6.4.1 中的 “接近” 与自由同伦是同一个概念. 按照那里的论证, 由于非常接近的回路可以通过线段互相形变, 接近的回路是自由同伦的. 设 为从回路 到回路 的自由同伦. 由于 连续, 的所有凸开集关于 的逆像构成了 的覆盖. 根据 Lebesgue 数引理, 命题 6.2.4, 存在方形的分割 使得每个小方形 在 下的像都落入某个 的凸开集中. 特别地, 回路 与 在定义 6.4.1 的意义下非常接近. 从而 与 接近. 这就证明了第一个断言.
第二个断言的证明. 对任何两条基点为 的可微回路 , , 微积分换元公式告诉我们 . 由于命题 6.4.2 告诉我们任何固定基点的同伦类都可以由可微映射代表, 上面的公式就说明环绕数给出了群同态.
这是一个满同态, 因为 的环绕数是 .
由于 是 的一个形变收缩核 (见 7.1.4/3), 系 7.4.7 推出如下结论.
为了计算 的基本群, 我们先证明下述结论, 它是接下来要证明的 Seifert–van Kampen 定理的特殊情形.
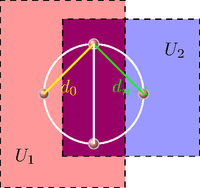
命题 7.5.3. 设 , 为拓扑空间 的两个道路连通, 道路单连通开集. 若 , 且 道路连通, 那么 是道路连通且道路单连通的拓扑空间.
注意: 在使用这个命题时, 不能将 “开集” 换做 “闭集”. 一个反例由所谓的 “Griffiths 孪锥” 提供.
若 , 则 中的单位球面 可以由两个同胚于 的开集覆盖, 并且 道路连通. 根据命题 7.5.3, 我们得到如下结论.
根据命题 7.4.13, 环面 的基本群同构于加法群 . 因此, 环面与球面不同胚.
命题 7.5.3 的证明. 令 . 则利用 的道路连通性可知任意 都可以与 通过道路相连. 于是 是道路连通的.
令 为一条基于 的回路. 利用 Lebesgue 数引理 (命题 6.2.4), 存在 的分划 使得 要么完全落在 中, 要么完全落在 中. 令 . 令 为一条从 出发到 中止的道路. 如果 , 我们要求 也完全落入 中. 令 , 则 并且对任何的 , 回路 的像要么完全落入 , 要么完全落入 . 由于 是道路单连通的, 它必须严格同伦于基于 的常值道路. 同理, 严格同伦于 .
图 3: 逐次取消回路
Jordan 分离定理
定理 7.5.5. 令 为 中同胚于 的子空间. 则 不连通.
我们将展示的证明属于 P. H. Doyle. 下面所处理的空间都是局部道路连通的, 所以探讨连通性和道路连通性没有差别, 我们不再嘱咐读者了.
第一步, 我们将 看作 去掉一点而得到的子空间 (比如利用球极投影). 下面的命题说明, 只需证明 是不连通的.
命题 7.5.6. 和 的连通分支数一样多.
证明留作习题.
第二步, 选择 . 利用 处球极投影, 我们可以将 同胚地映射成 的同胚于 的闭子空间 , 于是 同胚于 . 因此, 只需证明 挖掉一个同胚于 的闭子空间之后不连通. 为此, 我们用反证法, 假设 连通.
证明的要点是将 看作 的由 定义的子空间, 并且考察 的基本群. 我们利用两种方法来计算 .
方法一: 利用命题 7.5.3 直接计算. 令以及则 . 利用直线同伦, 可以看出 分别是 的形变收缩核. 因此, 可缩. 类似地, 以 为形变收缩核. 因此, 若 连通, 那么 道路单连通.
方法二: 利用 的自同胚将 化成 “好” 的形式后直接计算. 事实上, 我们来构造一个 的自同胚 , 使得 是 -轴 . 如果这件事情完成了, 就有 , 而 同伦等价于 , 故而基本群是 . 这就与方法一中的计算矛盾. 从而 Jordan 的定理得证.
因此证明的最后一步就是找到上面的同胚. 固定同胚 , 记它的逆映射为 . 利用 Tietze 扩张定理, 可以把 扩张成连续映射 . 定义则 显然是同胚. 与每个平面 都只交一个点 . 利用这个观察, 定义同胚则 即为所求.
事实上, 恰好有两个连通分支 (“Jordan 曲线定理”). 上述论证完全可以推出这个定理, 但需要借助命题 7.5.3 的升级版本: 假如 , 是局部道路连通拓扑空间 的道路单连通开集, , 则 同构于 由 去掉一个元素后生成的自由群. 我们会在讲解一般 van Kampen 定理时处理上面的断言.
7.6箭图与广群
这一节我们介绍一些代数结构.
定义 7.6.1. 一个箭图 (quiver) 是一个四元集合 , 其中 是一个集合, 其中的元素叫做箭图的 “顶点”, 是一个集合, 其中的元素叫做箭图的 “箭头”, 是两个从 到 的映射. 对于箭头 , 叫做 的起点, 叫做箭头的终点. 下图描绘了一个有两个顶点, 四个箭头的箭图: 对于箭图 , 有时用 , , , 来分别代表 . 对任意两个顶点 , 我们用记号 来代表集合
定义 7.6.2. 令 为一个箭图. 令 为 的子集, 它包含了一切偶对 , 满足 . 上的合成法则 (composition law) 是指一个从 到 的映射 , 它对任何满足 的箭头 , 指定了一个箭头 .
我们称合成法则满足结合律, 如果对任意 , , 成立
我们称箭头 是合成法则 的幺元, 如果对任何 , 任何 , 任何 , 有 , .
定义 7.6.3. 一个范畴 (category) 是一个偶对 , 其中 是一个箭图, 是 上满足结合律的合成法则, 并且对任何 , 中有幺元. 在一个范畴中, 我们通常将 记做 或者毗联 (或者 , 注意顺序是相反的).
一个从范畴 到范畴 的函子 (functor) 是一个偶对 , 其中 是从 到 的映射, 是从 到 的映射, 满足
, | |
, | |
如果 , , 那么在 中成立等式 |
一个广群 (groupoid, 或译为 “群胚”) 是一个范畴 , 它满足如下性质: 对任意 , 存在 , 满足 , . 如果 是一个广群, 那么对 的顶点 , 集合 是一个群.
例 7.6.4 (基本广群). 令 是拓扑空间. 令 . 定义 为满足 的映射. 类似地, 定义 定义 为满足 的映射. 则 构成了一个箭图. 道路的同伦类的复合给出了一个 上的合成法则. 在这个合成法则下, 构成了一个广群, 叫做 的基本广群 (fundamental groupoid), 或 Poincaré 广群.
例 7.6.5 (置换广群). 令 是集合之间的映射. 对 , 令 ; 对 , 令 为一切从 到 的双射. 令 , , , , 则 是一个广群. 对于 , , 它们的合成法则由映射的复合给出: 广群 叫做 相对于 的置换广群 (permutation groupoid), 通常记作 .
一个广群 在 上相对于 的右作用是一个广群态射 于是对于可复合的 , 成立 .
7.7习题
7.7.1. 证明, 如果拓扑空间 与 拓扑空间 同伦等价, 与 拓扑空间 同伦等价, 那么 与 同伦等价.
7.7.2. 证明 Hilbert 空间 (习题 2.6.9) 的子空间 是可缩的.
7.7.3. 令 为拓扑空间. 我们称 的 Lyusternik–Schnirelmann 畴数 为 , 如果存在 的开覆盖 , 其中每个包含映射 都零伦, 并且 是最小的能够保证这样开覆盖存在的整数.
1. | 拓扑空间 的纬悬 (suspension) 是商空间 . 证明 , 且 当且仅当 可缩. |
2. | 令 为 , 其中 是 上三个不同点. 求 . |
3. | 证明 . [利用一点上同调的性质可以证明, 的 Lyusternik–Schnirelmann 畴数等于 .] |
4. | 如果 与 同伦等价, 则 . |
7.7.4. 一般线性群 同伦等价于实正交群 ; 一般线性群 同伦等价于酉群 .
7.7.5. 令 为梳子空间 (例 5.6). 令 为以 为对称中心的中心对称. 证明 可缩, 但是 不可缩.
7.7.6. 下面的 (2), (3) 两款是 Bourbaki, TA III, p. 321, Exercise 1.
1. | 设 是拓扑空间 的单点子空间. 如果 是 的形变收缩核, 那么存在 的开邻域 , 使得包含映射 是零伦的. |
2. | 令 为 中连结 和 的线段. 证明 是 的形变收缩核, 但 上任何其它点都不是 的形变收缩核. |
3. | 证明 是可缩的, 但任何 的点都不是 的形变收缩核. |
7.7.7. 令 为恒等映射到自己的一个同伦. 则对于任何 上的点 , 证明道路 落在 的中心里.
7.7.8 (一些空间的基本群的计算). 计算下列空间的基本群.
1. | |
2. | . |
3. | 设 是简约的梳子空间 (例 5.6), 令 赋予 的子空间拓扑. 求 . |
4. | 复射影空间 . |
7.7.9. 令 为子空间的包含映射. 如果 是 的收缩核 (习题 3.8.2), 证明对任意 , 映射 是单射. 利用这个性质说明 Möbius 带的边界圆周不是 Möbius 带的收缩核.
7.7.10. 证明命题 7.5.6.
7.7.11. 对正整数 , 阶正交矩阵可以看作球面 到自己的连续映射. 什么时候两个 阶正交矩阵给出同伦的映射?
7.7.12. 这个习题致力于证明 Poincaré 的髮球定理: 任何 上的连续切向量场必然有零点.
1. | 球面 上的一个连续切向量场是连续映射 , 满足 (向量的内积) 对任何 都为零. 验证 是 上的切向量场. 找出它的零点. 在草稿纸上画一下这个向量场的模样. |
2. | 令 , , , 分别为从 和 出发的球极投影 (用平面 来承接投影, 下标中的 , 只是为了区别到达域). 定义 , 利用多变量微分学里学到的概念, 解释为何 上的连续切向量场等价于两个连续 (列) 向量值函数 , , 满足 (如果没学过多变量微分学有关内容, 读者也可以用这一款的描述来定义切向量场.) |
3. | 令 为球面 的赤道 (球面上坐标 的点). 证明, 如果连续切向量场 没有零点, 那么 与 看作映射 都是零伦的. |
4. | 验证向量值函数 在 上的限制具有环绕数 , 从而推出 Poincaré 的定理. |
脚注
1. | It is not enough, in fact, for a science to be legitimate; its utility must be incontestable. So many objects demand our attention that only the most important have the right to be considered. |