3. 粘贴
在这一节中, 我们要介绍拓扑学中构造空间的一个基本手段: 粘贴. 比如, 圆周 应该可以通过将闭区间 的两个端点 , 粘接在一起而得到; Möbius 带应该可以通过将方形 的一对对边沿相反方向粘接而得到. 在拓扑中描述 “粘贴” 这个概念可以通过 “商映射” 和 “商拓扑” 来实现.
3.1关系与等价关系
我们的目的是要 “粘合” 拓扑空间. 作为准备工作, 我们先来描述如何在集合的层面上实行 “粘合”. 它在数学上对应的概念叫做 “等价关系的等价类”.
定义 3.1.1. 令 为一个集合.
1. | 上的一个关系 (relation), 或对应 (correspondence) 是乘积集合 的一个子集 . 如果 , 我们用符号 “” 表示, 并且称元 素 与 (关于关系 ) 相关. 上的关系通常用下图 来表示. 横着的两个箭头是两个投影映射在 上的限制. 更一般地, 任何两个映射 可以给出一个映射 . 从而给出一个关系 . |
2. | 关系 叫做自反 (reflexive) 的, 如果 对任何 都成立. 关系 叫做对称 (symmetric) 的, 如果 对任何 , 推出 . 关系 叫做传递 (transitive) 的, 如果对任何 , 和 推出 . 关系 叫做一个 等价关系 (equivalence relation), 如果它是对称的, 自反的, 传递的. |
3. | 显然, 自己就是一个等价关系. 这个等价关系下, 任何两个元素都 “相关”. 任何关系 都决定了一个等价关系 , 这里 是 一切包含 的等价关系的交 (这个交是非空的, 因为 ). 等价关系 叫做由 生成的等价关系 (equivalence relation generated by ). |
4. | 设 是集合 上的一个等价关系. 则对任何 , 元素 关于 的等价类 (equivalence class) 是集合 即 的等价类包括了一切 “与 有关” 的 中元素. 集合 中任何元素都叫做等价类 的代表元 (representative). 对同一等价类的 两个代表元 , 我们有 . |
5. | 集合 关于等价关系 的一切等价类的全体构成一个集合, 称为 关于 的商集 (quotient set), 记作 . |
我们提供几个简单的例子.
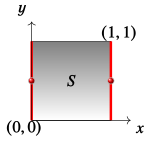
例 3.1.2. 假设我们要将下图所示的方形区域 的两条竖边纵坐标相等的点粘合起来, 作为集合我们所需要实行的操作如 下. 我们在矩形纸条这个集合上引入等价关系 , 我们宣布
, , | |
, |
图 1: 粘合正方形两条边
则 关于 的商集, 作为集合, 就与圆柱的边界曲面一一对应了.
例 3.1.3. 在算术中常见的等价关系是同余. 令 为整数, 我们说整数 与 模 同余 (congruent modulo ), 记做 , 如果 能够被 整除. 容易验证 是 上的等价关系. 它的等价类被记 作 .
例 3.1.4. 令 为一个映射. 我们宣布 当且仅当 . 容易验证 是等价关系. 它的等价类恰好是映射 的纤维. 事实上, 任何等价关系都可以实现为某个映射 . 如果 是 上等价关系, 则将元素 映射到它的等价类 定 义了一个满映射 . 这个映射在等价类 上的纤维就是这个等价类里 的元素. 于是 .
映射 满足如下泛性质: 如果 是任何映射, 满 足(即在 的纤维上, 是常值, 或 等价地, , 其中 是投影映射在 上的限制), 则存在唯一的映射 , 使得 .
3.2商拓扑
定义 3.2.1. 令 为拓扑空间, 为集合, 为一个满射. 则 的关于 的商拓扑 (quotient topology) 定义如下: 的子集 被称为商拓扑下的开集, 当且仅当 是 的开集.
如果赋予 关于映射 的商拓扑, 那么很容易刻画什么样的从 映出的映射是连续的.
命题 3.2.2. 记号如上. 赋予 商拓扑. 令 为拓扑空间. 令 为映射. 则 连续的必要且充分条件是 连续.
定义 3.2.3. 称拓扑空间之间连续映射 为商映射 (quotient map), 如果它是满射, 且 原本的拓扑与关于 的商拓扑一致.
拓扑空间 关于映射 的饱和 (saturated) 子集 是指形如 , 的子集. 映射 为商映射的必要且充 分条件为它是连续满射, 并且将饱和开 (闭) 集映成开 (闭) 集.
3.2.4 (等价关系的商空间). 若 是一个拓扑空间, 为 上的一个等价关系. 则 我们赋予等价类的集合 关于映射 的商拓扑. 这个拓扑叫做 的商拓扑 (quotient topology). 商集 以及其上的商拓扑叫做拓扑空间 关于等价关系 的商空间 (quotient space). 今后若无特别申明, 当我们使用记号 时, 我们总是使用商拓扑.
命题 3.2.5. 令 为拓扑空间 上的等价关系. 令 为商映射. 设 为连续映射, 且满足 . 则存在唯一的连续映射 使得 .
3.3商映射的判据
考虑实数空间 上的等价关系 . 映射的纤维恰好是关系 的等价类. 根据之前的讨论, 我们已经能赋予商空间 商拓扑了. 通过命题 3.2.5, 映射 给出了一个连续的双射 . 我们希望说明 是同胚. 也就是说, 自己原本的拓扑与通过双射 所获得的拓扑一致, 即 自身的拓扑是 的商拓扑. 换言之, 我们必须说明 是一个商映射.
在这一小节里, 我们介绍几个验证映射是商映射的方法.
通过证明截面的局部存在性
首先我们给出一个一般的观察, 它说明 对连续满射来说, 它是 “商映射” 这个性质是一个靶空间上的局部性质 (a property that is local on the target).
命题 3.3.1. 令 为连续满射. 如果 , 且 是开集, 则连续满射 是商映射的必要充分条件是 都是商映射.
命题 3.3.2. 令 为连续映射. 设 拥有一个截面 (section) (即 是一个满足 的连续映射). 则 是商映射.
因此, 如果一个连续映射在靶空间上局部有截面, 它就是一个商映射.
我们可以利用截面来验证小节开始时的映射 为商映射. 整体上, 没有截面. (为什么?) 但是只要我们选择合适的 “主值”, 我们就可以通过反三角函数来用 或者 来决定角度, 从而定义局部截面. 由于余弦函数在开区间 单调, 上半个开圆周上就可以定义连续映射它是 的局部截面. 在下半个开圆周也可以定义 的局部截面类似地, 通过选择反正弦函数的恰当主值就可以在左右开半圆周定义出局部截面. 这样, 就在 局部有截面. 因此它是商映射.
通过证明映射是开映射或闭映射
其次, 按照定义, 连续满射是商映射当且仅当它将饱和开 (闭) 集映成开 (闭) 集. 因此我们有如下结果.
比如, 我们可以通过验证导引里的映射 是开映射来说明它是商映射. 一种验证映射是开映射的方法是利用微分学.
3.3.4 (使用微分学来验证映射是开映射). 设 和 , 其中 , 都是开集, 是 映射, 隐函数定理的一个推论 (所谓的常秩定理) 说, 如果 Jacobi 矩阵 的秩在 上每一点都是 , 那么 是一个开映射. 因此 是商映射.
使用微分学的判据可以验证导言中的 是开映射. 一种计算方法是可以使用球极投影将 同胚地等同于 , 然后计算复合映射的微分, 验证它处处非零. (类似地处理 .) 这个计算留给读者进行.
3.3.5 (利用紧性验证映射是闭映射). 我们将在第 6.1 节介绍紧性. 利用紧性相关的概念可以比较方便地证明映射是闭映射. 我们将证明紧空间到 Hausdorff 空间连续映射是闭映射 (系 6.1.4).
在习题 6.8.13 中, 我们将证明下列闭映射的判据: 如果 是连续映射, 的紧子空间在 下的原像也紧, 且 局部紧 Hausdorff, 那么 是闭映射.
3.4商拓扑的简单例子
1. | 在 上引入等价关系 如下: 当且仅当存在非零实数 , 使得 . 则这个等价关系共有两个不同的等价类 和 . 而这个等价关系的商空间同胚于 Sierpiński 空间 (我们有 ). 因此, Hausdorff 空间的商空间未必是 Hausdorff 的. |
2. | 令 为拓扑空间. 令 为子空间. 引入由 , 生成的等价关系. 所得到的商空间有时记为 . 商映射 将整个子空间 “坍缩” 成了一个点. 比如, 将空间 的子空间 坍缩掉. 此商空间叫做 的锥 (cone). 又比如, 商空间 同胚于 . 事实 上, 映射 诱导了所需的同胚. |
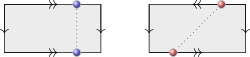
3. | 在研究曲面的时候经常会使用下面这样的示意图: 图 2: 环面与 Klein 瓶 它的意思是将用同一种方法标记的边按照所示方向粘接在一起. 左图粘出了环面, 而右图粘出了所谓的 Klein 瓶. 比如在这两个图中, 虚线边缘所示的点被粘合了, 并且矩形的四个顶点也被粘合了. |
4. | 令 为拓扑空间. 是 的子空间. 令 为连续映射. 我们定义 沿着 的推出 (pushout) (记号: 或者 ) 为 , 其中 是由 , 生成的等价关系. 我们有如下连续映射的交换图 如果 , , 则空间 被称为是往拓扑空间 沿着 安装了一个 维胞腔 得到的空间. 推出满足如下泛性质: 对任何满足 的连续映射 , , 存在唯一的连续映射 使得 , . |
5. | 最后, 我们给出一个例子, 说明商映射的积不一定是商映射. 令 , . 令 为商映射. 令 为坍缩 所得的点. 我们来证明 不是商映射. 令 . 令 是如图 3 所示阴影区域构成的开集. 图 3: 集合 令 . 由于 的第二个坐标是无理数, 是一个饱和开集. 我们断言 不是开集. 如果是, 它就会是 的一个邻域. 因此存在 的邻域 , 和实数 , 使得 . 因此 落在 中. 这与 矛盾. |
3.5粘贴开集
本段里我们讨论如何从小片开始粘合空间. 一组粘贴开集的素材是指如下的数据:
(用什么粘) 一族拓扑空间 , | |||||||
(在哪里粘) 一族开子集 , , 满足 , | |||||||
(怎么粘) 同胚 , 满足下列条件:
|
有了粘贴的素材, 我们引入等价关系来粘贴 . 在集合 上引入关系我们来验证 是一个等价关系. 由于 , 我们有 对任何 成立. 如果 , 则存在 , 使得 . 由于 , 我们有 . 因此关系 是对称的. 最后, 如果 , , 那么存在 , 使得 , 即 . 由此验证了 的传递性.
我们称商空间 为通过开集粘贴素材 粘贴所得的拓扑空间.
命题 3.5.1. 记号如上. 我们有如下结论.
1. | 商映射 是开映射. |
2. | 复合映射 诱导了 与 的同胚, 并且 是 的开子空间. |
3. | 复合映射 诱导了 与 的开集 的同胚. |
证明. 由于开映射可以在定义域上局部检验, 而 是 的开覆盖, 为 了证明第 1 款成立. 我们只需证明, 对任意 , 任意 的开子集 , 是 的开子集. 为此, 根据商空间的性质, 我们要验证饱和集 是 的开集. 由于 的拓扑是空间 的不交并拓扑, 我们需要验证, 对任何 , 是 的开集. 这个集合包含了一切 中的点 , 它与某个 关于 等价. 这些点正好是集合 中的子集 . 根据粘贴素材的定义, 是 的开集, 是 的开集, 所以 是 的开集, 又 是同胚, 因此 是 的开集. 进而它是 的开集.
现实中验证条件 (1) – (3) 会比较繁琐. 一个比较简单的情形如下. 设我们事先已经有了一个集合 , 且 是一些子集的并, 每个 都事先给定了一个拓扑空间结构. 令 , 为恒等映射, 则条件 (1) – (3) 就自动成立. 如果所有 都是 的开集, 那么我们就得到了一个开集粘贴素材.
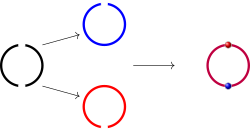
例 3.5.2. 令 , , . 由于只有两片开集, 条件 (3) 是显然的. 因此我们可以将两条实数轴沿着开集 使用恒等映射 粘接起来. 所得到的空间叫做有两个原点的仿射直线 (affine line with double origin) (见图 4). 它不是一个 Hausdorff 空间. 红色的原点的任何邻域一定是蓝色原点的去心邻域.
图 4: 有两个原点的仿射直线
我们也可以用另一种方法来粘合 和 , 我们可以令 . 如果这样粘合的话, 我们得到了 . 见图 5.
图 5: 用两个实轴粘合圆周
具体的商映射可以用南极和北极分别的球极投影给出.
3.6流形
一个 维拓扑流形 (topological manifold) 是指一个具有可数拓扑基的 Hausdorff 拓扑空间 , 它有开覆盖 , 其中每一个 都同胚 于 的开子集. 在这个覆盖中, 同胚 叫做一个图表 (chart)1.
为了构造拓扑流形, 可以使用 的开子集为 作为开集粘贴素材 (这些 叫做 图表 (chart)). 粘贴的时候要小心, 因为有可能会粘出不 Hausdorff 的空间 (比如有两个原点的仿射直线). 一个能够保证粘合空间为 Hausdorff 的条件如下: 对任何 , 要么存在一个 使得 , 要么存在两个不相交的 , , 使得 , . 在下一小节中我们会通过这个方法来说明射影空间是流形.
在粘贴的过程中, 同胚 叫做坐标转移函数. 使用特别的坐标转移函数允许我们定义特殊类别的流形. 如果 是 (或者 ) 的子集, 并且同胚 是可微的 (或复解析的), 那么粘贴所得的流形就叫做微分流形 (differentiable manifold) (或复流形 (complex manifold)). 如果 是 , 而 是仿射映射, 那么粘出来的流形就叫做仿射流形 (affine manifold). 在微分 (复, 仿射) 流形之间可以定义可微 (全纯, 仿射) 映射的概念. 上述结构的存在允许我们使用更多的工具来研究流形, 并且会为流形的拓扑提供特殊的限制.
另一个构造流形的方法是借助下述命题.
命题 3.6.1. 令 为欧氏空间中开集 上一族可微函数 2. 假设 Jacobi 矩阵 在 上每一点的秩都是 . 则 是一个 维流形.
证明. 由于 是度量空间, 它是 Hausdorff 的. 因此 也是 Hausdorff 空间 (命题 2.5.1/(5)). 中坐标为有理数的点的有理半径的球与 的交为 的可数拓扑基, 因此只需对任何 构造一个同胚于 的邻域即可.
读者应该能验证, 上述方式定义的流形实际上是微分流形.
3.7射影空间 (I)
作为集合, 维实射影空间 是一切线性空间 的 1 维线性子空间的全体. 即: 中的一个点, 是 经过原点的一条直线. 我们用符号 来代表经过非零向量 的唯一的 一维子空间. 因此 .
令 是 中不包含在超平面 中的一维子空间的全体. 令则 作为 的子空间同胚于 . 对于任何 中的点 , 与 有唯一的交点. 如果 , 则这个交点为 . 由此定义双射因此, 我们可以通过双射 来赋予 拓扑. 在此拓扑下, 都是 的开集. 如果 是 的坐标, 在 下的像是 中由不等式 (如果 ) 或 (如果 ) 定义的区域.
因此集合 , 伴以 的上述拓扑, 给出了粘贴开集的素材. 我们用此赋予 拓扑. 通过上述构造, 我们能看出 是一个流形 (留给读者检验 Hausdorff 性质). 根据上述定义, 以及例 3.5.2, 我们发现 . 将 换成 , 同样的操作可以给出复射影空间 的拓扑结构.
本节所学概念与例子
- 商映射 quotient map
- 饱和子集 saturated subset
- 等价关系 equivalence relation
- 商集 quotient set
- 代表元 representative
- 商拓扑 quotient topology
- 坍缩 collapse
- 流形 manifold
- 锥 cone
- 推出 pushout
- 胞腔 cell
- 有两个原点的仿射直线 affine line with double origin
- 射影空间 projective space
3.8习题
3.8.1 (闭映射). 设 为拓扑空间之间的连续映射.
1. | 证明下述陈述等价.
满足上述条件的连续映射叫做闭映射 (closed map). | ||||
2. | 举例说明连续映射未必是闭映射. | ||||
3. | 举例说明, 如果 是闭映射, 是拓扑空间, 未必是闭映射. |
3.8.2 (收缩). 令 为拓扑空间 的子空间. 令 为包含映射. 一个从 到 的 收缩 (retraction) 是一个连续映射 , 它满足 . 如果存在从 到子空间 的收缩, 我们称 是 的一个收缩核 (retract).
1. | 收缩是商映射. |
2. | 若 为 Hausdorff 空间, 是 的收缩核, 那么 是 的闭子空间. |
3. | 在 2 中, 去掉 “Hausdorff” 可以吗? |
3.8.3 (截面). 令 为连续映射. 连续映射 叫做 的截面 (section), 如果 .
1. | 令 为 的一个截面. 如果 是非分歧映射 (习题 2.6.4), 那么 是 的开集. |
2. | 令 为 的一个截面. 如果 是分离映射 (习题 2.6.6), 那么 是 的闭集. |
3. | 如果 , , 且 , 则 没有截面. |
3.8.4. 令 为拓扑空间.
1. | 构造一个 Hausdorff 空间 , 它具有一族互不相交的稠密子空间 . |
2. | 设 是第 1 款中所述空间. 证明 是 Hausdorff 空间. |
3. | 证明往 方向的投影在 上的限制 是商映射. 由此推出 M. Shimrat3 的定理: 任何拓扑空间都是某个 Hausdorff 空间的商空间. |
3.8.5. 设 为商映射, 且它的一切纤维都是有限集合. 若 是 Hausdorff 空间, 是否 Hausdorff?
3.8.6 (复射影空间的 Zariski 拓扑). 我们使用 3.7 段的约定 (将 换成 ). 每个 的子集 可以通过一一映射 而获得 的 Zariski 拓扑 (见习题 2.6.7).
1. | 验证诸 的 Zariski 拓扑可以给出粘贴开集的素材, 由此得到了 的不同于通常拓扑的拓扑. 这个拓扑叫做 复射影空间的 Zariski 拓扑. |
2. | 的 Zariski 拓扑同胚于 的 Zariski 拓扑. |
3. | 令 为关于 的齐次多项式. 则对 , 谈论 在点 的值没有意义. (为什么?) 但是我们总可以谈论是否 . 证明 是 Zariski 闭集的必要且充分条件是存在一系列齐次多项式 , 使得 |
4. | 证明 的两个非空 Zariski 开集都相交. |
5. | 的 Zariski 拓扑与 的 Zariski 拓扑不同胚. 4 |
3.8.7. 考虑下图所示的粘贴曲面的示意图.
证明两种示意图给出同胚的曲面.
3.8.8. 我们在球面上取一个线段, 并将球面沿着这个线段 “剖开”. 取两个沿着线段剖开的球面, 见下图, 并沿着剖开的线段粘合. 粘合所得空间是什么?
3.8.9. 设想在我们三维世界 中放一个哆啦 a 梦故事里的 “任意门”, 通过这个门我们可以从我们的世界 “穿越” 到另一个三维世界 (或者我们同一个世界的另一个地点). 你能否用拓扑学的术语描述任意门连接两个世界这个操作?
3.8.10. 设 为拓扑空间, 是它的子空间. 根据商拓扑的泛性质, 锥 有自然的到 的连续单射. 这个单射一定是同胚吗?
脚注
1. | 流形的另一个定义是: 一个 维拓扑流形是一个第二可数 Hausdorff 空间, 每个点都有一个邻域同胚于 . 这个定义似乎比我们上面写的定义强, 但是读者稍微反应一下应该能意识到这两个定义是等价的. |
2. | 再次提醒, 我们的讲义中可微是 的同义词. |
3. | Shimrat, M. (1956). Decomposition spaces and separation properties. Quart. J. Math. 2: 128–129. |
4. | 助教注释: 见 GTM 52, Ch. 1 第 3 节的习题 3.1(d). 一个证明是先做该小节习题 3.5, 再做 3.7(b), 然后考虑 3.7(a). 最后用他们推出 3.1(d). |