用户: Cybcat/高维的Riemann映射定理不成立
1高维的 Riemann 映射定理
我们遵循 Raghavan Narasimhan 的多复变书上的流程来逐步解决这个问题, 同时也算是对 Daniel Huybrechts 第一章相关习题的一个小勘误. 对于一个连通开区域 , 我们用 表示 到自身的全纯自同构构成的群. 在紧开拓扑下我们可以将 看作一个拓扑群.
首先我们回顾 Cartan 的一个重要结果:
命题 1.1 (Cartan). 设 是有界开区域, 全纯且 . 那么 .
推论 1.2. 若 是有界开区域, 满足 推出 . 且现有全纯自同构 使 , 则 是线性映射.
命题 1.3. 记 , 那么 总能被写成如下复合: 首先做坐标置换 , 然后做每个分量保持圆不动的的分式线性变换 .
定理 1.4 (Poincare). 和 不全纯等价.
2Schwarz 引理与像直径
按照传统我们的笔记总是会引入一些和主题可能关系不大的东西, 本次我们要来看 Stein 复变书上的一道习题. 这个问题将一些组合几何与复变联系起来, 而且确实具有一些深刻背景.
[Stein & Shakarchi 复分析, 第 2 章, 习题 7]
假设 全纯, 其中 是单位圆盘. 证明更进一步地, 不等号取等当且仅当 .
首先做一些简单的尝试, 我们马上就会发现, 这个简单的尝试能解决取等以外的问题.
首先很明显要写出 Cauchy 积分公式, 任取 实数, 则在 处导数为然后小技巧就是换元 , 这样 处的导数还能写成二者相加就得到然后写出放缩 , 那么换元 就得知需要在长度为 的圆周上积分. 由此绝对值不等式即得到 . 取 就得到 .
然而证明取等的部分却异常艰辛, 请觉得简单的读者自行尝试.
实际上, 这个形式已经非常接近 Schwarz 引理, 所以我们要做的第一步就是套用之. 下面为了行文简便, 用 来代替 而不改变问题, 故可假设 以及 , 那么此时 . 现在考虑 也就是前文分子出现过的形式.
Schwarz 引理的想法是这样的, 此时 , 同时在 圆周上, , 那么根据最大模原理, 我们知道 在整个 中全纯而且模长不超过 , 而且由于在点 处取到 , 有取等就必须有 常值, 故 . 这意味着 是一个偶函数, 但是截至这里, 我们对其系数仍一无所知.
那么很自然地, 我们就会思考 是不是一个反例呢? 很可惜并不是, 让我们来展示 时边界的形状, 只需代入 便得到这样的图案:
从图上看很直观, 该图案与虚轴的截距已经超过 . 实际上这里有奇妙的平面几何, 该图案在平面直角坐标系的方程应为如果用 代替 , 原先的方程就变成代入 解得两个平凡零点以外还有这实则意味着过原先图案的 点的任意弦长度都为定值 . 某种意义上说该图形和圆也非常相似, 只是没有将过圆心的弦的中点固定下来罢了. 实际上 这条弦恰好就经过 . 这是因为
问题出在哪呢? 我们意识到最大的距离并不是经过 的弦 , 如果我们形式地考虑带增量的也就是说, 假如 在单位圆上, 那么为了保证微微扰动 后不会超模, 结合 是纯虚数, 必须要有 是实数. 这意味着 在单位圆周上取 , 但是 全纯所以只能有 是常数.
回归主线, 怎么将上述证明严谨化呢? 对 , 考虑一个辅助函数 , 现在它在单位圆周上就是光滑的. 而且也有 , 此时我们就应当考虑 , 依定义现在对给定的 , 由于 是全纯函数, 所以根据最大模原理, 在 的模长最值关于 是一个单调不减的函数, 这表明 是一个关于 单调不减的函数. 这启发我们看 , 幂级数展开即可注意到 没有常数项, 随着 它的高次项 (二次开始) 都过快消失, 因此在 上一致收敛到其一次项 . 这表明 , 结合单调性, 我们得知 恒成立. 这样用 代替 即可使用前一段的论证技术. 具体来说, 现在函数在 的一个邻域内全纯性得知了.
于是任意取定 定义 求导得到等于 是因为 已经取到直径, 从而不能更大.
于是利用前面得到的 整理表达式可知 对任意 . 使用 Schwarz 反射技巧 (例如先把 全纯等价为上半平面 , 然后使用共轭的函数延拓下半平面, 就得到全平面的有界全纯函数) 可知 是常函数, 因此 在单位圆内恒成立, 这表明 , 结论得证.
3中场休息: 两个构造性破题
例 3.1. 试构造具体的双全纯映射, 将单连通区域 打到上半平面.
这个形状是复平面扣掉了射线 以及线段 . 直接构造关于它的映射并不容易. 那么技巧是这样的.
首先考虑 , 也就是原本区域在上半平面的部分. 我们先思考怎么把它映射到上半平面? 方法很简单, 注意到 会将上半平面的缝和边界变成平行的, 这时 的像为 . 于是再作 , 它就变成上半平面 . 换言之, 我们用 将 变到 .
现在我们回到 的研究去, 那么我们为什么要研究 呢, 实际上, 我要强调 可以将定义域从 解析延拓到 去!
具体来说, 我们使用 Schwarz 反射原理. 注意到原本 可以延拓到 去, 这样一来, 它被映到射线 . 所以根据反射原理, 我们可以将 延拓到 上. 总结一下, 此时的效果是, 将 映射到上半平面 ; 将 映到射线 ; 将 映到下半平面 . 于是 的像是 . 这时再经过 即可打到 .
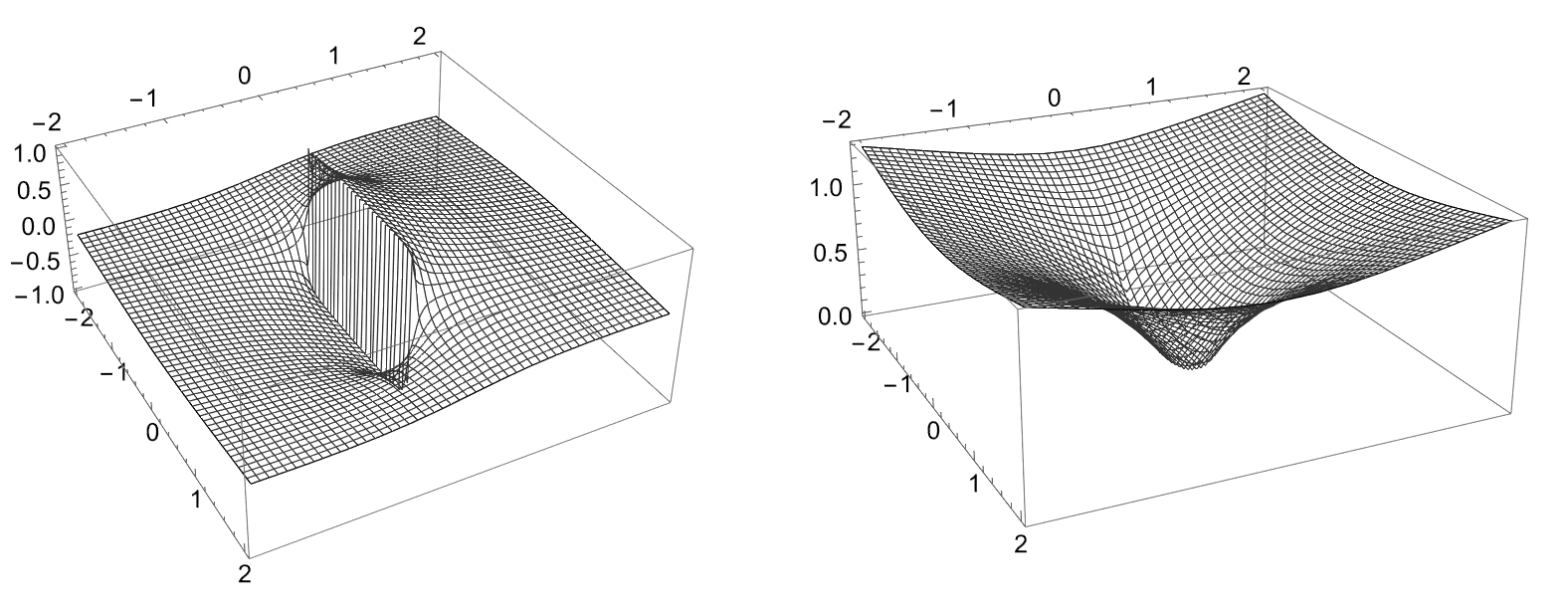
例 3.2. 试构造一个 上连续的函数 , 满足它仅在 上调和.
此事其实极其简单, 利用 Poisson 公式, 我们可以在上半平面构造这样的边值问题的解, 在 轴上为 . 然后在下半平面我们构造以 为边值的解. 现在积分得到上半平面: 有趣的是我们算出的这个上半 的形式恰好在下半平面就是 边值的解. 所以换言之这个 在全平面除了 外调和, 有界, 而且在这个线段两侧跳跃. 现在我们只需计算积分 即可得到符合题意的解. 经计算, 我们有读者如果感兴趣, 可以运行下面的 mathematica 代码来绘制图像:
Plot3D[(ArcTan[(1 - x)/y] + ArcTan[(1 + x)/y])/Pi, {x, -2, 2}, {y, -2, 2}, PlotRange -> All, PlotStyle -> None, MaxRecursion -> 4, Mesh -> 50]
Plot3D[(2 y (ArcTan[(1 - x)/y] + ArcTan[(1 + x)/y]) - (-1 + x) Log[(-1 + x)^2 + y^2] + (1 + x) Log[(1 + x)^2 + y^2])/( 2Pi), {x, -2, 2}, {y, -2, 2}, PlotRange -> All, PlotStyle -> None, MaxRecursion -> 4, Mesh -> 50]