用户: Cybcat/曲线模空间/JS第三讲
1第三讲
光滑曲线与节点曲线
有了前面的铺垫, 现在我们可以定义代数曲线的模函子了. 不过如常, 我们快速过一遍背景介绍.
以后我们说曲线时, 一概地谈论一个符合上述条件的复曲线. 另外讨论的范畴和概形也限制在 -概形范畴 中.
命题 1.3. 对于光滑不可约射影曲线 .
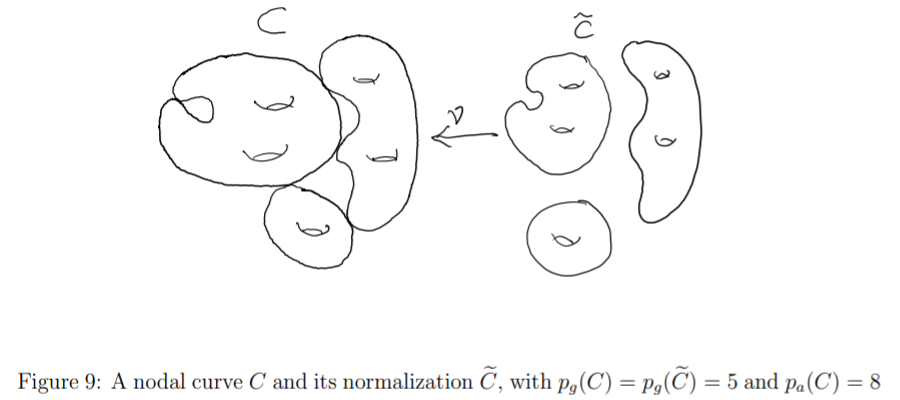
例 1.4. 对节点曲线 , 我们有 . 注意它的正规化是 .
注 1.5. 黎曼面说明. 我们叙述一些关于曲线和黎曼面间的对应事实, 光滑射影 (一维时等价于紧合) 曲线在解析拓扑下对应紧黎曼面, 反过来, 紧黎曼面也一定是射影代数曲线, 我不想介绍一般的 GAGA. 这里有一个来自 Griffiths & Harris 的证明, 只使用了标准的工具: Kodaira 消失定理. 当然一些黎曼面的书上会使用来自 Riemann–Roch 定理的更具体的计算.
基本的想法无非是寻找 上的线丛 能区分点以及一个点处的切向量, 这样它的整体截面给出嵌入 . 注意到 区分点 当且仅当存在整体截面的满射 . 而我们有短正合列计算上同调可知, 整体截面满射当且仅当 , 实际上 Kodaira 消失定理告诉我们只需 时, 这就总成立. 然后对切向量我们也可以使用完全一样的方法, 只不过研究 .
最后周定理告诉我们射影空间中的闭曲线都是代数的. 为了写这句话, 周定理的页面就是我写的.
现在拥有解析化后的好处是不言而喻的, 不仅能合理地用拓扑解释什么是亏格, 还能具体地用复流形的模空间理论来帮助我们思考. 另一方面, 亏格对二维紧拓扑流形来说是一个同胚下的完善分类 (闭曲面分类定理), 这里就能清晰地看出刚性对于流形起到了怎么样的限制.
接下来我们严谨地定义节点:
定义 1.6. 设 是复曲线, (闭) 点 称为一个节点, 是指以下等价条件被满足:
(1)(解析簇看法) 存在邻域 使得局部上它解析同构 的零点集.
(2)(代数簇看法) 局部环 的完备化是 .
定义 1.7. 一个节点曲线指的是每个 (闭) 点处要么光滑, 要么为节点的曲线.
假设 是复射影节点曲线 的正规化, 那么经过逐点地检查: 在 的光滑处 是同构映射, 在 的节点处 会分裂成两个点, 所以有正规化正合列由此我们得到节点曲线的亏格公式:
推论 1.8.
这里我试图插入一幅原书中的图片, 它绘制了正规化在黎曼面的表现, 非常具有代表性.
比较准确的描述是, 节点曲线从它的正规化得来的方法, 对应将一些 " 甜甜圈 " 上的点对粘接起来. 例如 , 写成 , 其上的点可以被 参数化, , 原点以外都有唯一的 对应, 唯独原点有 两个原像. 这样完备化 (射影化) 后会将 上的两个点 粘起来, 连同复结构, 在局部上就形如 .
几何亏格就不考虑这种 " 通过粘接点对得到的不完全的洞 ", 但是代数亏格会考虑, 你可以在左图中数出 个这种 " 洞 ".
此外还有一些有趣的事情, 当曲线在形变的时候, 回忆我们前面的例子 Legendre 族椭圆曲线. 我们意识到这过程中节点会产生, 代数亏格总保持不变 , 几何亏格却会变. 看起来我们要用代数亏格来作为讨论的基础了, 但很快就会意识到, 代数亏格 的节点曲线确实太多了, 因为我们可以通过结点给它粘上很多个 , 使得它的模空间看起来就不大是紧的. 马上就会发现, 这其实又是自同构惹的祸.
正确的研究对象, 实则是带有若干标记点的稳定曲线.
自同构的引入
定义 1.9. 一个复射影, 连通的节点曲线 , 在满足如下条件时被称 为稳定的: 进一步地, 给定 上的点 . 在满足如下条件时被称 为稳定的:
我们还是来速通一下关于黎曼面的自同构理论.
定理 1.10. 不可约光滑复射影曲线 , 设其亏格为 . 那么:
(1) 若 则 且 .
而且这一作用是 -传递的. 对互不相同的 , 存在唯一的自同构把它们映到 .
(2) 若 则 是椭圆曲线, .
其中 之一, 取决于格的对称性. 即借助加法结构简单平移, 所以是 -传递的.
(3) 若 则 有限, 阶被 控制.
(1), (2) 和 (3) 分别是标准的 Mobius 变换理论, 椭圆曲线理论, Hurwitz 定理.
推论 1.11. 设 是不可约光滑复射影曲线, 亏格 , 其上不同的 个点 , 我们有
那么让我们鼓起勇气处理节点曲线的情形:
定理 1.12. 是连通复射影节点曲线. 假设 是互不相同的光滑点, 则 稳定当且仅当正规化 的每个不可约分支 皆满足: 这里 即其亏格, 表示 以及节点 (这两类点通称特殊点) 中位于 上者的数量.
从这个定理我们就能看出前面那个通过结点粘很多个 的构造会破坏稳定性. 虽说它不改变亏格, 但是它带来了很多神秘的自同构.
光滑稳定曲线族与模空间
现在我们终于可以定义曲线族的概念. 而且, 从模空间理论的哲学 (philosophy) 上看, 我们需要给曲线标记一些点. 一般地, 我们也要同时处理好光滑曲线族和稳定曲线族.
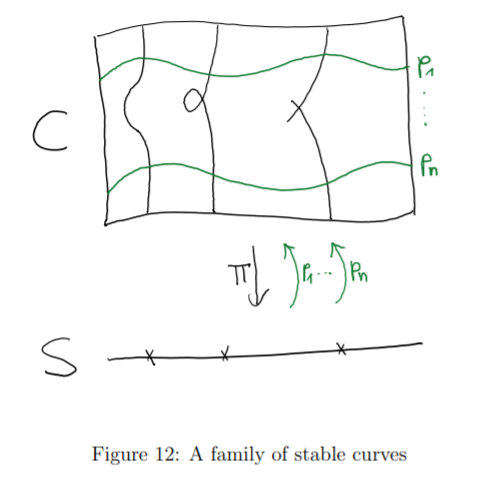
定义 1.13. 给定 , 一个被概形 参数化的, 带 个标记点的, (光滑/稳定) 亏格 曲线族包含如下资料: 常简称一族 (光滑/稳定) 曲线, 满足如下条件:
是 (光滑/平坦), 紧合, 满, 有限表现的概形态射; 使得每个几何点上的纤维 都是一个 (光滑/稳定), 射影, 连通曲线, 算术亏格 .
态射 是 两两不交的截面, 像坐落在 光滑之处 (smooth locus).
两个这样的族等价指的是存在 -同构 , 使得 . 使得如下的图表交换:
另外对映射 , 可以自然地定义 沿 的拉回, 记 为纤维积 以及诱导的截面 .
总的来说, 这些概念还是很自然的, 原书上一幅直观的示意图如下:
注 1.14. 关于上述定义有一些补充事实:
(a) 若 比较合理, 例如它满足局部诺特的条件, 那么紧合自然推出有限表现. 有限表现的具体作用我们会在下面的 (c) 处提到.
(b) 我们要求每个纤维都是射影曲线, 这看起来应该用某种更好的说法取代, 例如直接说态射 射影. 但是这会带来一些技术困难, 比如说射影当然不能局部检查, 不过对于我们的定义, 对一族稳定曲线来说 局部射影. 大概的思想是考虑 对应的典范丛 , 在每个纤维 上丰沛, 代数几何上 (参见 EGA IV) 就得知这个线丛是 -相对丰沛的, 这就对应着局部射影性.
(c) 我们对 平坦的要求也有些可说的. 光滑当然推出平坦, 对稳定族来说, 由代数几何的结论 [平坦紧合局部有限型] 推出 [欧拉示性数是局部常值的] . 使得即便我们不在定义中提出, 在 的连通分支上可自然得到了相同的 .
终于, 我们可以正确地定义模函子 :
定义 1.15. 模函子 的定义, 它将概形 映到对概形态射 , 诱导的集合映射由拉回给出. 不难检查拉回的函子性.
让我们先看一看 (但是不证) 大定理应该有的样子:
定理 1.16 (Deligne–Mumford–Knudsen). 假设非负整数 满足 , 那么:
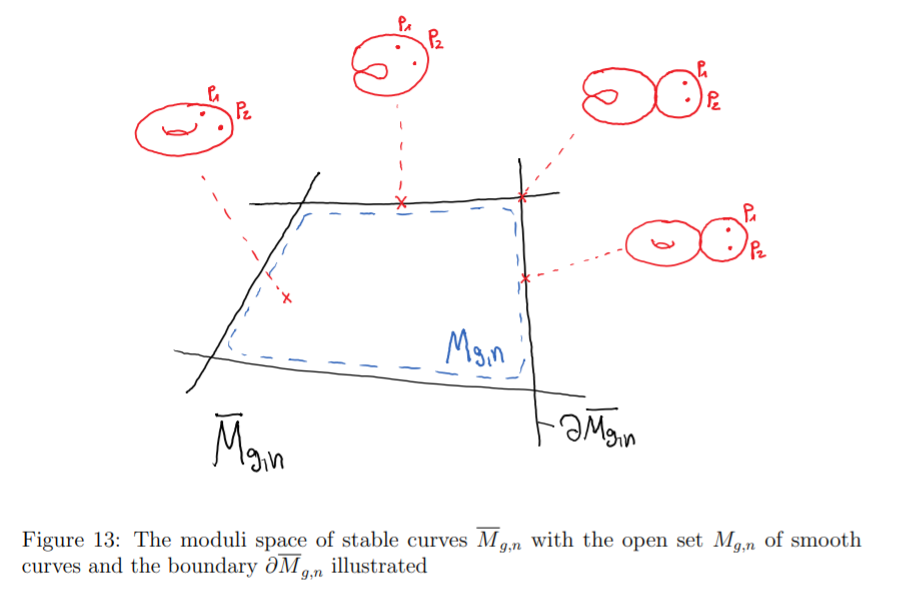
(a) 存在 的粗模空间 .
(b) 是正规 代数簇, 维数为 . 而且存在自然开浸入 像集稠密.
(c) 簇 不可约, 射影而且具有商奇点 (quotient singularities).
所谓商奇点, 就是其奇点局部上形如 , 其中 光滑仿射, 是有限群.
(d) 边界 是一个 Weil 除子. 实际上它一般不是 Cartier 的, 不过因为它具有商奇点, 它是 -factorial 的, 所以它的一个倍数是 Cartier 除子.
(e) 最后, 考虑 为使得下式成立的那些带标记点曲线 (的等价类) 构成的子簇: 那么 是光滑开子簇, 而且它是 的精模空间: 这个函子即在稳定曲线族定义中加入自同构平凡. 于是它有万有族, 由下面的交换图表示.
原书作者手绘了如下的模空间示意图:
注 1.17. 注意到条件 就是为了保证存在足够多的光滑曲线稳定, 以至于不发生 . 实际上最后寄掉的也就是非常有限的这么几种情况: 而注意到定理中的 (e) 部分, 实际上 时, 当且仅当以后我们会对此作更多的说明, 不过就现在来说, 至少一方面说告诉我们这两件事: 对于 " 绝大多数 " 的带 个标记点椭圆曲线和亏格 曲线, 其自同构群非平凡. 椭圆曲线带一个标记点, 实则相当于交换的扭子 (torsor) 标记了幺元, 它在取群逆元下自同构. 至于亏格 曲线, 通过考虑典范丛 我们知道它总是 超椭圆曲线, 换言之总存在 的双页分歧覆盖 (次数 ). 所以这诱导了二次扩张 , 故 存在一个仿射开集对应 对某多项式 . 这样就应当是自然的对合, 更简单地说, 因为二次扩张都是 Galois 扩张, 所以这将带来 的非平凡 (对合) 自同构. 有趣的是, 人们通过分类, 实则知道 的自同构无非只能是以下情况: 其中的 分别是 和 的某些二重覆盖. 不过一般的 , 我们只有 , 它是三维的因为 . 其他的情况维数比较低, 是二维的, 是一维的, 剩下三种情况甚至是唯一的. 形状上类似椭圆曲线的经典两样:
另外比较幸运的是 . 我们其实有类似 -不变量的概念区分亏格 超椭圆曲线. 其中记 是五次单位根则 这样作用: 不多说了.
为了能让读者更好地理解这一大定理, 我们将在下一讲中介绍很多具体的低亏格情形. 此外, 我们不仅会引入更多的重要概念, 还会在繁多的例子中找到证明大定理的蛛丝马迹.