我们现在可以对紧区间 I
假设 I = [ a , b ] − ∞ < a < b < + ∞ f : I → R
1)
f ∈ R ( I )
2)
存在常数 I ε > 0 δ > 0 ( σ , ξ ) ∈ S ′ ( I ) ∣ σ ∣ < δ ∣ ∣ S ( f ; σ , ξ ) − I ∣ ∣ < ε .
3)
f D ( f ) = D ( f )
4)
f ∫ a b f = ∫ a b f
当上面的任意一个条件成立时, 我们就有D ( f ) = D ( f ) = ∫ a b f = ∫ a b f = ∫ a b f .
证明. 1)⇒ 19.1 I ∫ a b f
2)⇒ ε > 0 δ ∣ σ ∣ < δ ( σ , ξ ) ∣ S ( f ; σ , ξ ) − I ∣ < ε σ 0 = { b 0 < b 1 < ⋯ < b 0 } ∣ σ 0 ∣ < δ
我们令 ξ i = a i , i = i 0 ξ i 0 = x ∈ [ a i 0 − 1 , a i 0 ] ∣ S ( f ; σ , ξ ) ∣ < I + ε ∣ ( a i 0 − a i 0 − 1 ) f ( x ) ∣ ⩽ ∣ ∣ i = i 0 ∑ ( a i − a i − 1 ) ∣ ∣ ∣ f ( ξ i ) ∣ + ∣ S ( f ; σ , ξ ) ∣ ⩽ ∣ ∣ i = i 0 ∑ ( a i − a i − 1 ) ∣ ∣ ∣ f ( a i ) ∣ + I + ε . x f [ a i 0 − 1 , a i 0 ] I
现在令 m i = x ∈ [ a i − 1 , a i ] inf f ( x ) ζ i ∈ [ a i − 1 , a i ] m i ⩽ f ( ζ i ) ⩽ m i + b − a ε S ( f ; σ , ζ ) S ( f ; σ , ζ ) ⩽ S ( f ; σ ) + ε ⩽ D ( f ) + ε . I ⩽ D ( f ) + 2 ε . I ⩾ D ( f ) − 2 ε . ϵ → 0 D ( f ) = D ( f )
3)⇔ 19.3
4)
⇒ 1) 根据上下极限的定义, 对任意的
ε > 0 , 存在两个阶梯函数
f ( x ) 和
f ( x ) , 使得
f ( x ) ⩾ f ( x ) ⩾ f ( x ) , 并且
0 ⩽ ∫ a b f ( x ) − ∫ a b f ( x ) < ε . 从而, 我们令
F ( x ) = f ( x ) 和
ψ ( x ) = f ( x ) − f ( x ) ∈ E ( I ) , 我们自然有
∣ f ( x ) − F ( x ) ∣ ⩽ ψ ( x ) , ∫ a b ψ < ε . 这说明
f ∈ R ( I ) . 另外, 我们自然有
∫ a b f ⩽ ∫ a b f ⩽ ∫ a b f , 这就证明定理中要求的积分的等式.
我们已经建立了比较完备的积分理论, 下面我们要发展一个最基本的工具来联系积分与微分并以此进行计算. 先引入原函数的概念: 假设 f I I f I F F F ′ = f F f 原函数 . 假设 F f f { F + c ∣ ∣ c ∈ R }
对任意的 f ∈ R ( I ) x ∈ I F ( x ) = ∫ a x f f [ a , x ] F ( x ) I = [ a , b ] f x 0 F x 0 f ( x 0 + ) = h → 0 , h > 0 lim f ( x 0 + h ) f ∈ C ( I ) F ( x ) = ∫ a x f ( y ) d y f
证明. 首先证明 F ∈ C ( I ) ∣ f ∣ ⩽ M x ∈ I h > 0 ∣ F ( x − h ) − F ( x ) ∣ = ∣ ∣ − ( ∫ a x f − ∫ a x − h f ) ∣ ∣ = ∣ ∣ ∫ x − h x f ∣ ∣ ⩽ ∣ h ∣ × M = O ( h ) . F x F x F ( a ) = 0
进一步假设
f 在
x 0 处右连续, 令
f ( x 0 + ) 为
f 在
x 0 处的右极限, 即
f ( x 0 + ) = h → 0 + lim f ( x 0 + h ) . 按定义, 对任意的
ε , 存在
δ > 0 , 使得当
h ∈ ( 0 , δ ) 时, 我们有
∣ f ( x 0 + h ) − f ( x 0 + ) ∣ < ε . 据此, 我们计算
∣ F ( x 0 + h ) − F ( x 0 ) − f ( x 0 + ) h ∣ = ∣ ∣ ( ∫ a x 0 + h f − ∫ a x 0 f ) − f ( x 0 + ) h ∣ ∣ = ∣ ∣ ∫ x 0 x 0 + h ( f ( x ) − f ( x 0 + ) ) d x ∣ ∣ ⩽ ε h . 由于
ε 是任意选取的, 所以
F ( x 0 + h ) − F ( x 0 ) − f ( x 0 + ) h = o ( h ) . 这表明,
f ( x 0 + ) 是
F 在
x 0 处的右导数.
假设 f ∈ C ( I ) F ( x ) = ∫ a x f ∈ C 1 ( I ) F ′ = f F f
假设 I f ∈ R ( I ) f F ∫ a b f = F ( x ) ∣ ∣ a b . F ( x ) ∣ ∣ a b = F ∣ ∣ x = a x = b = F ( b ) − F ( a )
证明. 我们注意到, 如果 f ∈ C ( I ) F ( b ) = ∫ a b f , F ′ = f . F ( a ) = 0 F ∈ C 1 ( I )
现在考虑一般情况: 我们要证明, 对任意的 ε > 0 ∣ F ( b ) − F ( a ) − ∫ a b f ∣ < ε . f ∫ a x f ( y ) d y F ( x ) = ∫ a x f ( y ) d y [ − 1 , 1 ] [ − 1 , 1 ] → R , x ↦ { x 2 sin ( x 2 1 ) , 0 , x = 0 ; x = 0.
根据 f g , ψ ∈ E ( I ) ∣ f ( x ) − g ( x ) ∣ ⩽ ψ ( x ) , ∀ x ∈ I ; ∫ a b ψ < ε . σ = { a = a 0 < ⋯ < a n = b } g ψ g ψ ( a i − 1 , a i ) y i = g ∣ ∣ ( a i − 1 , a i ) , z i = ψ ∣ ∣ ( a i − 1 , a i ) .
为了控制
∣ ∣ F ( b ) − F ( a ) − ∫ a b f ∣ ∣ , 我们自然考虑它较好的一个逼近:
F ( b ) − F ( a ) − ∫ a b g = i = 1 ∑ n ( F ( a i ) − F ( a i − 1 ) ) − i = 1 ∑ n ∫ a i − 1 a i g = i = 1 ∑ n ( F ( a i ) − F ( a i − 1 ) − ( a i − a i − 1 ) y i ) = i = 1 ∑ n ( ( F ( a i ) − a i y i ) − ( F ( a i − 1 ) − a i − 1 y i ) ) . 在每个区间
[ a i − 1 , a i ] 上, 我们考虑函数
x ↦ F ( x ) − y i x . 根据 Lagrange 中值定理, 存在
ξ i ∈ [ a i − 1 , a i ] , 使得
∣ ∣ ( F ( a i ) − a i y i ) − ( F ( a i − 1 ) − a i − 1 y i ) ∣ ∣ = ∣ ∣ F ′ ( ξ i ) − y i ∣ ∣ ( a i − a i − 1 ) = ∣ ∣ f ( ξ i ) − g ( ξ i ) ∣ ∣ ( a i − a i − 1 ) ⩽ ψ ( ξ i ) ( a i − a i − 1 ) = z i ( a i − a i − 1 ) . 所以, 我们得到
∣ ∣ F ( b ) − F ( a ) − ∫ a b g ∣ ∣ ⩽ i = 1 ∑ n z i ( a i − a i − 1 ) = ∫ a b ψ < ε . 最终, 我们有
∣ ∣ F ( b ) − F ( a ) − ∫ a b f ∣ ∣ ⩽ ∣ ∣ F ( b ) − F ( a ) − ∫ a b g ∣ ∣ + ∣ ∣ ∫ a b ( f − g ) ∣ ∣ ⩽ ε + ∫ a b ψ < 2 ε 令
ε → 0 , 我们就证明了微积分基本定理.
Newton-Leibniz 公式最常用的形式是: f ∈ C 1 ( I ) ∫ a b f ′ = f ( x ) ∣ ∣ a b .
给定一个函数 f ∫ f f f F F ′ = f f
我们罗列几个基本的原函数: ∫ x α = α + 1 1 x α + 1 , α = − 1 ; ∫ x 1 = log x ; ∫ log x = x log x − x ; ∫ sin x = − cos x ; ∫ cos x = sin x ; ∫ e x = e x ; ∫ a 2 + x 2 1 = a 1 arctan a x ; ∫ a 2 − x 2 1 = arcsin a x ; ∫ tan a x = − a 1 log cos a x . ∫ sec x = log ∣ sec x + tan x ∣ = 2 tanh − 1 ( tan 2 x ) ; ∫ sec 2 a x = a tan a x ; ∫ csc x = log ∣ tan 2 x ∣.
我们将会看到, 关于原函数的计算 (如果可以用初等函数表示的话) , 本质上是代数的变形, 所以, 我们需要记忆并熟练的运用以上几个例子.
这些例子的证明是平凡的, 我们只需要对原函数求导来验证它恰好给出了所求的函数即可. 利用 Newton-Leibniz 公式和上面的原函数, 我们可以计算很多积分了:
1)
单项式的积分: ∫ a b x n = n + 1 1 x n + 1 ∣ ∣ a b = n + 1 1 ( b n + 1 − a n + 1 ) .
2)
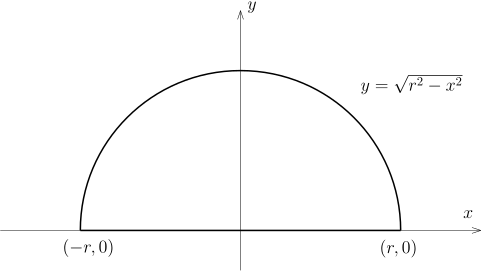
π = π 2 r 2 π
这就是函数 f ( x ) = r 2 − x 2 x ∈ [ − r , r ] ∫ − r r f = ∫ − r r r 2 − x 2 . r 2 − x 2
作为 Newton-Leibniz 公式应用, 我们现在来证明分部积分公式和变量替换公式.
假设 f , g ∈ C 1 ( I ) ∫ a b f ′ ⋅ g = ( f ⋅ g ) ∣ ∣ a b − ∫ a b f ⋅ g ′ .
证明. 对
( f ⋅ g ) ′ 用 Newton-Leibniz 公式, 所以
( f ⋅ g ) ∣ ∣ a b = ∫ a b ( f ⋅ g ) ′ = ∫ a b f ′ ⋅ g + ∫ a b f ⋅ g ′ . 这自然等价于分部积分公式.
我们回忆一下所谓的 Abel 求和公式: 假设 { a k } k ⩾ 1 { b k } k ⩾ 1 k = 1 ∑ n a k b k = S n b n + k = 1 ∑ n − 1 S k ( b k − b k + 1 ) , S n = a 1 + a 2 + ⋯ + a n { a k } k ⩾ 1 S k b k Z ⩾ 1 S k ⟶ f , b k ⟶ g , Z ⩾ 1 ⟶ [ a , b ] ,
假设 Φ : I → J I = [ a , b ] J = [ c , d ] f ∈ C ( J ) I α < β ∫ α β ( ( f ∘ Φ ) ⋅ Φ ′ ) = ∫ Φ ( α ) Φ ( β ) f .
证明. 我们先假设
Φ ( β ) > Φ ( α ) . 根据
f ∈ C ( I ) 和
Φ ∈ C 1 ( I ) , 我们知道上面两个积分的被积函数都是连续的, 所以都是 Riemann 可积的. 根据复合函数求导公式, 令
F ( x ) 为
f ( x ) 的一个原函数, 那么我们有
F ( Φ ( x ) ) ′ = f ( Φ ( x )) Φ ′ ( x ) ⇔ ( F ∘ Φ ) ′ = ( f ∘ Φ ) ⋅ Φ ′ . 所以利用 Newton-Leibniz 公式, 我们有
∫ α β ( f ∘ Φ ) ⋅ Φ ′ = ∫ α β ( F ∘ Φ ) ′ = F ∘ Φ ∣ ∣ α β = F ( Φ ( β )) − F ( Φ ( α )) . 另外, 由于
f ( x ) 是连续的, 所以我们可以选取
F 为
F ( x ) = ∫ a x f . 从而,
F ( Φ ( β )) − F ( Φ ( α )) = ∫ a Φ ( β ) f − ∫ a Φ ( α ) f = ∫ Φ ( α ) Φ ( β ) f . 命题得证.
注意到, 我们假设了 Φ ( α ) < Φ ( β ) I = [ a , b ] ∫ I f ∫ a b f a < b ∫ a b ∫ α β ( f ∘ Φ ) ⋅ Φ ′ = F ( Φ ( β )) − F ( Φ ( α )) Φ ( β ) < Φ ( α ) ∫ Φ ( α ) Φ ( β ) f ∫ Φ ( α ) Φ ( β ) f = − ∫ Φ ( β ) Φ ( α ) f = − ( F ( Φ ( α )) − F ( Φ ( β )) ) ∫ a b f = − ∫ b a f .
作为换元积分公式的推论, 我们证明两个基本的命题. 尽管这两个命题的证明不值一提, 但是由于下面的平移和相似变换是
R 上最基本的对称性 (共形变换群) , 所以它们占有特殊的位置:
•
假设 f ∈ R ( I ) g ( x ) = f ( x + x 0 ) g = f ∘ τ x 0 : [ a − x 0 , b − x 0 ] → R τ x 0 : [ a − x 0 , b − x 0 ] → [ a , b ] x ↦ x + x 0 ∫ a − x 0 b − x 0 g = ∫ a b f .
•
假设 f ∈ R ( I ) λ > 0 g ( x ) = f ( λ x ) g = f ∘ m λ : [ λ a , λ b ] → R m λ : [ λ a , λ b ] → [ a , b ] x ↦ λ x λ ∫ λ a λ b g = ∫ a b f .
根据变量替换公式的形式, 我们倾向于将积分写成传统的形式: ∫ a b f ( x ) d x
为了讲的更清楚, 我们回忆微分 (不是导数! ) 的定义. 给定一个两个区间之间的可微的映射 Φ : X → Y x 0 ∈ X T x 0 X ≃ R y 0 ∈ Y T y 0 Y ≃ R Φ x 0 d Φ ( x 0 ) : T x 0 X → T Φ ( x 0 ) Y , h ↦ Φ ′ ( x 0 ) h . X = Y Φ x ↦ x x Φ ′ = 1 d x ( x 0 ) : T x 0 X → T Φ ( x 0 ) X , h ↦ h . T x 0 X → T Φ ( x 0 ) Y d Φ ( x 0 ) = Φ ′ ( x 0 ) d x ( x 0 ) . d Φ = Φ ′ ( x ) d x . y Φ ( x ) y = Φ ( x ) ∫ α β f ( Φ ( x ) ) d Φ ( x ) Φ ′ ( x ) d x = ∫ Φ ( α ) Φ ( β ) f ( y ) d y .
我们可以看一下如何利用分部积分和换元积分公式进行积分的计算. 在一定的意义上, 这已经不属于分析的范畴了 (不用取极限或者
ε 语言) , 而算是组合或者是代数上的操作了:
我们先来完成关于圆的面积的计算:
1)
我们用如下的变量替换 x = r sin θ Φ : [ − 2 π , 2 π ] → [ − r , r ] ∫ − r r r 2 − x 2 d x = ∫ − 2 π 2 π r 2 − ( r sin θ ) 2 r cos θ d θ = r 2 ∫ − 2 π 2 π ( cos θ ) 2 d θ = 2 r 2 ∫ − 2 π 2 π ( cos ( 2 θ ) + 1 ) d θ = 2 r 2 ( ∫ − 2 π 2 π cos ( 2 θ ) d θ + π ) = ϑ = 2 θ 2 r 2 ( 2 1 ∫ − π π cos ( ϑ ) d ϑ + π ) sin x sin ( π ) = sin ( − π ) ∫ − π π cos ( ϑ ) d ϑ = sin ϑ ∣ ∣ − π π = 0. ∫ − r r r 2 − x 2 d x = 2 r 2 π . r π r 2 π = π π π
2)
计算 ∫ 0 2 3 π sin 2 x cos x d x ∫ 0 2 3 π sin 2 x cos x d x = ( ∫ 0 2 π + ∫ 2 π π + ∫ π 2 3 π ) sin 2 x d sin x = ∫ 0 1 y 2 d y − ∫ 0 1 y 2 d y − ∫ − 1 0 y 2 d y = 3 1 − 3 1 − 3 1 = − 3 1 . Φ ( β ) < Φ ( α )
3)
计算 ∫ 0 2 π x sin x cos x d x x ∫ 0 2 π x sin x cos x d x = 2 1 ∫ 0 2 π x sin ( 2 x ) d x = − 4 1 ∫ 0 2 π x ( cos ( 2 x ) ) ′ d x = 4 1 ∫ 0 2 π cos ( 2 x ) d x − 4 1 x cos ( 2 x ) ∣ ∣ 0 2 π = 8 1 ∫ 0 2 π ( sin ( 2 x ) ) ′ d x + 8 1 π = 8 1 π .
4)
计算 ∫ 1 2 x 1 + x 2 1 d x x y 1 ∫ 1 2 x 1 + x 2 1 d x = ∫ 2 1 1 1 + y 2 1 d y . ∫ 1 + x 2 1 = log ( x + 1 + x 2 ) ∫ 2 1 1 1 + y 2 1 d y = log 1 + 5 2 + 2 2 . 1 + x 2 y = sinh z ∫ 2 1 1 1 + y 2 1 d y . = ∫ α β cosh z 1 cosh z d z = β − α , sinh ( α ) = 2 1 sinh ( β ) = 1 α β