给定区域 Ω 上的 m-次微分算子 P 和分布 u∈D′(Ω), 假设 Pu=f 是光滑的, 那么, WF(u)⊂Z(σm(P)),其中, Z(σm(P)) 是 P 的主象征的零点集. 我们现在要进一步刻画 WF(u) 的几何结构, 这就是所谓的奇性传播定理.
我们先引入一些定义:
给定区域 Ω 上的 m-次微分算子 P, 我们把Char(P):=Z(σm(P))⊂T∗Ω=Ω×Rn称作是 P 的特征簇 (characteristic variety) .
给定 (x0,ξ0)∈Char(P), 如果 pm(x,ξ)=σm(P) 在 (x0,ξ0) 的一个邻域上是实值的并且 ∇x,ξpm(x0,ξ0) 与 (ξ0,0) 是线性无关的, 我们就称 Char(P) 在 (x0,ξ0) 处是简单的, 也称 P 在 (x0,ξ0) 处具有简单特征.
如果 P 在每个 Char(P) 上的点处都是简单的, 我们就称 P 具有简单的特征簇.
假设微分算子 P 具有简单的特征簇, 那么, 对每个 (x0,ξ0)∈Char(P), pm(x,ξ) 在 (x0,ξ0) 处的微分不是 0, 这说明 Char(P)⊂T∗Ω 是光滑子流形 (余维数为 1) .
之前, 我们按照如下的方式定义了主特征: 如果P=∣α∣⩽m∑pα(x)∂α,那么, pm(x,ξ)=σm(P)(x,ξ)∣α∣=m∑pα(x)(−iξ)α.从此之后, 因为有上述关于 pm(x,ξ) 是实值的要求, 我们令pm(x,ξ)=σm(P)(x,ξ)=∣α∣=m∑pα(x)(ξ)α.这对之前的证明没有影响.
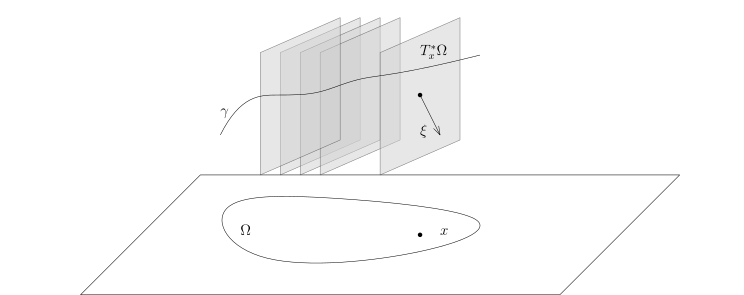
给定区域 Ω 上的 m-次微分算子 P, 我们假设它的象征 pm(x,ξ) 是实数值的函数, 那么如下定义的 T∗Ω 上的向量场HP=(∂ξ1∂pm,⋯,∂ξn∂pm,−∂x1∂pm,⋯,−∂ξn∂pm)被称作是 P 所定义的 Hamilton 向量场. 形式上, 我们经常把这个向量场写成HP=(∂ξ∂pm,−∂x∂pm).我们通常把 H(x,ξ)=pm(x,ξ) 称作是 T∗Ω 上的一个 Hamilton 作用量.
假设
γ:(−a,b)→T∗Ω是过
(x0,ξ0)∈T∗Ω 的
Hp 的一条积分曲线, 其中
a,b>0. 这指的是
γ(t)=(x1(t),x2(t),⋯,xn(t),ξ1(t),ξ2(t),⋯,ξn(t))并且
⎩⎨⎧x1′(t)x2′(t)xn′(t)ξ1′(t)ξ2′(t)ξn′(t)γ(0)=∂ξ1∂pm(x1(t),⋯,xn(t),ξ1(t),⋯,ξn(t)),=∂ξ2∂pm(x1(t),⋯,xn(t),ξ1(t),⋯,ξn(t)),⋯⋯=∂ξn∂pm(x1(t),⋯,xn(t),ξ1(t),⋯,ξn(t)),=−∂x1∂pm(x1(t),⋯,xn(t),ξ1(t),⋯,ξn(t)),=−∂x2∂pm(x1(t),⋯,xn(t),ξ1(t),⋯,ξn(t)),⋯⋯=−∂xb∂pm(x1(t),⋯,xn(t),ξ1(t),⋯,ξn(t)),=(x0,ξ0). 在上面这个图中, 我们把每个点
x∈Ω 处的
{x}×Rn 记作是
Tx∗Ω. 我们经常把这个方程组简写成
⎩⎨⎧x′(t)ξ′(t)γ(0)=∂ξ∂pm(x(t),ξ(t)),=−∂x∂pm(x(t),ξ(t)),=(x0,ξ0).关于 Hamilton 向量场, 我们有如下熟知的性质:
Hamilton 作用量 pm(x,ξ) 沿着 HP 的积分曲线是常数, 即对任意的 Hp 的积分曲线γ:(−a,b)→T∗Ω,我们有dtd(pm(x(t),ξ(t)))=0.
证明. 我们只要利用
γ 的方程进行计算即可:
dtd(pm(x(t),ξ(t)))=∂x∂pm(x(t),ξ(t))x′(t)+∂ξ∂pm(x(t),ξ(t))ξ′(t)=∂x∂pm(x(t),ξ(t))∂ξ∂pm(x(t),ξ(t))+∂ξ∂pm(x(t),ξ(t))(−∂x∂pm(x(t),ξ(t)))=0.命题成立.
假设
γ 是
HP 的一条积分曲线, 如果
γ∩Char(P)=∅, 根据上面的引理, 那么,
pm 在
γ 的每个点上的取值都是
0, 所以,
γ⊂Char(P).
我们把落在 Char(P) 中的 HP 的极大的一条积分曲线称作是微分算子 P 的一条双特征曲线 (bicharacteristics) .
有了双特征曲线的概念, 我们就可以陈述奇性传播定理了:
给定区域 Ω 上的 m-次微分算子 P, 我们假设 P 具有简单的特征簇. 如果 γ 是 P 的一条双特征曲线并且γ∩WF(Pu)=∅,其中 u∈D′(Ω) 是分布, 那么如下两种情形必居 (且只居) 其一:
算子 P 是区域 Ω 上的 m-次微分算子并且具有简单的特征簇, u∈D′(Ω) 是分布. 如果 Pu 是光滑的, 那么 WF(u) 是双特征曲线的无交并.
为了证明这个定理, 我们先做一番准备. 我们定义相函数ϕ(s,x,ξ):R×T∗Ω→R.这是一个对于 ξ 是 1 次齐次的函数, 它由如下的常微分方程所定义: ⎩⎨⎧∣ξ∣m−1∂s∂ϕ(s,x,ξ)=−pm(x,∇xϕ(s,x,ξ)),ϕ(0,x,ξ)=x⋅ξ.其中, m 为 P 的次数. 特别地, 由于 ϕ 对于 ξ 的次数为 1, 所以, ϕ 可以被下面的方程刻画: ⎩⎨⎧∂s∂ϕ(s,x,ξ)=−pm(x,∇xϕ(s,x,ξ)),ϕ(0,x,ξ)=x⋅ξ,其中, ξ∈Sn−1. 这是因为pm(x,∇xϕ(s,x,ξ))=pm(x,∇xϕ(s,x,∣ξ∣ξ)∣ξ∣)=∣ξ∣mpm(x,∇xϕ(s,x,∣ξ∣ξ)).
利用相函数 ϕ(s,x,ξ), 我们可以刻画双特征曲线:
假设 γ(t)=(x(t),ξ(t)) 是 P 的一条双特征曲线, 那么, 对任意的 t∈R, 我们有ξ(t)=(∇xϕ)(t,x(t),ξ0),其中, γ(0)=(x0,ξ0).
我们定义
ζ(t)=(∇xϕ)(t,x(t),ξ0).很明显,
ζ(0)=∇x(x⋅ξ0)=ξ0=ξ(0).我们将证明, 对任意的
t, 我们都有
ξ(t)=ζ(t).证明. 假设
∣ξ∣=1, 我们考虑
ζ(t) 所满足的微分方程:
ζ′(t)=∂t∂x∂2ϕ(t,x(t),ξ0)+∂x2∂2ϕ(t,x(t),ξ0)x′(t).利用方程, 我们有
∂t∂x∂2ϕ(t,x(t),ξ0)=−∂x∂pm(x,∂x∂ϕ(t,x(t),ξ0))−∂ξ∂pm(x,∂x∂ϕ(t,x(t),ξ0))∂x2∂2ϕ(t,x(t),ξ0).所以,
ζ′(t)=−∂x∂pm(x(t),ζ(t))+矩阵乘法∂x2∂2ϕ(t,x(t),ξ0)⋅[x′(t)−∂ξ∂pm(x(t),ζ(t))]另外, 根据定义, 我们还有
⎩⎨⎧x′(t)ξ′(t)=∂ξ∂pm(x(t),ξ(t)),=−∂x∂pm(x(t),ξ(t))..所以,
ζ′(t)−ξ′(t)=−[∂x∂pm(x(t),ζ(t))−∂x∂pm(x(t),ξ(t))] −∂x2∂2ϕ(t,x(t),ξ0)⋅[∂ξ∂pm(x(t),ζ(t))−∂ξ∂pm(x(t),ξ(t))].根据 Lagrange 中值定理 (我们用到了
pm 是光滑函数并且其导数在
γ 附近是有界的) , 我们就有
∣ζ′(t)−ξ′(t)∣⩽C∣ζ(t)−ξ(t)∣.由于
∣ζ(t)−ξ(t)∣∣∣t=0=0,上面的微分不等式表明
ζ(t)≡ξ(t).命题得证.
利用微分方程的解对初始值的光滑依赖性以及紧性, 我们有如下的推论:
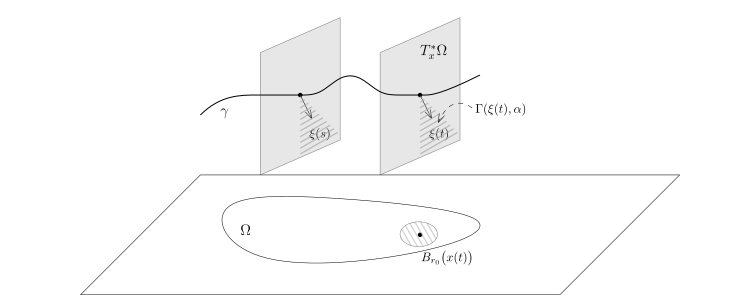
我们考虑一段双特征曲线γ:[0,t0]→T∗Ω.对任意给定 α0>0, 存在 r0>0 和 β>0, 使得对任意的 t∈[0,t0], 对任意的 (x,ξ)∈Br0(x(t))×Γ(ξ(t),β), 我们都有∂x∂ϕ(t,x,ξ)∈Γ(ξ(t),α0).
证明. 对任意的
t∈[0,t0], 根据引理
84.7, 上述关系对于
(x(t),ξ(t))∈Br0(x(t))×Γ(ξ(t),β) 成立, 利用连续性, 就对
Br0(x(t))×Γ(ξ(t),β) 中所有的点都成立. 由于所有可能的
t 所给出的
{Br0(x(t))×Γ(ξ(t),β)} 是
γ 的开覆盖, 利用紧性, 我们就得到了结论.
奇性传播定理的证明: 条件
我们首先把条件γ∩WF(Pu)=∅,用分析的语言写清楚.
对任意的 t⩽t0, γ(t)=(x(t),ξ(t))∈/WF(Pu), 从而, 存在 ψ0(x)∈C0∞(Ω), α(t)>0, 使得 ψ0 在 x(t) 附近恒为 1 并且对任意的 N>0, 存在 CN, 对任意的 ξ∈Γ(ξ(t),2α(t)), 我们有∣∣ψ0⋅Pu(ξ)∣∣⩽(1+∣ξ∣)NCN.所以, 对任意的 φ∈C0∞(Br(t)(x(t))) (半径 r(t) 很小) , 其中 ψ0∣∣Br(t)(x(t))=0, 对任意的 ξ∈Γ(ξ(t),α(t)), 我们有∣∣φ⋅Pu(ξ)∣∣=∣F(φ⋅ψ0Pu)(ξ)∣⩽(1+∣ξ∣)NCN′∣μ∣⩽M(N)sup∥∂μφ∥L∞.最后的一步, 我们用了引理 82.3, 其中, M(N) 是依赖于 N 的常数. 当 t 遍历 [0,t0] 时 (我们可以假设 t0=1) , 我们知道 Br(t)(x(t))×Γ(ξ(t),α(t)) 覆盖了 γ([0,1]), 所以, 我们可以选出有限个 t1,⋯,tl, 使得γ⊂j⩽l⋃Br(tj)(x(tj))×Γ(ξ(tj),α(tj)):=Γ(γ).所以, 存在 r0>0 和 α0>0, 对任意的 t∈[0,1], Br0(x(t))×Γ(ξ(t),α0)⊂Γ(γ). 特别地, 根据 Lebesgue 数的存在性 (第一学期第 11 次课) , 对任意的 t, Br0(x(t))×Γ(ξ(t),α0)xi∈Γ(ξ(t),α0) 必然落在某个 Br(tj)(x(tj))×Γ(ξ(tj),α(tj)) 中 (这里我们可以先在 Ω×Sn−1 这个紧集上考虑) . 通过选取最小的 CN 和最大的 M(N), 我们就得到了如下的结论:
存在 r0>0 和 α0>0, 对任意的 t∈[0,1], 使得对任意的 N>0, 存在常数 CN 和 MN, 使得对任意的 φ∈C0∞(Br0(x(t))), 对任意的 ξ∈Γ(ξ(t),α0), 我们有∣∣φ⋅Pu(ξ)∣∣⩽(1+∣ξ∣)NCN∣μ∣⩽MNsup∥∂μφ∥L∞.
我们不妨假设 γ(1)∈/WF(u), 我们只要说明在另一个端点处 γ(0)∈/WF(u) 即可. 我们先在翻译 γ(1)∈/WF(u) 这个条件: 存在 r1>0 和 α1>0, 对任意的 N>0, 存在常数 CN 和 MN, 使得对任意的 φ∈C0∞(Br1(x(1))), 对任意的 ξ∈Γ(ξ(1),α1), 我们有∣φ⋅u(ξ)∣⩽(1+∣ξ∣)NCN∣μ∣⩽MNsup∥∂μφ∥L∞.
作为总结 (缩小 r0 和 r1 等) , 我们把奇性传播定理的条件总结如下:
存在 r0>0 和 α0>0, 对任意的 t∈[0,1], 使得对任意的 N>0, 存在常数 CN 和 MN, 使得
• | 对任意的 φ∈C0∞(Br0(x(t))), 对任意的 ξ∈Γ(ξ(t),α0), 我们有∣∣φ⋅Pu(ξ)∣∣⩽(1+∣ξ∣)NCN∣μ∣⩽MNsup∥∂μφ∥L∞. |
• | 对任意的 φ∈C0∞(Br0(x(1))), 对任意的 ξ∈Γ(ξ(1),α0), 我们有∣φ⋅u(ξ)∣⩽(1+∣ξ∣)NCN∣μ∣⩽MNsup∥∂μφ∥L∞. |
奇性传播定理的证明: 拟解的构造
我们需要计算如下形式的导数: −eiϕ(∣ξ∣m−1i∂t∂+tP)(e−iϕc)假设 c(t,x,ξ) 是阶为 d, 那么, 我们要将上面的式子写成三个部分, 第一个部分的阶为 d+m, 第二个部分的阶为 d+m−1, 第二个部分的阶 ⩽d+m−2.
我们令 Q=tP, 那么Qf=tPf=∣α∣⩽m∑qα(x)∂αf(x)=∣α∣⩽m∑(−1)α∂α(pα(x)⋅f(x)).利用归纳法, 我们不难证明, 对任意的多重指标 μ, 我们有eiϕ∂μ(e−iϕ)=∣μ1∣⩾1,⋯,∣μl∣⩾1μ1+⋯+μl=μ,∑(−1)l∂μ1ϕ⋅∂μ2ϕ⋯∂μlϕ.所以, eiϕtP(e−iϕc)=eiϕ∣α∣⩽m∑qα(x)∂α(e−iϕc)=∣α∣⩽m∑μ⩽α∑(μα)qα(x)eiϕ∂μ(e−iϕ)∂α−μc=∣α∣⩽m∑μ⩽α∑μ1+⋯+μl=μ,∣μj∣⩾1∑(−1)l(μα)qα(x)(∂μ1ϕ⋯∂μlϕ)∂α−μc.在这个表达式中, 每个 ∂μjϕ(t,x,ξ) 对于 ξ 都是 1 次的, 所以, 上面所出现的关于 ξ 的最高阶项是 d+m 阶的, 最低阶项是 d 阶的. 我们下面将对不同的阶数进行合并同类项.
• | d+m 阶项. 此时, 我们必须有 l=∣μ∣=∣α∣=m, 所以, 这些项为===∣α∣=m∑(−1)mμ1+⋯+μm=α∑qα(x)(∂μ1ϕ⋯∂μlϕ)c∣α∣=m∑(−1)mqα(x)(∂x∂ϕ)αc(t,x,ξ)∣α∣=m∑(−1)mqα(x)(∂x∂ϕ)αc(t,x,ξ)pm(x,∂x∂ϕ)⋅c(t,x,ξ). |
• | d+m−1 阶项. 此时, 我们必须有 l=m−1. 所以, ∣μ∣⩾m−1. ∘ | 如果 ∣μ∣=m, 此时, ∣α∣=m, 所以, 这些项为=∣μ∣=m∑μ1+⋯+μm−1=μ∑(−1)m−1qμ(x)(∂μ1ϕ⋯∂μlϕ)cMϕ,P⋅c(t,x,ξ).这里, Mϕ,P(t,x,ξ)=∣μ∣=m∑μ1+⋯+μm−1=μ∑(−1)m−1qμ(x)(∂μ1ϕ⋯∂μlϕ)对于 ξ 是一个次数为 m−1 的齐次函数, 它的构造只依赖于 ϕ 和 pm (主象征! ) . | ∘ | 如果 ∣μ∣=m−1. 我们定义多重指标 δj=(0,⋯,0,1,0,⋯,0), 其中只有在第 j 个位置是 1. 这些项为∣α∣⩽m∑μ⩽α,∣μ∣=m−1∑(−1)m−1(μα)qα(x)(∂x∂ϕ)μ∂α−μc.如果 ∣α∣=m−1, 这一类的项可以合并到上面的一项中 (此时, 我们要对 Mϕ,P(t,x,ξ) 进行修正, 它的构造变得依赖于 ϕ 和 P) . 所以, 除去这些项之外, 此时没有处理的项形如=∣α∣=m∑j=1∑n(−1)m−1(α−δjα)qα(x)(∂x∂ϕ)α−δj∂δjcij=1∑n∂ξj∂pm(x,∂x∂ϕ)∂xj∂c. |
|
综上所述, 我们就有eiϕtP(e−iϕc)=d+m次pm(x,∂x∂ϕ)⋅c+d+m−1次Mϕ,P⋅c+ij=1∑n∂ξj∂pm(x,∂x∂ϕ)∂xj∂c+c⩽d+m−2,其中, c⩽d+m−2(t,x,ξ) 是一些次数不超过 d+m−2 次的齐次函数的 (有限) 线性组合.
利用这个公式, 我们就有==−eiϕ(∣ξ∣m−1i∂t∂+tP)(e−iϕc)−∣ξ∣m−1i∂t∂c−∣ξ∣m−1∂t∂ϕc−pm(x,∂x∂ϕ)⋅c−Mϕ,P⋅c−ij=1∑n∂ξj∂pm(x,∂x∂ϕ)∂xj∂c−c⩽d+m−2i1(∣ξ∣m−1∂t+j=1∑n∂ξj∂pm(x,∂x∂ϕ)∂xj)c−=0, 根据ϕ的定义(∣ξ∣m−1∂t∂ϕ+pm(x,∂x∂ϕ))c−Mϕ,P⋅c−c⩽d+m−2.所以, −eiϕ(∣ξ∣m−1i∂t∂+tP)(e−iϕc)=i1L(c)+Mϕ,P⋅c+c⩽d+m−2,其中, L=∣ξ∣m−1∂t+j=1∑n∂ξj∂pm∂xj.作为总结, 我们有
假设 c(t,x,ξ) 是关于 ξ 为 d 次齐次的光滑函数, 那么, 我们有−eiϕ(∣ξ∣m−1i∂t∂+tP)(e−iϕc)=i1L(c)+i1Mϕ,P⋅c+c⩽d+m−2,其中, L(c) 是 d+m−1 次的, Mϕ,P 是次数为 m−1 的齐次函数 (只依赖于 ϕ 和 P) .
我们注意到 ϕ 的构造方式恰好消去了上面可能出现的 d+m 次的项.
对给定的正数 (r0,α0), 存在 ρ0>0, 使得 ρ0<r0 并且如下成立:
对任意的 φ∈C0∞(Bρ0(x(0))), 存在函数序列{bk(t,x,ξ)}k⩾0, {Rk(t,x,ξ)}k⩾0⊂C∞([0,1]×B(x(t),r0)×Γ(ξ(t),α0)),
• | bk(t,x,ξ) 对于 ξ 是次数为 −k 的齐次函数并且对任意的 t 和 ξ, 如果 x∈/B(x(t),r0), 那么 bk(t,x,ξ)=0; |
• | Rk(t,x,ξ) 是有限个次数不超过 m−k−2 的齐次函数 (对于 ξ) 的和并且对任意的 t 和 ξ, 如果 x∈/B(x(t),r0), 那么 Rk(t,x,ξ)=0; |
• | 我们令ak(t,x,ξ)=j=1∑kbj(t,x,ξ).那么, 我们有⎩⎨⎧−ieiϕ∣ξ∣m−1∂t∂(e−iϕak)=eiϕ⋅tP(e−iϕak)+Rk,ak(0,x,ξ)=φ(x). |
证明. 我们归纳地来构造. 先考虑 k=0 的情形. 此时, 我们定义 b0(t,x,ξ) 为如下 (常) 微分方程的解: {L(b0)+Mϕ,P⋅b0=0,b0(0,x,ξ)=φ(x).那么, b0 对于 ξ 是 0 次的齐次函数 (可以先对 ∣ξ∣=1 来解, 然后进行齐次的扩张) .
假设对于 ⩽k 的指标 j, 我们已经构造了 bj, 那么, 我们考虑=−ieiϕ∣ξ∣m−1∂t∂(e−iϕ(ak+bk+1))−eiϕ⋅tP(e−iϕ(ak+bk+1))Rk+(L(bk+1)+Mϕ,P⋅bk+1)+c≤d+m−2.其中 d 为 bk+1 的次数.
由归纳假设,
Rk 是次数不超过
m−k−2 的齐次函数的线性组合, 我们假设它的
m−k−2 次分量为
Rk(m−k−2). 那么, 我们令
{L(bk+1)+Mϕ,P⋅bk+1=−Rk(m−k−2),bk+1(0,x,ξ)=0.那么,
d=−(k+1), 从而
c≤d+m−2 的次数不超过
m−k−3. 这就完成了证明.
奇性传播定理的证明: 完成
我们对方程∂t∂(e−iϕak)=i∣ξ∣1−m⋅tP(e−iϕak)+i∣ξ∣1−me−iϕRk对 t 从 0 到 1 积分, 由于 ϕ(0,x,ξ)=x⋅ξ, 我们就得到e−ix⋅ξφ(x)=e−iϕ(1,x,ξ)ak(1,x,ξ)−i∣ξ∣1−m∫01tP(e−iϕ(t,x,ξ)ak(t,x,ξ))dt −i∣ξ∣1−m∫01e−iϕ(t,x,ξ)Rk(t,x,ξ)dt.所以, 我们有φ⋅u(ξ)=⟨u,e−ix⋅ξφ(x)⟩=⟨u,e−iϕ(1,x,ξ)ak(1,x,ξ)⟩−i∣ξ∣1−m∫01⟨u,tP(e−iϕ(t,x,ξ)ak(t,x,ξ))⟩dt −i∣ξ∣1−m∫01⟨u,e−iϕ(t,x,ξ)Rk(t,x,ξ)⟩dt=H(ξ)⟨u,e−iϕ(1,x,ξ)ak(1,x,ξ)⟩−i∣ξ∣1−m∫01I(ξ,t)⟨Pu,e−iϕ(t,x,ξ)ak(t,x,ξ)⟩dt −i∣ξ∣1−m∫01J(ξ,t)⟨u,e−iϕ(t,x,ξ)Rk(t,x,ξ)⟩dt.我们逐一地控制上面的三项:
• | 控制 H(ξ). 首先, 由于 ak(t,x,ξ) 对于 x∈/B(x(t),r0) 是消失的, 所以, 我们可以用一个示性函数 χ(x) 来记住这个事实 (它在 B(x(1),r0) 上恒为 1) : H(ξ)=⟨u,e−iϕ(1,x,ξ)χ(x)ak(1,x,ξ)⟩=∫Rne−iϕ(1,x,ξ)ak(1,x,ξ)χ(x)u(x)dx. 我们选取相函数 ϕ(1,x,ξ), 振幅函数 ak(1,x,ξ) 以及被作用函数 f(x)=χ⋅u(x), 我们来验证它们满足非驻相法引理的基本数据的条件: (a) | ϕ(1,x,ξ)∈C∞(Rxn×(Rξn−{0})) 是实值的, 变量 ξ 是 1 次齐次的并且当 ξ=0 时, 有 ∇xϕ(1,x,ξ)=0: 为了说明后者, 我们用 ϕ(t,x,ξ) 满足的方程: ⎩⎨⎧∂s∂ϕ(s,x,ξ)=−pm(x,∇xϕ(s,x,ξ)),ϕ(0,x,ξ)=x⋅ξ,其中 ∣ξ∣=1. 对 x 求导数, 我们就有∂s∂x∂2ϕ(s,x,ξ)=−∂x∂pm(x,∇xϕ(s,x,ξ))−F(s,x,ξ)∂ξ∂pm(x,∇xϕ(s,x,ξ))∂x2∂2ϕ(s,x,ξ).所以, ∣∣(∂s∂+F∂x∂)∂x∂ϕ∣∣=∣∣−∂x∂pm(x,∇xϕ(s,x,ξ))∣∣⩽C∣∣∂x∂ϕ∣∣m.如果 ∇xϕ(1,x,ξ)=0, 上述微分不等式表明 ∇xϕ(0,x,ξ)=ξ=0, 矛盾! 上面的推理对于 t=1 也成立. | (b) | 按照构造, 对于任意的 t, bj(t,x,ξ) 光滑, 所以 ak(t,x,ξ) 也光滑. 另外, ak(t,x,ξ) 是一些次数不超过 0 的齐次函数的和, 利用紧性, 使得对任意的多重指标 α, 存在常数 Cα, 我们都有∣∂xαak(t,x,ξ)∣⩽Cα. | (c) | 由于 (x(1),ξ(1))∈/WF(u), 对任意的 N⩾1, 存在常数 CN, 使得对任意的 ξ∈Γ(ξ(1),β), 都有我们就有∣∣f(ξ)∣∣⩽(1+∣ξ∣)NCN.这里, η0=∣ξ(1)∣ξ(1). |
根据推论 84.8 以及连续性, 对任意的 (x,ξ)∈B(x(1),r0)×Γ(ξ(1),α0), 我们有∣∣∣∇xϕ(x,ξ)∣∇xϕ(x,ξ)−η0∣∣<β.所以我们可以运用非驻相法引理, 从而, 此时, 引理的结论表明, 对任意的 N⩾1, 存在 CN>0, 使得对任意的 Γ(ξ(0),α0), 有∣H(ξ)∣⩽(1+∣ξ∣)NCN. |
• | 控制 I(ξ,t). 这一部分的控制和 H(ξ) 是完全一致的, 唯一的不同在于把 u 换成了 Pu. 另外, 我们可以对 t 一致地选取 χ. 重复上面的过程, 我们就得到对任意的 N⩾1, 存在 CN>0, 使得对任意的 Γ(ξ(0),α0), 有∣I(ξ,t)∣⩽(1+∣ξ∣)NCN. |
• | 控制 J(ξ,t). 利用分布的定义, 存在常数 C0, 使得, ∣J(ξ,t)∣⩽Cx∈Br0(x(t))∣α∣⩽M,sup∣∣∂α(e−iϕ(t,x,ξ)Rk(t,x,ξ))∣∣. Rk(t,x,ξ) 是有限个 ξ 的次数 ⩽m−k−2 的齐次函数的和, 所以, 根据 Leibniz 法则 (以及 ϕ 对 ξ 的次数为 1) , 上面右端出现的是一些次数不超过 m−k−2+M 的齐次函数的和. 利用 Rk 的光滑性, 我们知道存在常数 CM, 使得(x,ξ)∈Br0(x(t))×Sn−1∣α∣⩽M,sup∣∂αRk(t,x,ξ)∣⩽CM.所以, ∣J(ξ,t)∣⩽(1+∣ξ∣)k+2−M−mCM′,其中, k 是任意的正整数. |
综合上面的所有估计, 我们就证明了对任意的 N⩾1, 存在 CN>0, 使得对任意的 Γ(ξ(0),α0), 有∣φ⋅u(ξ)∣⩽(1+∣ξ∣)NCN.这说明 (x0,ξ0)∈/WF(u), 从而完成了奇性传播定理的证明.