82. 波前集的定义与基本性质

我们知道一个分布的光滑性是一个局部的性质. 给定一个分布 $u\in {\mathcal{D}}^{\prime }(\Omega )$, $u$ 在 $x_0\in \Omega$ 处附近是光滑当且仅当对任意的支集在 $x_0$ 附近的光滑函数 $f$, 我们有 $f\cdot u\in C_0^{\infty }({\mathbb{R}}^n)$. 进一步, $u$ 在 $x_0\in \Omega$ 处附近是光滑当且仅当对某一个任意的支集在 $x_0$ 附近的光滑函数 $f$, $f(x_0)\ne 0$, 我们有 $f\cdot u\in C_0^{\infty }({\mathbb{R}}^n)$. 从 Fourier 分析的角度来看, 函数的光滑性等价于它在频率空间上的衰减. 实际上, 根据 Sobolev 嵌入定理 (或者直接证明) , 在我们刚刚谈论的场合下, 如下两个论述显然是等价的:

1)	$f\cdot u\in C_0^{\infty }({\mathbb{R}}^n)$;
2)	对任意的正整数 $N⩾1$, 存在常数 $C_N$, 使得对任意的 $\xi \in {\mathbb{R}}^n$, 我们有$$\left|\widehat{fu}(\xi )\right|⩽\frac{C_N}{{\left(1+|\xi {|}^2\right)}^{\frac{N}{2}}}.$$

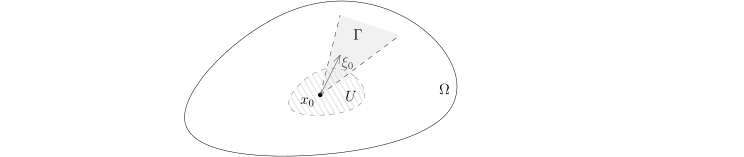
我们现在考察一个特殊的例子: $u=1_{x_n⩾0}$. 这是半空间 ${\mathbb{H}}^n$ 上的示性函数. 它在 $x_n>0$ 或者 $x_n<0$ 上显然是光滑的. 在 $x_n=0$ 这个集合上, 尽管 $u$ 不光滑, 我们发现沿着 $x_1,\cdots ,x_{n_1}$ 的方向求导数总是可以的, 唯一不光滑 (连续) 的方向实际上是变量 $x_n$ 造成的. 我们下面要引入一个概念, 它不仅能说明函数在一个点处不光滑, 而且能说明这个函数沿着哪些方向不光滑.

我们通常用所谓的锥型集来标记方向的集合:

定义 82.1. $\Gamma \subset {\mathbb{R}}_{\xi }^n$ 是频率空间中的一个子集, 如果下面的两个性质成立:

1)	对任意的 $\lambda >0$, 对任意的 $\xi \in \Gamma$, 我们有 $\lambda \cdot \xi \in \Gamma$;
2)	$\Gamma \cap {\mathbf{S}}_{\xi }^{n-1}$ 是 ${\mathbf{S}}_{\xi }^{n-1}$ 上的开集 (闭集) . 这里, ${\mathbf{S}}_{\xi }^{n-1}$ 是频率空间 ${\mathbb{R}}_{\xi }^n$ 中的单位球面.

那么, 我们就称 $\Gamma$ 是一个锥型开集 (闭集) .

另外, 为了方便起见, 我们引入如下的记号: $${\left(T^{\ast }\Omega \right)}^{\times }=\{(x,\xi )\in \Omega \times {\mathbb{R}}^n|\xi \ne 0\}.$$我们现在引入波前集的概念, 目的是说明分布沿着哪些方向不光滑:

定义 82.2. $\Omega \subset {\mathbb{R}}^n$ 是开集, $u\in {\mathcal{D}}^{\prime }(\Omega )$ 是 $\Omega$ 上的分布. 给定 $(x_0,{\xi }_0)\in {\left(T^{\ast }\Omega \right)}^{\times }$, 假设存在开集 $U\subset \Omega$, 锥型开集 $\Gamma \subset {\mathbb{R}}_{\xi }^n$ 以及 $f\in C_0^{\infty }(\Omega )$, 使得

1)	$x_0\in U$, $\mathrm{supp}(f)\subset U$ 并且 $f(x_0)\ne 0$;
2)	${\xi }_0\in \Gamma$;
3)	对任意的正整数 $N⩾1$, 存在常数 $C_N$, 使得对任意的 $\xi \in \Gamma$, 我们有$$\left|\widehat{fu}(\xi )\right|⩽\frac{C_N}{{\left(1+|\xi {|}^2\right)}^{\frac{N}{2}}}.$$

我们就称 $(x_0,{\xi }_0)$ 不落在 $u$ 的波前集里. 我们用 $WF(u)$ 表示不满足上述要求的 $(x_0,{\xi }_0)\in {\left(T^{\ast }\Omega \right)}^{\times }$ 的点的集合. 按照定义, 我们知道$$WF(u)\subset {\left(T^{\ast }\Omega \right)}^{\times }.$$

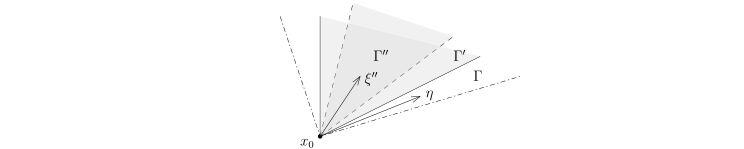
引理 82.3. 给定锥型开集 $\Gamma \subset {\mathbb{R}}_{\xi }^n$, $s_0>0$ 和 $u\in H^{-s_0}({\mathbb{R}}^n)$. 如果对任意的锥型闭集 ${\Gamma }^{\prime }\subset \Gamma$, 对任意的正整数 $N⩾1$, 存在常数 $C_N$, 使得对任意的 ${\xi }^{\prime }\in {\Gamma }^{\prime }$, 我们有$$\left|\hat{u}({\xi }^{\prime })\right|⩽\frac{C_N^{\prime }}{{\left(1+|{\xi }^{\prime }{|}^2\right)}^{\frac{N}{2}}}.$$那么, 对任意的 $f\in C_0^{\infty }(\Omega )$ ($\approx$ 物理空间的任意截断函数) , 对任意的锥型闭集 ${\Gamma }^{\prime \prime }\subset \Gamma$, 对任意的正整数 $N⩾1$, 存在常数 $C_N^{\prime \prime }$, 使得对任意的 ${\xi }^{\prime \prime }\in {\Gamma }^{\prime \prime }$, 我们有$$\left|\widehat{fu}({\xi }^{\prime \prime })\right|⩽\frac{C_N^{\prime \prime }}{{\left(1+|{\xi }^{\prime \prime }{|}^2\right)}^{\frac{N}{2}}}.$$

证明. 选定 $f\in C_0^{\infty }(\Omega )$ 和锥型闭集 ${\Gamma }^{\prime \prime }\subset \Gamma$, 根据 ${\Gamma }^{\prime \prime }$ 在 ${\mathbf{S}}^{n-1}$ 上的闭性, 存在锥型闭集 ${\Gamma }^{\prime }\subset \Gamma$, 使得 ${\Gamma }^{\prime \prime }\subset \mathring{{\Gamma }^{\prime }}$ (落在 ${\Gamma }^{\prime }$ 的内部) . 我们计算 $\widehat{fu}({\xi }^{\prime \prime })$: $$\begin{array}{rl}\widehat{fu}({\xi }^{\prime \prime })& =\frac{1}{(2\pi {)}^n}{\int }_{{\mathbb{R}}^n}\hat{f}({\xi }^{\prime \prime }-\eta )\hat{u}(\eta )d\eta \\ & =\underset{I}{\underbrace{\frac{1}{(2\pi {)}^n}{\int }_{{\Gamma }^{\prime }}\hat{f}({\xi }^{\prime \prime }-\eta )\hat{u}(\eta )d\eta }}+\underset{II}{\underbrace{\frac{1}{(2\pi {)}^n}{\int }_{{\mathbb{R}}^n-{\Gamma }^{\prime }}\hat{f}({\xi }^{\prime \prime }-\eta )\hat{u}(\eta )d\eta }}.\end{array}$$对于 $I$, 我们用引理的条件, 对任意的正整数 $N⩾1$, 存在常数 $C_N({\Gamma }^{\prime })$, 使得对任意的 ${\xi }^{\prime }\in {\Gamma }^{\prime }$, 我们有$$\left|\hat{u}({\xi }^{\prime })\right|⩽\frac{C_N({\Gamma }^{\prime })}{{\left(1+|{\xi }^{\prime }{|}^2\right)}^{\frac{N}{2}}}.$$所以, $$\begin{array}{rl}(1+|{\xi }^{\prime \prime }|{)}^{N}I& ⩽\frac{1}{(2\pi {)}^n}{\int }_{{\Gamma }^{\prime }}(1+|{\xi }^{\prime \prime }-\eta |+|\eta |{)}^N\left|\hat{f}({\xi }^{\prime \prime }-\eta )\right|\left|\hat{u}(\eta )\right|d\eta \\ & ⩽\frac{1}{(2\pi {)}^n}{\int }_{{\Gamma }^{\prime }}(1+|{\xi }^{\prime \prime }-\eta |{)}^N\left|\hat{f}({\xi }^{\prime \prime }-\eta )\right|(1+|\eta |{)}^N\left|\hat{u}(\eta )\right|d\eta \\ & ⩽\frac{1}{(2\pi {)}^n}{\int }_{{\Gamma }^{\prime }}(1+|{\xi }^{\prime \prime }-\eta |{)}^N\left|\hat{f}({\xi }^{\prime \prime }-\eta )\right|C_N({\Gamma }^{\prime })d\eta \\ & =\frac{C_N({\Gamma }^{\prime })}{(2\pi {)}^n}{\int }_{{\Gamma }^{\prime }}(1+|\eta |{)}^N\left|\hat{f}(\eta )\right|d\eta .\end{array}$$由于 $f\in C_0^{\infty }$, 所以上面的积分是有限的, 从而, $$\begin{array}{rl}(1+|{\xi }^{\prime \prime }|{)}^N& ⩽C_N.\end{array}$$在 $II$ 这一项中, $\eta$ 落在 ${\Gamma }^{\prime }$ 之外.

我们注意到, 此时, 存在 $\delta >0$, 使得$$|{\xi }^{\prime \prime }|⩽\frac{1}{\delta }|{\xi }^{\prime \prime }-\eta |.$$这是因为从 ${\xi }^{\prime \prime }$ 到 $\eta$ 的距离不会小于 ${\xi }^{\prime \prime }$ 到 $\partial {\Gamma }^{\prime }$ 的距离, 而后面这个距离与 $|{\xi }^{\prime \prime }|$ 是成正比的 (投影到 $\partial {\Gamma }^{\prime }$ 上) , 这表明$$|{\xi }^{\prime \prime }-\eta |⩾|{\xi }^{\prime \prime }|\delta .$$类似地, 我们还有$$|{\xi }^{\prime \prime }-\eta |⩾|\eta |\delta .$$

据此, 我们有$$\begin{array}{rl}(1+|{\xi }^{\prime \prime }|{)}^{N}II& ⩽\frac{1}{(2\pi {)}^n}{\int }_{{\mathbb{R}}^n-{\Gamma }^{\prime }}(1+|{\xi }^{\prime \prime }|{)}^N|\hat{f}({\xi }^{\prime \prime }-\eta )||\hat{u}(\eta )|d\eta \\ & ⩽C_{\delta }{\int }_{{\mathbb{R}}^n-{\Gamma }^{\prime }}(1+|{\xi }^{\prime \prime }-\eta |{)}^N|\hat{f}({\xi }^{\prime \prime }-\eta )||\hat{u}(\eta )|d\eta \\ & ⩽C_{\delta }^{\prime }{\int }_{{\mathbb{R}}^n-{\Gamma }^{\prime }}(1+|{\xi }^{\prime \prime }-\eta |{)}^{-\frac{s_0}{2}-n}|\hat{u}(\eta )|d\eta .\end{array}$$最后一步是因为$$(1+|{\xi }^{\prime \prime }-\eta |{)}^N|\hat{f}({\xi }^{\prime \prime }-\eta )|⩽C^{\prime \prime }(1+|{\xi }^{\prime \prime }-\eta |{)}^{-\frac{s_0}{2}-n}.$$从而, $$\begin{array}{rl}(1+|{\xi }^{\prime \prime }|{)}^{N}II& ⩽C_{\delta }^{\prime }{\int }_{{\mathbb{R}}^n-{\Gamma }^{\prime }}(1+|\eta |{)}^{-\frac{s_0}{2}}|\hat{u}(\eta )|\times (1+|\eta |{)}^{-n}d\eta \\ & ⩽C_{\delta }^{\prime }{\left({\int }_{{\mathbb{R}}^n-{\Gamma }^{\prime }}(1+|\eta |{)}^{-s_0}|\hat{u}(\eta ){|}^{2}d\eta \right)}^{\frac{1}{2}}\times {\left({\int }_{{\mathbb{R}}^n-{\Gamma }^{\prime }}(1+|\eta |{)}^{-2n}d\eta \right)}^{\frac{1}{2}}\\ & =C_{\delta }^{\prime }\Vert u{\Vert }_{H^{-s_0}}.\end{array}$$综合上面两个不等式, 我们就得到了$$I+II⩽\frac{C_N}{(1+|\xi |{)}^N}.$$命题得到证明.

$\square$

根据这个引理, 我们有如下重要的推论:

推论 82.4. 给定 $\Omega \subset {\mathbb{R}}^n$, $u\in {\mathcal{D}}^{\prime }(\Omega )$. 对任意的 $\psi (x)\in C^{\infty }(\Omega )$, 我们有$$WF(\psi \cdot u)\subset WF(u).$$

证明. 我们只要证明如果 $(x_0,{\xi }_0)\notin WF(u)$, 那么 $(x_0,{\xi }_0)\notin WF(\psi \cdot u)$ 即可. 根据定义, 存在锥型开集 ${\xi }_0\in \Gamma \subset {\mathbb{R}}_{\xi }^n$, $f\in C_0^{\infty }(\Omega )$, $f(x_0)\ne 0$ 并且对任意的正整数 $N⩾1$, 存在常数 $C_N$, 使得对任意的 $\xi \in \Gamma$, 有$$\left|\widehat{fu}(\xi )\right|⩽\frac{C_N}{{\left(1+|\xi |\right)}^N}.$$我们对 $(u,f)=(fu,\psi )$ 用上面的引理: 存在一个锥型开集 ${\Gamma }^{\prime }‘\subset \Gamma$ 包含 ${\xi }_0$ (这里用到了引理中 ${\Gamma }^{\prime \prime }$ 的任意性) 并且 $\mathring{{\Gamma }^{\prime \prime }}\ne \varnothing$, 使得对任意的正整数 $N⩾1$, 存在常数 $C_N^{\prime \prime }$, 使得对任意的 ${\xi }^{\prime \prime }\in {\Gamma }^{\prime \prime }$, 我们有$$\left|\widehat{f(\psi \cdot u)}({\xi }^{\prime \prime })\right|=\left|\widehat{\psi \cdot fu}({\xi }^{\prime \prime })\right|⩽\frac{C_N^{\prime \prime }}{{\left(1+|{\xi }^{\prime \prime }{|}^2\right)}^{\frac{N}{2}}}.$$这表明 $(x_0,{\xi }_0)\notin WF(\psi \cdot u)$

$\square$

作为这个引理的另一个推论, 我们给出波前集的等价定义:

定理 82.5. $\Omega \subset {\mathbb{R}}^n$ 是开集, $u\in {\mathcal{D}}^{\prime }(\Omega )$ 是 $\Omega$ 上的分布. 给定 $(x_0,{\xi }_0)\in {\left(T^{\ast }\Omega \right)}^{\times }$. 那么, 如下的论断是等价的:

1)	$(x_0,{\xi }_0)\notin WF(u)$;
2)	存在包含 $x_0$ 的开集 $U\subset \Omega$, 包含 ${\xi }_0$ 的锥型开集 $\Gamma \subset {\mathbb{R}}_{\xi }^n$, 使得对任意的 $f\in C_0^{\infty }(U)$, 对任意的正整数 $N⩾1$, 存在常数 $C_{N,f}$, 使得对任意的 $\xi \in \Gamma$, 我们有$$\left|\widehat{fu}(\xi )\right|⩽\frac{C_{N,f}}{{\left(1+|\xi |\right)}^N}.$$

证明. 2)$\Rightarrow$1) 是明显的: 我们只要任意选取一个 $f\in C_0^{\infty }(U)$ 并且 $f(x_0)\ne 0$ 即可. 反之, 我们假设 1) 成立来证明 2): 根据定义, $(x_0,{\xi }_0)\notin WF(u)$ 意味着存在锥型开集 ${\xi }_0\in \Gamma \subset {\mathbb{R}}_{\xi }^n$, $F\in C_0^{\infty }(\Omega )$, $F(x_0)\ne 0$ 并且对任意的正整数 $N⩾1$, 存在常数 $C_N$, 使得对任意的 $\xi \in \Gamma$, 有$$\left|\widehat{Fu}(\xi )\right|⩽\frac{C_N}{{\left(1+|\xi |\right)}^N}.$$由于 $F(x_0)\ne 0$, 所以存在开集 $U$, $x_0\in U$ 并且对任意的 $x\in U$, $|F(x)|>\delta >0$. 我们选定这个开集 $U$. 对任意的 $f\in C_0^{\infty }(U)$, 我们考虑: $$fu=\frac{f}{F}Fu.$$我们对 $(u,f)=\left(Fu,\frac{f}{F}\right)$ 来运用引理: 存在一个锥型开集 ${\Gamma }^{\prime }‘\subset \Gamma$ 包含 ${\xi }_0$ (这里用到了引理中 ${\Gamma }^{\prime \prime }$ 的任意性) 并且 $\mathring{{\Gamma }^{\prime \prime }}\ne \varnothing$, 使得对任意的正整数 $N⩾1$, 存在常数 $C_N^{\prime \prime }$, 使得对任意的 ${\xi }^{\prime \prime }\in {\Gamma }^{\prime \prime }$, 我们有$$\left|\widehat{fu}({\xi }^{\prime \prime })\right|=\left|\widehat{\frac{f}{F}Fu}({\xi }^{\prime \prime })\right|⩽\frac{C_N^{\prime \prime }}{{\left(1+|{\xi }^{\prime \prime }|\right)}^N}.$$此时, 在 2) 中我们选取的锥型开集是 ${\Gamma }^{\prime \prime }$. 命题得证.

$\square$

推论 82.6 (从微局部到局部: 光滑性). 给定 $\Omega \subset {\mathbb{R}}^n$, $u\in {\mathcal{D}}^{\prime }(\Omega )$. 假设 $x_0\in \Omega$ 使得对任意的 $\xi \in {\mathbb{R}}_{\xi }^n$, $(x_0,\xi )\notin WF(u)$ (即 $u$ 在 $(x_0,\xi )$ 处是在微局部意义下光滑的) . 那么, 存在 $x_0$ 在 $\Omega$ 中的开邻域 $U$, 使得 $u{|}_U$ 是光滑的.

证明. 对任意的 $\xi \in {\mathbf{S}}^{n-1}$ (单位长的向量) , $(x_0,\xi )\notin WF(u)$, 从而, 存在锥型开集 $\Gamma \subset {\mathbb{R}}_{\xi }^n$ 和开集 $U$, 其中 $x_0\in U$, $\xi \in \Gamma$, 对任意的 $f\in C_0^{\infty }(U)$, 对任意的正整数 $N⩾1$, 存在常数 $C_{N,f}$, 使得对任意的 $\xi \in \Gamma$, 有$$\left|\widehat{fu}(\xi )\right|⩽\frac{C_{N,f}}{{\left(1+|\xi |\right)}^N}.$$当 $\xi$ 取遍整个 ${\mathbf{S}}^{n-1}$ 时, 它们所对应的上述的 $\Gamma$ 是 ${\mathbf{S}}^{n-1}$ 的一个开覆盖, 所以, 我们可以选出有限个 ${\xi }_1,\cdots ,{\xi }_m\in {\mathbf{S}}^{n-1}$, 使得对每个 $j=1,\cdots ,m$, 存在锥型开集 ${\Gamma }_j\subset {\mathbb{R}}_{\xi }^n$ 和开集 $U_j$, 其中 $x_0\in U$, ${\xi }_j\in \Gamma$, 对任意的 $f\in C_0^{\infty }(U_j)$, 对任意的正整数 $N⩾1$, 存在常数 $C_{j,N,f}$, 使得对任意的 $\xi \in \Gamma$, 有$$\left|\widehat{fu}(\xi )\right|⩽\frac{C_{j,N,f}}{{\left(1+|\xi |\right)}^N}$$并且$$\bigcup _{j=1}^m{\Gamma }_j\supset {\mathbf{S}}^{n-1}\Rightarrow \bigcup _{j=1}^m{\Gamma }_j\supset {\mathbb{R}}_{\xi }^n-\{0\}.$$此时, 我们令 $U=\bigcap _{j⩽m}{U}_j$, 这也是包含 $x_0$ 的开集. 我们任意选取 $f\in C_0^{\infty }(U)\subset C_0^{\infty }(U_j)$, 其中 $f(x_0)\ne 0$. 那么, 对任意的 $\xi \in {\mathbb{R}}^n$, 存在 $j$, 使得 $\xi \in {\Gamma }_j$, 此时, 如果令 $C_N=\underset{j⩽m}{\max }{C}_{j,N,f}$, 那么, 对任意的 $N⩾1$, 我们就有$$\left|\widehat{fu}(\xi )\right|⩽\frac{C_{j,N,f}}{{\left(1+|\xi |\right)}^N}⩽\frac{C_N}{{\left(1+|\xi |\right)}^N}.$$这表明 $fu$ 是光滑函数 (因为它的 Fourier 变换是衰减得比任意的多项式都要快) .

$\square$

我们给出这个推论的一个应用. 我们先回忆微分算子的定义: 给定区域 $\Omega$ 上的一个 $m$-次微分算子 (变系数) , 即$$P=\sum _{|\alpha |⩽m}{p}_{\alpha }(x){\partial }^{\alpha },$$其中, 对每个 $\alpha$, $p_{\alpha }\in C^{\infty }(\Omega )$ 并且至少有一个 $\alpha$ 使得 $|\alpha |=m$ 并且 $p_{\alpha }\ne 0$ (不恒为 $0$) . 我们定义 $P$ 的主象征为$$p_m(x,\xi )=\sum _{|\alpha |=m}{p}_{\alpha }(x)(-i\xi {)}^{\alpha }.$$那么, $p_m(x,\xi )$ 是 $T^{\ast }\Omega =\Omega \times {\mathbb{R}}_{\xi }^n$ 上的光滑函数. 我们把 $p_m$ 的零点集记作$$Z(p_m)=\{(x,\xi )\in T^{\ast }\Omega |p_m(x,\xi )=0\}.$$我们先不加证明的接受如下的定理 (下节课给出完整证明) :

定理 82.7 (微局部椭圆正则性). 给定区域 $\Omega$ 上的一个 $m$-次微分算子$$P=\sum _{|\alpha |⩽m}{p}_{\alpha }(x){\partial }^{\alpha }$$假设 $u\in {\mathcal{D}}^{\prime }(\Omega )$ 满足微分方程$$Pu\stackrel{{\mathcal{D}}^{\prime }}{=}f,$$其中 $f\in {\mathcal{D}}^{\prime }(\Omega )$. 那么, 我们有$$WF(u)\subset Z(p_m)\cup WF(f).$$

我们现在证明 $-△$ 算子的正则性: 假设分布 $u\in {\mathcal{D}}^{\prime }(\Omega )$, 满足 $-△u\in C^{\infty }(\Omega )$, 我们现在来证明 $u\in C^{\infty }(\Omega )$. 实际上, $$p_2(-△)=|\xi {|}^2\Rightarrow Z(p_2)=\{0\}.$$由于 $-△u$ 光滑, 所以 $WF(-△u)=\varnothing$. 利用上述微局部正则性定理, 我们就有$$WF(u)\subset \{0\}\cup \varnothing =\{0\}.$$然而, $WF(u)\subset (T^{\ast }\Omega {)}^{\times }$, 所以, $WF(u)=\varnothing$. 我们刚刚证明的推论表明 $u$ 是光滑的.