2. 基本群胚

道路连通分支 ${\pi }_0$

定义 2.1. 令 $X\in \mathsf{T}\mathsf{o}\mathsf{p}$.

•	映射 $\gamma :I\to X$ 称为从 $\gamma (0)$ 到 $\gamma (1)$ 的一条道路.
•	记号 ${\gamma }^{-1}$ 表示从 $\gamma (1)$ 到 $\gamma (0)$ 的一条道路, 由 ${\gamma }^{-1}(t)=\gamma (1-t)$ 定义.
•	记号 $i_{x_0}:I\to X$ 表示 $x_0\in X$ 处的常值道路.

图 1. 拓扑空间 $X$ 中的一条道路 $\gamma$ 和其逆 ${\gamma }^{-1}$

我们来定义 $X$ 上的一个等价关系: $$x_0\sim x_1⟺\text{存在从x0 到 x1的一条道路}.$$记对应的商空间为: $${\pi }_0(X)=X/\sim$$这就是 $X$ 的道路连通分支所构成的集合.

定理 2.2. ${\pi }_0$ 定义了一个从 $h\mathsf{T}\mathsf{o}\mathsf{p}$ 到 $\mathsf{S}\mathsf{e}\mathsf{t}$ 的协变函子.

证明. 留作练习.

$\square$

推论 2.3. 若 $X,Y$ 同伦等价, 则 ${\pi }_0(X)={\pi }_0(Y)$.

证明. 对函子 ${\pi }_0:h\mathsf{T}\mathsf{o}\mathsf{p}\to \mathsf{S}\mathsf{e}\mathsf{t}$ 应用命题 1.19.

$\square$

道路范畴/基本群胚

定义 2.4. 令 $\gamma :I\to X$ 是一条道路. 我们定义 $\gamma$ 的道路类为$$[\gamma ]=\{\tilde{\gamma }:I\to X|\gamma \simeq \tilde{\gamma }\mathrm{rel}\partial I=\{0,1\}\}.$$

图 2. 在一个道路类中, $F:\gamma \simeq \tilde{\gamma }\mathrm{rel}\partial I$

$[\gamma ]$ 是所有在固定端点时可连续形变到 $\gamma$ 的道路构成的等价类.

定义 2.5. 令 ${\gamma }_1,{\gamma }_2:I\to X$ 使 ${\gamma }_1(1)={\gamma }_2(0)$. 我们按

$${\gamma }_2\star {\gamma }_1(t)=\{\begin{array}{ll}{\gamma }_1(2t)& 0\le t\le 1/2\\ {\gamma }_2(2t-1)& 1/2\le t\le 1,\end{array}$$定义一条合成道路$${\gamma }_2\star {\gamma }_1:I\to X$$

图 3. 道路的合成

命题 2.6. 设 $f_1,f_2,g_1,g_2$ 均是道路, 满足 $f_i(1)=g_i(0)$, $[f_1]=[f_2]$, $[g_1]=[g_2]$. 则$$[g_1\star f_1]=[g_2\star f_2].$$

证明. 下图描述了证明, 其中 $F:f_1\simeq f_2$ 而 $G:g_1\simeq g_2$.

$\square$

我们于是知道 $\star$ 对道路类是良定的:$$\begin{array}{c}[g\star f]:=[g]\star [f].\end{array}$$

命题 2.7 (结合律). 令 $f,g,h:I\to X$ 满足 $f(1)=g(0)$ 和 $g(1)=h(0)$. 这时$$\begin{array}{c}([h]\star [g])\star [f]=[h]\star ([g]\star [f]).\end{array}$$

证明. 下图描述了证明:

$\square$

命题 2.8 (单位元). 令 $\gamma :I\to X$ 的端点分别为 $\gamma (0)=x_0$ 和 $\gamma (1)=x_1$. 则$$[\gamma ]\star [i_{x_0}]=[\gamma ]=[i_{x_1}]\star [\gamma ].$$

证明. 我们只证明第一个等式, 它由下图推出: $\square$

定义 2.9. 令 $X\in \mathsf{T}\mathsf{o}\mathsf{p}$. 我们定义一个范畴 ${\Pi }_1(X)$ 如下:

•	$\mathrm{Obj}({\Pi }_1(X))=X$.
•	${\mathrm{Hom}}_{{\Pi }_1(X)}(x_0,x_1)=\text{从 x0 到 x1 的道路类}$.
•	$1_{x_0}=[i_{x_0}]$.

前面的命题推出 ${\Pi }_1(X)$ 是良定义的范畴. ${\Pi }_1(X)$ 称为 $X$ 的道路范畴或基本群胚.

群胚

定义 2.10. 所有态射可逆的小范畴称为群胚. 所有的群胚构成一个范畴 $\mathsf{G}\mathsf{r}\mathsf{p}\mathsf{d}$.

例子 2.11. 一个群 $G$ 可视为一个群胚 $\underline{G}$, 其中

•	$\mathrm{Obj}(\underline{G})=\{\star \}$ 只有一个对象.
•	${\mathrm{Hom}}_{\underline{G}}(\star ,\star )=G$, 复合由乘法给出.

于是我们得到一个全忠实函子 $\mathsf{G}\mathsf{r}\mathsf{p}\to \mathsf{G}\mathsf{r}\mathsf{p}\mathsf{d}$.

回忆 ${\gamma }^{-1}$ 是 $\gamma$ 的逆.

定理 2.12. 设 $\gamma :I\to X$ 有端点 $\gamma (0)=x_0$ 和 $\gamma (1)=x_1$. 则$$[\gamma ]\star [{\gamma }^{-1}]=[1_{x_1}],\text{and}[{\gamma }^{-1}]\star [\gamma ]=[1_{x_0}].$$换句话说, ${\Pi }_1(X)$ 中所有态射均是同构, 因此 ${\Pi }_1(X)$ 是群胚.

证明. 令 ${\gamma }_u:I\to X$ 使得 ${\gamma }_u(t)=\gamma (tu)$, 其中 $u\in I$ 任意. 下面的图给出同伦 ${\gamma }^{-1}\star \gamma \simeq 1_{x_0}$ 的构造:

$\square$

习题 2.13. 用下面的图, 为定理  2.12 构造一个不同的同伦 ${\gamma }^{-1}\star \gamma \simeq 1_{x_0}$ .

令 $\mathcal{C}$ 是群胚, 定义如下集合$${\Pi }_0(\mathcal{C})=\mathrm{Obj}(\mathcal{C})/\sim ,$$其中 $A\sim B$ 当且仅当在 $\mathcal{C}$ 中 $\exists f:A\to B$. 我们可以将 ${\Pi }_0(\mathcal{C})$ 视为一个 (离散的) 范畴, 其对象是只带有恒同态射的元素. 这样 $\mathcal{C}\to {\Pi }_0(\mathcal{C})$ 定义了一个从 $\mathsf{G}\mathsf{r}\mathsf{p}\mathsf{d}$ 到 $\mathsf{S}\mathsf{e}\mathsf{t}$ 的函子 (这类似于道路连通分支). 如果 ${\Pi }_0(\mathcal{C})$ 只有一个点, 我们就说 $\mathcal{C}$ 是道路连通的.

命题 2.14. $X$ 道路连通当且仅当 ${\Pi }_1(X)$ 道路连通.

证明. 留作练习.

$\square$

定义 2.15. 令 $\mathcal{C}$ 是群胚. 我们将一个对象 $A\in \mathrm{Obj}(\mathcal{C})$ 的自同构群定义为$${\mathrm{Aut}}_{\mathcal{C}}(A):={\mathrm{Hom}}_{\mathcal{C}}(A,A).$$注意它确实构成群.

任意的 $f:A\to B$ 诱导群同构$$\begin{array}{rl}{\mathrm{Ad}}_f:{\mathrm{Aut}}_{\mathcal{C}}(A)& \to {\mathrm{Aut}}_{\mathcal{C}}(B)\\ g& \to f\circ g\circ f^{-1}.\end{array}$$用图表表示, $${\mathrm{Ad}}_f\text{ 将 }A\text{ 映到 }ABggf{f}^{-1}$$

这便自然定义了函子$$\begin{array}{rl}\mathcal{C}& \to \mathsf{G}\mathsf{r}\mathsf{p}\text{定义为}A\mapsto {\mathrm{Aut}}_{\mathcal{C}}(A),f\mapsto {\mathrm{Ad}}_f.\end{array}$$特别地, 把它应用到拓扑空间上, 就得到了函子$$\begin{array}{c}{\Pi }_1(X)\to \mathsf{G}\mathsf{r}\mathsf{p}.\end{array}$$

定义 2.16. 令 $x_0\in X$, 群$${\pi }_1(X,x_0):={\mathrm{Aut}}_{{\Pi }_1(X)}(x_0)$$称为带基点的空间 $(X,x_0)$ 的基本群.

定理 2.17. 令 $X$ 道路连通. 则对于任意 $x_0,x_1\in X$, 我们都有群同构$${\pi }_1(X,x_0)\cong {\pi }_1(X,x_1).$$

证明. 考虑上述的函子 ${\Pi }_1(X)\to \mathsf{G}\mathsf{r}\mathsf{p}$. 因为 $X$ 道路连通, ${\Pi }_1(X)$ 是群胚, 任两点 $x_0$ 和 $x_1$ 在 ${\Pi }_1(X)$ 中同构. 由命题 1.19, ${\pi }_1(X,x_0)\cong {\pi }_1(X,x_1)$.

$\square$

鉴于定理 2.17, 在道路连通的情况下, 我们有时就简单地将 $X$ 的基本群记为 ${\pi }_1(X)$ 而不点明基点.

令 $f:X\to Y$ 是连续映射. 则它定义了函子$$\begin{array}{rl}{\Pi }_1(f):{\Pi }_1(X)& \to {\Pi }_1(Y)\text{定义为}x\mapsto f(x),[\gamma ]\mapsto [f\circ \gamma ].\end{array}$$

命题 2.18. ${\Pi }_1$ 定义了函子$${\Pi }_1:\mathsf{T}\mathsf{o}\mathsf{p}\to \mathsf{G}\mathsf{r}\mathsf{p}\mathsf{d},$$其将 $X$ 映为 ${\Pi }_1(X)$.

证明. 留作练习.

$\square$

命题 2.19. 令 $f,g:X\to Y$ 是映射, 通过 $F:X\times I\to Y$ 同伦. 我们定义道路类$${\tau }_x=[F{|}_{x\times I}]\in {\mathrm{Hom}}_{{\Pi }_1(Y)}(f(x),g(x)),x\in X$$如下图所示:则 ${\tau }_F:=\{{\tau }_x:x\in X\}$ 定义了自然变换$${\tau }_F:{\Pi }_1(f)⟹{\Pi }_1(g).$$

证明. 令 $r:I\to X$ , $r(0)=x_0$ , $r(1)=x_1$. 我们要证明在道路类的层次上, 下图交换:合成 $F\circ (r\times I)$ 给出如下的同伦:这导出 $[g\circ r]\star [{\tau }_{x_0}]=[{\tau }_{x_1}]\star [f\circ r]$, 即证.

$\square$

这个命题可以总结为如下的图表.$$\mathsf{T}\mathsf{o}\mathsf{p}\mathsf{G}\mathsf{r}\mathsf{p}\mathsf{d}X{\Pi }_1(X)\underset{F}{\overset{\text{同伦}}{\Rightarrow }}\underset{{\tau }_F}{\overset{\text{自然变换}}{\Rightarrow }}Y{\Pi }_1(Y){\Pi }_{1}fg{\Pi }_1(f){\Pi }_1(g)$$下面的定理是上面命题的形式推论.

定理 2.20. 令 $f:X\to Y$ 是同伦等价. 则$${\Pi }_1(f):{\Pi }_1(X)\to {\Pi }_1(Y)$$是范畴等价. 特别地, 它诱导了群同构$${\pi }_1(X,x_0)\cong {\pi }_1(Y,f(x_0)).$$

证明. 令 $g:Y\to X$ 代表 $f$ 在 $h\mathsf{T}\mathsf{o}\mathsf{p}$ 中的逆. 将 ${\Pi }_1$ 应用到同伦 $f\circ g\simeq 1_Y$ 和 $g\circ f\simeq 1_X$ 上, 我们就找到了从 ${\Pi }_1(f)\circ {\Pi }_1(g)$ 和 ${\Pi }_1(g)\circ {\Pi }_1(f)$ 到恒同函子的自然变换. 因为 ${\Pi }_1(X)$ 和 ${\Pi }_1(Y)$ 是群胚, 这些自然变换一定是自然同构. 于是得到第一个命题. 第二个命题则是 1.26 的推论.

$\square$

命题 2.21. 令 $X,Y\in \mathsf{T}\mathsf{o}\mathsf{p}$. 则我们有范畴的典范同构$${\Pi }_1(X\times Y)\cong {\Pi }_1(X)\times {\Pi }_1(Y).$$特别地, 对任意 $x_0\in X,y_0\in Y$, 我们有群同构$${\pi }_1(X\times Y,x_0\times y_0)\cong {\pi }_1(X,x_0)\times {\pi }_1(Y,y_0).$$

证明. 留作练习.

$\square$

例子 2.22. 对于点 $X=\text{pt}$, ${\pi }_1(\text{pt})=0$ 是平凡的. 不难看出, ${\mathbb{R}}^n$ 和一个点同伦等价. 因此$${\pi }_1({\mathbb{R}}^n)=0,\forall n\ge 0.$$

例子 2.23. 我们将在 3 和 ?? 中证明,$${\pi }_1(S^1)=\mathbb{Z},\text{且}{\pi }_1(S^n)=0,\forall n>1.$$

例子 2.24. 令 $T^n=(S^1{)}^n$ 是 $n$-维环面. 则$${\pi }_1(T^n)={\mathbb{Z}}^n.$$

例子 2.25 (辫群). $n$ 条线的 Artin 辫群 ${\mathrm{Br}}_n$ 可以实现为有 $n$ 个洞的圆盘的映射类群 (对称群). 它具有如下的有限表现: $$\begin{array}{rcl}{\mathrm{Br}}_n=⟨b_1,\dots ,b_{n-1}\mid & b_i{b}_j{b}_i=b_j{b}_i{b}_j& \forall |j-i|=1,\\ & b_j{b}_i=b_i{b}_j& \forall |j-i|>1⟩.\end{array}$$辫群也可以实现为基本群.

令 $X\in \mathsf{T}\mathsf{o}\mathsf{p}$. $X$ 的 $n$ 点 (有序) 构形空间是 $X$ 中 $n$ 个两两不同的点组成的集合: $${\mathrm{Conf}}_n(X):=\{\underline{x}=(x_1,\dots ,x_n)\in X^n\mid x_i\ne x_j,\forall i\ne j\}.$$置换群 $S_n$ 在 ${\mathrm{Conf}}_n(X)$ 上有自然作用如下$$\begin{array}{rl}{S}_n\times {\mathrm{Conf}}_n(X)& ⟶{\mathrm{Conf}}_n(X)\\ (\sigma ,\underline{x})& ⟼\sigma (\underline{x})=(x_{\sigma (1)},x_{\sigma (2)},\dots ,x_{\sigma (n)}).\end{array}$$$X$ 的无序构形空间是这个作用的轨道: $${\mathrm{UConf}}_n(X)={\mathrm{Conf}}_n(X)/S_n.$$

一个经典的结果是$${\mathrm{Br}}_n\cong {\pi }_1({\mathrm{UConf}}_n({\mathbb{R}}^2))\cong {\pi }_1({\mathrm{UConf}}_n(D^2)).$$

更进一步, 这个 (基本) 群中的元素可以这样直观地看成 ${\mathbb{R}}^3$ 中的辫子, 方法如下. 固定 $n$ 个 ${\mathbb{R}}^2$ 中的不同点 $Z_1,\cdots ,Z_n$. 几何辫是指一个 $n$-元组 $\Psi =({\psi }_1,\dots ,{\psi }_n)$, 其中 ${\psi }_i$ 是路径$${\psi }_i:[0,1]\to {\mathbb{R}}^2\times I\subset {\mathbb{R}}^3$$使得

•	${\psi }_i(0)=Z_i\times \{0\}$;
•	${\psi }_i(1)=Z_{\sigma (i)}\times \{1\}$ 其中 $\sigma$ 是某个 $\{1,\dots ,n\}$ 的置换;
•	对任意 $0\le t\le 1$, $\{{\psi }_1(t),\dots ,{\psi }_n(t)\}$ 是 ${\mathbb{R}}^2\times \{t\}$ 中的不同的点.

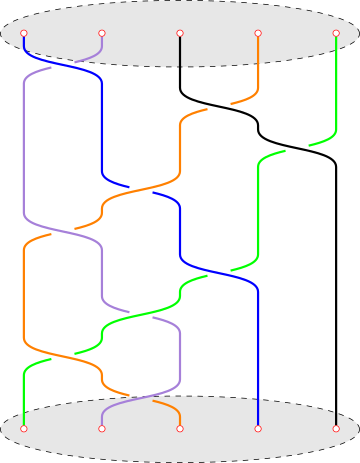
几何辫的乘法用和道路 (在基本群中) 的乘法一样的方式给出. ${\mathbb{R}}^3$ 中所有辫子的同痕类, 连同如上定义的乘法构成辫群. 在图 4 中可以看到辫子$$b_1{b}_3{b}_4{b}_2^{-1}{b}_1{b}_3{b}_2^{-1}{b}_1{b}_2^{-1}.$$

图 4. 经典的辫子

术语翻译

$n$ 点 (有序/无序) 构形空间 • 英文 $n^{\text{th}}$ (ordered/unordered) configuration space