5. Sieving
5.1Mobius Inversion and Inclusion-Exclusion
在这一章中, 我们主要考虑一些会出现 " 减号 " 的组合问题. 准确来说, 我们会考虑组合中十分传统的容斥原理, 然后其组合物种的扩展. 同时, 我们还会考虑矩阵树定理的一些应用和棋盘多项式.
Definition 5.1.1. For poset , for define interval .
Definition 5.1.2. We say poset is locally finite if all intervals are finite.
Remark 5.1.3. In this course we would assume the poset is always locally finite.
Example 5.1.4.
1. | is locally finite. |
2. | is locally finite where is divisibility, e.g. and . |
3. | Consider , where is the set of all finite subsets of with any fixed set. |
4. | Consider where is the set of all partitions, with the “diagram containment” relation. (Example deleted since I don’t want to include graphics) |
5. | Consider , where is a directed acyclic graphs, and means there exists a directed path from to . |
Definition 5.1.5 (Mobius Function). Let be a poset. Define recursively as follows:
Example 5.1.6. Classical Mobius function given bySince the RHS depends only on , we write .
Theorem 5.1.7. Let and be two posets, then we can define poset by iff . Then we have
Theorem 5.1.8 (Mobius Inversion, Version I). Let be a ring, with a poset. The following are equivalent:
1. | for all . |
2. | for all . |
where we assume the sums are finite, or is a valuation ring and sums are convergent.
Corollary 5.1.9 (Mobius Inversion, Version II). With the same setting as above, the following are equivalent:
1. | for all . |
2. | for all . |
where we assume the sums are finite or is valuation ring with sum convergent.
Remark 5.1.10 (Inclusion-Exclusion). Now consider , we want to compute the Mobius inversion on this poset. It is not hard to see
Now we discuss the combinatorial set-up of this. Let be a set of objects, be the set of “good” objects with the set of “flaws” (that exclude an object from being “good”).
For , we can define .
For , we can define , which is the set of objects with flaws , and possibly others. We can also define as . We note and .
Then the basic formulation with finite is that, , with , . Then we have a theorem as follows:
Indeed, by construction, and so by Mobius inversion on the result follows.
In particular, we see .
Example 5.1.11 (Derangements). Let be permutations of , be the set of derangements. Then the flaws are . In other word, we can think the set . Then . Thenand hence Thus, we get
Example 5.1.12 (Rook Polynomials).
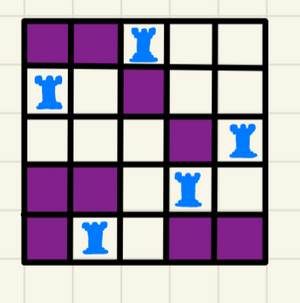
Consider as the squares of a by chess board, then a permutation is a placement of non-attacking rooks on the chess board.
Now we want to look at rook placements with some blocks disallowed, for example,
where we want non-attacking rook placements with none of the rooks placed on the purple blocks.
Formally, let be the set of disallowed squares, let be the set of placements of non-attacking rooks avoiding . Then we want to compute .
For this purpose, we define the rook polynomial where is the number of ways to place non-attacking rooks within squares of . Then we have a theorem
To prove this, we apply inclusion-exclusion to with the set of “flaws”. For , let . ThenThen we see
Example 5.1.13 (Menage Problem). The set-up is:
1. | We have male-female couples. |
2. | Seat them around a round table. |
3. | No person is next to someone of the same sex. |
4. | No person is next to their partner. |
Then we want to compute the number of such seatings.
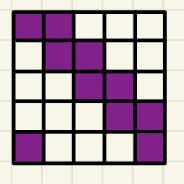
Fix a seating of men in every other seat. Then the number of ways to seat the women is equivalent to count , such that . This is just the following disallowed squares configuration:
Then by elementary counting, we can show and use the theorem about rook polynomial to get the answer.
Remark 5.1.14 (GF Formulation). Now consider the generating function formulation of the inclusion-exclusion principle. Let as before.
We introduce a weight function on this set-up. Let be a ring, be a generalized weight function with and . Then our usual goal is to compute .
Then we consider the objects with “marked flaws”. Let and . We can think of as object with marked flaws, where not all flaws need to be marked. Then is the subset in which all flaws are marked. We note we have bijection .
Then we have the inclusion-exclusion principle, full version, as follows: let be the set of variables. For , we write . Then we defineThen the theorem sayswhere means substitute by for all .
Proof: We see andThen we see
We also have the inclusion exclusion principle, simplified version. In this version, we just set all variables . Then we get and . Then we have and .
In some applications, can be a set of “features” rather “flaws”. In this case, since has bijection to , is a generating function for , where marks the number of features.
Example 5.1.15. Let be the set of -strings where is not a substring. Then is the set of all -strings. Let be the set of -strings with as a substring, may be marked. For example, we have the following are distinct elements of : where indicates that part has been marked. Then we see where we use to mean is marked. Then where is mark the length, and marks the number of marked . Finally, by inclusion exclusion, we get
Remark 5.1.16 (Matrix Tree Theorem). The inclusion-exclusion set-up:
1. | is a finite set. |
2. | is the set of all endofunctions from . |
3. | is the set of endofunctions from to , where every recurrent element is fixed. In other word, if then . Equivalently, no cycles of length greater than or equal . |
4. | Then contains , where is endofunction and a set of “marked flaws”, i.e. cycles of length . For example, |
5. | Let be the complete graph with vertex set . Then we consider variable for all , and for . Then for , we define |
With the above set-up, we can state the matrix tree theorem as follows.
Theorem 5.1.17. Let be the matrix with rows and columns indexed by , then we defineThen .
Proof. By inclusion-exclusion, we see . We need to show .
Expanding . First level expansion we getThen each of the product we can expandThe terms in the expansion of is the same as we make a choice of permutations plus a choice of terms from each .
5.2Marked and Virtual Species
Remark 5.2.1 (Weighted Species Techniques). The set-up:
1. | Let be a species, which is structures that can have flaws. |
2. | Let be the subspecies of which are good. |
3. | Let be the weighted species of -structures with marked flaws with weight as the number of marks. |
Then by inclusion exclusion we get .
Example 5.2.2. We will re-do the example of derangements: let be permutations with flaws being fixed points. Then is going to be the subspecies of derangements. Then let be the permutation with marked fixed points. For example, we havewhere means they are marked. Then we have where is the set of marked fixed points and is a permutation of the rest. Then the weight on is just the order, to match our weight on . Thus the MGF of is . On the other hand, we would have .
Remark 5.2.3 (-Species Technique). Let and as before. We assume: for , we have . Then we define be the -species of “split” -structure with marked flaws. The unmarked labels are the st sort, and the marked labels are the second sort. Then .
Example 5.2.4. Let us do the derangement example again. An example of iswhere the input set is . Then we have and hence the EGF is and hence we are done.
Example 5.2.5 (Feature, Not Bugs!). In this example we consider an example where we have features, instead of flaws. Let be a weighted species, weight function equal the number of widgets. Let be the weighted species of -structures with marked widgets with weight function equal the number of marks. Then .
The example we are going to consider is permutations and descents. If , and , then we say is a descent of . The question is, how many permutations of with descents?
Here we consider the linear species of permutations . In other word, the input should be an ordered list instead of a set and we should produce the set of permutation of the given list. Let the weight function on is the number of descents. Let be the linear species of permutations with marked descents with weight function equal the number of marks.
Then let be the linear species of decreasing sequences of length with weight function being the order minus . For example, we have and has weight . Then the MGF of should beThen we see we get decomposition and it is a weighted equivalence. Thus we getFinally, we get
Definition 5.2.6. Let be a ring with not a zero-divisor. Let be two sets with generalized weight functions . Then suppose is a bijection, then we say is sign-reversing bijection (SRB) if for all .
Remark 5.2.7. If a SRB exists between and then .
Now we talk about the common scenarios of SRB.
Proposition 5.2.8. Let , suppose there exists SRB then .
Remark 5.2.9. If , then is called a sign-reversing involution (SRI).
Example 5.2.10 (Euler’s Pentagonal Number Theorem). Let be the set of strict partitions, i.e. with . Then we have weight beThen let be the pentagonal partitions, which is equalThen there exists a SRI . Thus we havewhere is the pentagonal numbers.
Remark 5.2.11 (What is Virtual Species). We consider the analogy:
1. | The species are like natural numbers (we have operations like ). |
2. | Then generalized weighted species are like , which is functions from to (we also have operations like ). |
3. | Then, virtual species are like integers, as we note subtraction for natural numbers are only partially defined, e.g. is not defined in . |
Thus, to define virtual species, we recall the construction of :
1. | We start with the set . In other word, this is the set of functions from set map to . We can write these functions as pairs, i.e. . |
2. | Then we can add interpretations of those functions to think them as integers. The idea is that function represents integer . However, does not make sense yet. To achieve this, we define an equivalence relation on , which is if and only if . |
3. | Then we have an embedding . In other word, if we have natural number , then we can identify as the function . For , we have if and only if . |
4. | Negation of integers. For integer , we can define as the function . |
5. | Addition of integers. We can define as addition as functions. |
6. | We can also subtract integers. In other word, we just define as . |
7. | Thus we have defined the additive group . |
8. | We still have one operation left, which is multiplication. This is not just the product of functions, the reason is that integer multiplication must respect the equivalence relation. If and , then we must have . The function multiplication does not have this property. The correct formula isThis is the unique formula satisfying distributive property and rules about negation. |
9. | New definitions of consists with the old definitions when we consider embedded into . |
Definition 5.2.12 (Virtual Species). A virtual species is a generalized weighted species, with generalized weight function . We can also think as a pair of ordinary (unweighted) species, called . The is defined to be and similarly .
Definition 5.2.13.
Suppose be two virtual species, we say are virtually equivalent and write if and only if .
Remark 5.2.14. Every ordinary species can be turned into a virtual species by giving it constant sign function . If are ordinary species, then if and only if .
Definition 5.2.15. Let be a virtual species, we define the negation of a virtual species as with .
Definition 5.2.16. Let be virtual species, then addition is defined as as addition of generalized weighted species. Then subtraction is defined to be .
Remark 5.2.17. Under such definitions, we get . Thus what about other operations? For most, same definitions as generalized weighted species. For others, the GWS definitions does not respect virtual equivalence.
Finally, our new definitions will be consistent with the old definitions.
Remark 5.2.18 (Why Virtual Species?).
1. | We have seen some species with no known decomposition but can still get EGF by inclusion exclusion. |
2. | However, IE is based on numerical equivalence, not natural equivalence. |
3. | Thus to go beyond EGFs, this is not good enough. |
4. | Sometimes, when we do not have decomposition, we can come up some virtual decomposition. |
Definition 5.2.19. Let be a virtual species, then the EGF of is just wherewhere .
Remark 5.2.20. A virtual species operation is good, if it respects the virtual equivalence relation. For example, if is a virtual species operation, with and then we must have .
Definition 5.2.21. The virtual species operations for filters, products (all three), sequences and derivatives and rootings are just the generalized weighted species operation.
Remark 5.2.22. In other word, the GWS definitions for the above operations respect virtual equivalence. We note:
1. | Perform operations on bases species (base ). |
2. | Add sign functions according the rules: sign of composite objects is the product of the signs of its components. |
In this case, the EGF is just given by the main theorem.
We note the concept of “base species” does not respect virtual equivalence, i.e. does not imply the base of is equivalent to the base of . But nonetheless, these operations do respect virtual equivalence.
Example 5.2.23 (Products). We have . However, this is justThen we look at the signs and we get
Definition 5.2.24. If then we say is a multiplicative inverse of .
Theorem 5.2.25.
1. | has a multiplicative inverse if and only if . |
2. | Assume has multiplication inverse , then it is unique up to virtual equivalence. |
3. | If then . |
4. | The EGF of is . |
Example 5.2.26. We have where we see the left part is just ordered set partitions with even number of parts and the right sum is ordered set partitions with odd number of parts.
Remark 5.2.27. We finally talk about virtual multisort species. Everything so far extends to multisort species. Moreover, the diagonal operation on generalized weighted -species also respect virtual equivalence.
Remark 5.2.28 (Compositions). We will not give a definition of virtual species composition. Instead, we will give a set of rules so that we can compute virtual species compositions.
Let be ordinary connected -species or -species. Let be virtual -species and be virtual -species.
Then we have:
1. | . |
2. | . |
3. | . |
4. | . |
5. | . |
6. | . |
7. | . |
In each of the case, the rule is a slight generalizations of an identity for ordinary species. For example, for , we can define . Then . Now let be virtual and , then we get in the above rule.
Example 5.2.29. If is connected virtual species, then .
Proof: We see . Then by rule , we get this is the same asNow apply rule , we get this isNow use rule , we getHowever, we note the multiplicative identity for the operation superposition is , and hence we getThus by use rule and a few times, we would get
Theorem 5.2.30.
1. | Rule to can be used to compute for any virtual species with connected |
2. | Virtual species composition respects . |
3. | EGF of is . |
Remark 5.2.31. Recall -species inclusion exclusion technique:
1. | is a species with structures have flaws . |
2. | is the species of good -structures. |
3. | is the -species of split -structures with marked flaws. |
In this set-up, we have the following theorem.
Theorem 5.2.32. .
5.3Counting With Automorphism
Definition 5.3.1. Let be a finite group, a finite set of “points” with a -action. Then we define the orbit of is given byWe write the set of all orbits as . We define the stabilizer of is given byWe define the fixed points of by
Remark 5.3.2. We recall the orbit-stabilizer theorem, which states . We also recall the orbit counting lemma, which statesNow we prove this. We see
Example 5.3.3. How many ways can we colour -gon up to rotation? Well, let be the set of colours, say , and let our group be , which we can think as sides of -gon.
We want to count , which we can think as functions from to , which correspond to a way of colour the -gon. The group action will be, for function and , we define -action
Then our goal is to count the orbits. Hence we need to look at fixed points. For , we see Thus we see and hencewhere is the Totient function.
Example 5.3.4. Let . How many -orbits? Again, this -action would given by with . To use generating function, we let , then we let weight function be with . Note for and hence
Now we want to generalize this to count fixed points. For , we see is in bijection with where . Thus, we see and henceNow by orbit counting lemma, we get
Remark 5.3.5 (Type Generating Function). Let be a species, the symmetric group of . Then we have a -action of sets of structures on . For and , we havewhere is transportation of -structures along . In particular, the isomorphism type of order are exactly the -orbits on .
In this case, we can define type generating functions. For an isomorphism type , write . Then the type generating function for is the OGF for with respect to . In other word,
Example 5.3.6.
1. | Consider the species . We see we have isomorphism type of each order, thus |
2. | Consider the rooted linear order . We see has isomorphism type of each order , thus the rooted version has non-isomorphic ways to root. Thus |
3. | Consider , the species of permutations. The cycle type of a permutation is the partition such that are the lengths of the cycles of . Then we see two permutations are isomorphic iff they have the same cycle type. In other word |
Proposition 5.3.7. Let be two species, then
1. | TGF of is . |
2. | TGF of is . |
Remark 5.3.8. However, this is all we get. For other operations, TGF of output species cannot be determined from TGF of input. For example, and have the same TGF, but and have different TGF.
Definition 5.3.9. Let be a finite group, a species. Then a natural -action on is a rule that assigns to each group element a natural equivalence such that for every finite set , we get a -group action on given by
Definition 5.3.10. Let acts naturally on . We define the species of orbits to be
Example 5.3.11. We see acts naturally on . For and , we defineThis is a natural -action and
Remark 5.3.12 (Speciesification). Let be a subgroup of , be a finite set with -action. The natural action of on will beThen the speciesification will be defined as
Proposition 5.3.13. Let be a subgroup of , a finite set with -action. Then there is a bijection
Example 5.3.14. Say be the colourings of sides of -gon with -action. Then .
Remark 5.3.15 (Cycle Index Functions). Let be a species, we are going to construct the cycle index function , which is a algebraic transformation.
First, for a species we can construct the species of automorphisms as follows. For , is an automorphism of iff . Then is a subspecies of , given by
Then the TGF of species of automorphisms is given byusingThus we get
However, this may not be helpful if is hard to compute. Thus, we consider the power evaluation maps for . In particular, is given by . Then for a partition , we define the algebraic transformationasIn particular, if then .
For permutation , with the cycle type . Then we write . Now we can define the cycle index function (which is an algebraic transformation) as followsWe can think this as generalized EGF for with .
Proposition 5.3.16.
Definition 5.3.17. We define be the closed subring of generated over in . In other word,where is the set of integer partitions. We also define .
Theorem 5.3.18. The set of is -linearly independent.
Remark 5.3.19 (Implications). Some implications of the above theorem includes:
1. | For , we can define |
2. | We can also define partial derivative |
Proposition 5.3.20. Let and . Then
1. | where . |
2. | where . |
3. | (composition) is left homomorphic, i.e. if , then |
Corollary 5.3.21. is closed under composition.
Example 5.3.22. We have
Remark 5.3.23 (Dual Basis). Let , define using one of the three definitions:
1. | If , with cycle type , then where means the centralizer of . |
2. | If , then |
3. | If equal the number of parts of size in , then |
We often prefer to write elements of in the formand we will write . The analogy is as to and as to .
Remark 5.3.24 (Cycle Index Functions In Dual Basis). Say is a species, andThen for any permutation with cycle type , we have
Remark 5.3.25 (Symmetric Functions). Let , we associate symmetric function defined as follows:Since each expression is symmetric in variables , the overall expression is symmetric.
On the other hand, we have equivalent description of , which is the unique FPS with the propertyfor all tuples .
Then, use symmetric function theory, we can express in terms of provided
Example 5.3.26. Let be the species of linear orders. Since linear orders have no non-trivial automorphisms, we seeHence we get
Next, consider be the species of sets. Then every permutation is going to be an automorphism. Thus where the generalized weight function is . We see and the weight on should be where is the order of and the weight on is the trivial one. Then the generalized EGF for is and hence .
Next, we look at . We see . WriteThen for any , , we have . Therefore,
Finally, let’s look at . For , let be the cycle subgroup generated by . Then . If , then has permutations of cycle type for all . Thus
Theorem 5.3.27 (Main Theorem). Let be two species, with and . Then:
1. | has cycle index function . |
2. | has cycle index function . |
3. | has CIF . |
4. | has CIF . |
5. | has CIF provided its defined. |
6. | has CIF . |
7. | has CIF . |
8. | has CIF if is connected. |
Corollary 5.3.28. The TGF of is .
Example 5.3.29. We revisit the colouring of -gon. Previously, we see where is the set of colours with -action. Then . Then . The cycle index function for evaluated at isWe can just expand this and get
Example 5.3.30 (Rooted Trees). Consider rooted trees. We see . ThusWrite thenCompare coefficients of on both sides, we getwhich is a recurrence relation which defines in terms of .
Example 5.3.31 (Endofunctions). We see , then . Then
Example 5.3.32 (Unrooted Trees). There is no general way to get from , but for trees there is a trick.
In particular, we haveTo see this, we note there are two types of unlabelled trees:
1. | Trees for which every automorphism has a fixed vertex. |
2. | Trees which have a fixed point free automorphism. |
For , let be the number of ways to root at vertex up to isomorphism. We also let be the number of ways to root at edge up to isomorphism.
For type , we have and for type we get . Next, note the number of unrooted trees is equal the number of vertex rooted trees minus number of edge rooted trees plus number of type trees.