16. 空间填充曲线, L’Hôpital 法则, Taylor 展开

空间填充曲线

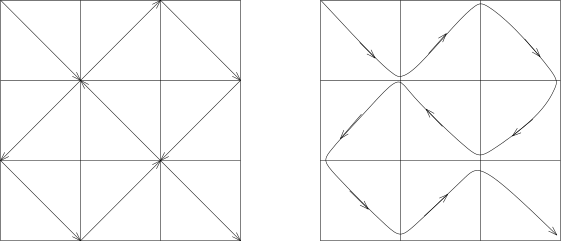
利用一致收敛的想法, 我们可以构造一个很有趣的 (很重要的反例) 例子: 令 $I=\{x\in \mathbb{R}|0⩽x⩽1\}$, $C=\{(x,y)\in {\mathbb{R}}^2|0⩽x⩽1,0⩽y⩽1\}$, 我们按照如下的图像来定义映射$$f_1:I\to C,$$

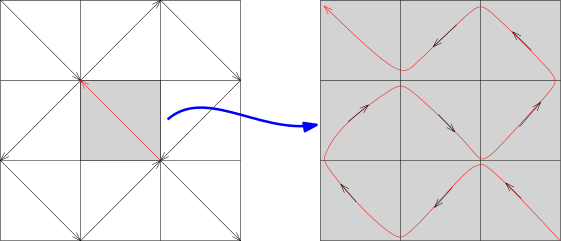
我们对每一个小的正方形根据箭头的方向构造同样的映射, 以中间这个灰色的为例子, 我们要把刚才第一个图中的格子转 $180^{\circ }$, 这样得到下面的图像:

其中, 我们把 $I$ 这个线段映射为图中所画的 9 段折线, 折线走的方向如第二个图所示. 这样子, 我们把 $C$ 分成了 $81$ 个格子, 并且构造出一条 $81$ 段的折线:

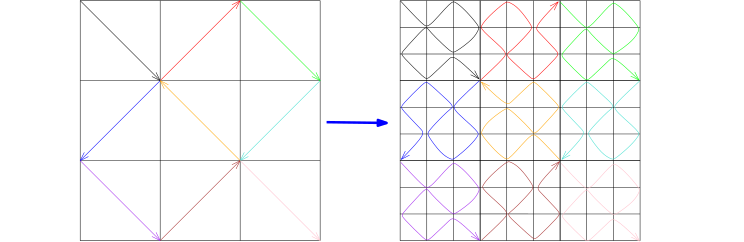
上面这个图对应着映射: $$f_2:I\to C,$$重复上面的操作, 我们就得到了一串连续映射: $$f_n:I\to C,$$其中 $n⩾1$, 并且这是一个 $9^n$ 段的折线. 按照这些映射的构造方式, 我们知道, 对任意的 $N⩾1$, 对任意的 $n,m⩾N$, $f_n$ 和 $f_m$ 都是对 $f_N$ 的每个边长为 $3^{-N}$ 的方块里面进行修改, 特别地, 对任意的 $x\in I$, 我们就知道 $f_n(x)$ 和 $f_m(x)$ 都落在同一个边长为 $3^{-N}$ 的方块里, 所以$$|f_n(x)-f_m(x)|⩽\sqrt{2}\cdot 3^{-N},$$即$$\Vert f_n-f_m{\Vert }_{L^{\infty }}⩽\sqrt{2}\cdot 3^{-N},$$这表明 $\{f_n{\}}_{n⩾1}$ 是 $(C(I;{\mathbb{R}}^2),\Vert \cdot {\Vert }_{\infty })$ 中的 Cauchy 列, 从而存在连续映射$$f_{\infty }:I\to C,$$使得 $f_n\stackrel{C(I;{\mathbb{R}}^2)}{⟶}{f}_{\infty }$. 根据 $f_n$ 的构造, 对任意的 $p\in C$, $p$ 一定落在 $f_n$ 所对应的 $9^n$ 个小方块中的某一个, 所以有 $x\in I$, 使得 $p$ 和 $f_n(x)$ 的距离不超过 $\sqrt{2}\cdot 3^{-n}$, 据此, 我们知道 $f_{\infty }$ 的像 $f_{\infty }(I)\subset C$ 是稠密的. 由于 $I$ 是紧集, 所以它在连续映射下的像是紧的, 从而是闭的, 再用稠密性, 我们就知道 $f_{\infty }(I)=C$. 最终, 我们得到连续的满射: $$f_{\infty }:I\to C.$$

L’Hôpital 法则

我们回到导数的学习, 上次课证明了 Cauchy 中值定理: 实值函数 $f,g\in C^0([a,b])$ 并且 $f$ 和 $g$ 均在 $(a,b)$ 上可微, 若对任意的 $x\in (a,b)$, $g^{\prime }(x)\ne 0$. 那么, 存在 $x_0\in (a,b)$, 使得$$\frac{f^{\prime }(x_0)}{g^{\prime }(x_0)}=\frac{f(b)-f(a)}{g(b)-g(a)}.$$

Cauchy 中值定理的重要应用是用来证明 L’Hôpital 法则:

命题 16.1 (L’Hôpital 法则). 假设 $f$ 和 $g$ 是区间 $(a,b)$ 上的可微实值函数, 我们假设 $f(x),g(x)=o(1)(x\to a)$, 即$$\underset{x\to a^{+}}{\lim }f(x)=0,\underset{x\to a^{+}}{\lim }g(x)=0.$$我们假设对任意的 $x\in (a,b)$, $g^{\prime }(x)\ne 0$. 如果极限 $\underset{x\to a^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$ 存在 (可以是 $\pm \infty$) , 那么$$\underset{x\to a^{+}}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}.$$

证明. 根据 $f(x),g(x)=f(x),g(x)=o(1)(x\to a)$, 我们知道对任意的 $x\in (a,b)$, $f$ 和 $g$ 在区间 $[a,x]$ 上连续并且在 $(a,x)$ 上可微. 所以, 利用 Cauchy 中值定理, 存在 $\xi (x)\in (a,x)$, 使得$$\frac{f(x)}{g(x)}=\frac{f(x)-f(a)}{g(x)-g(a)}=\frac{f^{\prime }(\xi (x))}{g^{\prime }(\xi (x))}.$$特别地, 当 $x\to a^{+}$ 时, 由于 $a<\xi (x)<x$, 所以 $\xi (x)\to a^{+}$. 对上面的式子取极限, 我们就得到: $$\underset{x\to a^{+}}{\lim }\frac{f(x)}{g(x)}=\frac{f(x)-f(a)}{g(x)-g(a)}=\underset{x\to a^{+}}{\lim }\frac{f^{\prime }(\xi (x))}{g^{\prime }(\xi (x))}=\underset{x\to a^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}.$$命题得证.

$\square$

我们还有一个版本 L’Hôpital 法则:

推论 16.2 (L’Hôpital 法则). 实值函数 $f$ 和 $g$ 在区间 $(a,+\infty )$ 上可微并且$$\underset{x\to +\infty }{\lim }f(x)=0,\underset{x\to +\infty }{\lim }g(x)=0.$$假设对任意的 $x\in (a,+\infty )$, $g^{\prime }(x)\ne 0$. 如果极限 $\underset{x\to +\infty }{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$ 存在 (可以是 $\pm \infty$) , 那么我们有$$\underset{x\to +\infty }{\lim }\frac{f(x)}{g(x)}=\underset{x\to +\infty }{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}.$$

证明. 不妨假设 $a>0$, 考虑坐标变换: $$\phi :(0,\frac{1}{a})\to (a,\infty ),x\mapsto \frac{1}{x}.$$从而, $\tilde{f}=f\circ \phi$ 是 $(0,\frac{1}{a})$ 上的函数, 即 $\tilde{f}(x)=f\left(\frac{1}{x}\right)$; 类似地, 我们定义 $(0,\frac{1}{a})$ 上的函数 $\tilde{g}=g\circ \phi$ 是. 由于 $x\to +\infty$ 等价于 $\phi (x)\to 0^{+}$, 所以$$\underset{x\to 0^{+}}{\lim }\tilde{f}(x)=0,\underset{x\to 0^{+}}{\lim }\tilde{g}(x)=0.$$此时, 我们有$$\underset{x\to 0^{+}}{\lim }\frac{{\tilde{f}}^{\prime }(x)}{{\tilde{g}}^{\prime }(x)}=\underset{x\to +\infty }{\lim }\frac{-\frac{f^{\prime }(1/x)}{x^2}}{-\frac{g^{\prime }(1/x)}{x^2}}=\underset{x\to +\infty }{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}.$$所以, 根据前一版本的 L’Hôpital 法则, 我们有$$\underset{x\to +\infty }{\lim }\frac{f(x)}{g(x)}=\underset{x\to 0^{+}}{\lim }\frac{\tilde{f}(x)}{\tilde{g}(x)}=\underset{x\to +\infty }{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}.$$这就证明了命题.

$\square$

推论 16.3. $n⩾1$ 是整数, $f$ 和 $g$ 是区间 $(a,b)$ 上 $n$-次可微的实值函数. 假设对任意的 $0⩽k⩽n-1$, 都有$$\underset{x\to a^{+}}{\lim }{f}^{(k)}(x)=0,\underset{x\to a^{+}}{\lim }{g}^{(k)}(x)=0,$$并且极限 $\underset{x\to a^{+}}{\lim }\frac{f^{(n)}(x)}{g^{(n)}(x)}$ 存在 (可以是 $\pm \infty$) . 如果对 $x\in (a,b)$, $g^{(n)}(x)\ne 0$, 那么$$\underset{x\to a^{+}}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a^{+}}{\lim }\frac{f^{(n)}(x)}{g^{(n)}(x)}.$$

证明. 我们 $n$ 用归纳法就立即得到了证明, 但是每次都要检验导数不为零的条件: 由于 $f^{(n)}(x)\ne 0$, 根据 Darboux 介值定理, $f^{(n)}(x)$ 恒正或者恒负, 所以函数严格单调. 由于 $f^{(n-1)}(a)=0$, 所以 $f^{(n-1)}(x)$ 恒为正或者恒为负. 以此类推, 所有导数都非零.

$\square$

我们还有其它两个类型的 L’Hôpital 法则:

推论 16.4 (L’Hôpital 法则). 假设 $f$ 和 $g$ 是区间 $(a,b)$ 上的可微实值函数, 我们假设$$\underset{x\to a^{+}}{\lim }|f(x)|=\infty ,\underset{x\to a^{+}}{\lim }|g(x)|=\infty .$$我们假设对任意的 $x\in (a,b)$, $g^{\prime }(x)\ne 0$. 如果极限 $\underset{x\to a^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$ 存在 (可以是 $\pm \infty$) , 那么$$\underset{x\to a^{+}}{\lim }\frac{f(x)}{g(x)}=\underset{x\to a^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}.$$

推论 16.5 (L’Hôpital 法则). 实值函数 $f$ 和 $g$ 在区间 $(a,+\infty )$ 上可微并且$$\underset{x\to +\infty }{\lim }|f(x)|=\infty ,\underset{x\to +\infty }{\lim }|g(x)|=\infty .$$假设对任意的 $x\in (a,+\infty )$, $g^{\prime }(x)\ne 0$. 如果极限 $\underset{x\to +\infty }{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$ 存在 (可以是 $\pm \infty$) , 那么我们有$$\underset{x\to +\infty }{\lim }\frac{f(x)}{g(x)}=\underset{x\to +\infty }{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}.$$

这两个推论的证明我们留成本次作业.

L’Hôpital 法则可以用来计算极限:

例子. 我们举几个例子:

1)	计算 $\underset{x\to 0}{\lim }\frac{\sin x}{x}$: $$\underset{x\to 0}{\lim }\frac{\sin x}{x}=\underset{x\to 0}{\lim }\frac{\cos x}{1}=1.$$
2)	计算 $\underset{x\to 0}{\lim }\frac{e^x-x-1}{x^2}$: $$\underset{x\to 0}{\lim }\frac{e^x-x-1}{x^2}=\underset{x\to 0}{\lim }\frac{e^x-1}{2x}=\underset{x\to 0}{\lim }\frac{e^x}{2}=\frac{1}{2}.$$
3)	证明 $\underset{x\to \infty }{\lim }\frac{x^n}{e^x}=0$: $$\underset{x\to \infty }{\lim }\frac{x^n}{e^x}=\underset{x\to \infty }{\lim }\frac{n{x}^{n-1}}{e^x}=\underset{x\to \infty }{\lim }\frac{n(n-1)x^{n-2}}{e^x}=\cdots =\underset{x\to \infty }{\lim }\frac{n!}{e^x}=0.$$
4)	计算 $\underset{x\to \infty }{\lim }\frac{x}{\sqrt{x^2+1}}$. 第一次运用 L’Hôpital 法则, 我们就会有$$\underset{x\to \infty }{\lim }\frac{x}{\sqrt{x^2+1}}=\underset{x\to \infty }{\lim }\frac{1}{\frac{x}{\sqrt{x^2+1}}}=\underset{x\to \infty }{\lim }\frac{\sqrt{x^2+1}}{x}.$$再用一次就得到$$\underset{x\to \infty }{\lim }\frac{\sqrt{x^2+1}}{x}=\underset{x\to \infty }{\lim }\frac{x}{\sqrt{x^2+1}}.$$所以一直不会停止. 对于这个例子 L’Hôpital 法则并不好用.
5)	计算 $\underset{x\to 0}{\lim }\frac{\sin x}{e^x}$. 如果我们不检验 $f(x)$ 和 $g(x)$ 在 $0$ 处是否是零而直接运用 L’Hôpital 法则, 我们就会有$$\underset{x\to 0}{\lim }\frac{\sin x}{e^x}=\underset{x\to 0}{\lim }\frac{\cos x}{e^x}=1.$$这个结论自然是错误的!

Taylor 展开

L’Hôpital 法则只是一种计算极限的方法, 它之所以有用 (更多是做习题的时候) 主要因为它可以把求极限这种分析上的操作转化为求导数的问题, 而求导数的操作一般而言都是代数操作 (因为我们可以背过很多导数) . 然而, 对于微积分的学习, 这个法则似乎无关主旨, 我们应该尽量早的学习 Taylor 展开的技术, 这才是真正要紧的东西:

定理 16.6 (Taylor 展开公式: 用多项式逼近). 我们给出 Taylor 展开的三种不同余项的叙述:

1)	Peano 余项. 假设函数 $f:[a,b]\to \mathbb{R}$ (或者 $\mathbb{C}$) 在 $a$ 处的一直到 $n$-次导数 $f^{\prime }(a),\cdots ,f^{(n)}(a)$ 都存在. 那么, 当 $x\to a^{+}$ 时, 我们有$$f(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k+o((x-a{)}^n).$$
2)	Lagrange 余项. 假设函数 $f\in C^n([a,b])$ (在 $\mathbb{R}$ 或 $\mathbb{C}$ 中取值) , 特别地, $f$ 在 $a$ 处的 $n$-次导数 $f^{\prime }(a)$, $\cdots$, $f^{(n)}(a)$ 都存在. 如果 $f$ 在 $(a,b)$ 上 $n+1$ 次可导. 那么, 我们有$$f(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k+R_n(x),$$其中 $R_n(x)=\frac{f^{(n+1)}(\xi )}{(n+1)!}(x-a{)}^{n+1}$, $\xi \in [a,x]$ 由 $x$ 决定 (未必唯一) .
2)	Cauchy 余项. 假设函数 $f\in C^n([a,b])$ (在 $\mathbb{R}$ 或 $\mathbb{C}$ 中取值) , 特别地, $f$ 在 $a$ 处的 $n$-次导数 $f^{\prime }(a)$, $\cdots$, $f^{(n)}(a)$ 都存在. 如果 $f$ 在 $(a,b)$ 上 $n+1$ 次可导. 那么, 我们有$$f(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k+{\overline{R}}_n(x),$$其中 ${\overline{R}}_n(x)=\frac{f^{(n+1)}(\xi )}{n!}(x-\xi {)}^n(x-a)$, $\xi \in [a,x]$ 由 $x$ 决定 (未必唯一) .

注记. Peano 余项的公式只在 $a$ 的附近成立, 而 Lagrange 和 Taylor 的情况是整体的公式.

我们注意到当 $n=1$ 时, Peano 余项的公式就是导数的定义.

当 $n=0$ 时, Lagrange 余项的公式就是 Lagrange 中值定理.

另外, 如果要求 $f$ 是 $n$-次连续可微的并且 $n+1$ 次导数存在, 那么 Lagrange 余项 (或者 Taylor 余项) 的公式成立, 此时, 根据连续性, Peano 余项的公式明显成立.

证明.

1)	Peano 余项公式等价于证明$$\underset{x\to a^{+}}{\lim }\frac{f(x)-\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k}{(x-a{)}^n}=0.$$我们利用 L’Hôpital 法则逐次求导数 (容易验证该法则所要求的条件) : $$\begin{array}{rl}\underset{x\to a^{+}}{\lim }\frac{f(x)-\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k}{(x-a{)}^n}& =\cdots =\underset{x\to a^{+}}{\lim }\frac{f^{(n-1)}(x)-f^{(n-1)}(a)-f^{(n)}(a)(x-a)}{n!(x-a)}\\ & =\frac{1}{n!}\underset{x\to a^{+}}{\lim }(\frac{f^{(n-1)}(x)-f^{(n-1)}(a)}{x-a}-f^{(n)}(a))\\ & =0.\end{array}$$最后一步是利用导数的定义.
2)	将 $x$ 视作是固定的, 我们定义$$F(t)=\sum _{k=0}^n\frac{f^{(k)}(t)}{k!}(x-t{)}^k=f(t)+\sum _{k=1}^n\frac{f^{(k)}(t)}{k!}(x-t{)}^k.$$我们对 $t$ 求导数得到: $$\begin{array}{rl}{F}^{\prime }(t)& =f^{\prime }(t)+\sum _{k=1}^n\frac{f^{(k+1)}(t)}{k!}(x-t{)}^k+\sum _{k=1}^n\frac{(-1)f^{(k)}(t)}{(k-1)!}(x-t{)}^{k-1}\\ & =f^{\prime }(t)+\sum _{k=1}^n\frac{f^{(k+1)}(t)}{k!}(x-t{)}^k-\sum _{\ell =0}^{n-1}\frac{f^{(\ell +1)}(t)}{\ell !}(x-t{)}^{\ell }.\end{array}$$所以,$$F^{\prime }(t)=\frac{f^{(n+1)}(t)}{n!}(x-t{)}^n.$$现在考虑另一个关于 $t$ 的函数 (定义在 $[a,x]$ 上) : $$G(t)=(\frac{x-t}{x-a}{)}^{n+1}$$很明显, $G^{\prime }(t)$ 在 $(a,x)$ 上不是零. 根据 Cauchy 中值定理, 存在 $\xi \in (a,x)$, 使得$$\frac{F^{\prime }(\xi )}{G^{\prime }(\xi )}=\frac{F(x)-F(a)}{G(x)-G(a)}.$$即$$\frac{\frac{f^{(n+1)}(\xi )}{n!}(x-\xi {)}^n}{\frac{-(n+1)(x-\xi {)}^n}{(x-a{)}^{n+1}}}=\frac{F(x)-F(a)}{-G(a)}=-(F(x)-F(a))=-f(x)+\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k.$$整理即得 Lagrange 余项的公式.
3)	为了证明 Cauchy 余项的公式, 我们同样考虑上述的 $F(t)$, 但是我们将选取一个不同的 $G$: $$G(t)=\frac{x-t}{x-a}$$很明显, $G^{\prime }(t)$ 在 $(a,x)$ 上不是零. 根据 Cauchy 中值定理, 存在 $\xi \in (a,x)$, 使得$$\frac{F^{\prime }(\xi )}{G^{\prime }(\xi )}=\frac{F(x)-F(a)}{G(x)-G(a)}.$$即$$\frac{\frac{f^{(n+1)}(\xi )}{n!}(x-\xi {)}^n}{\frac{-1}{x-a}}=\frac{F(x)-F(a)}{-G(a)}=-(F(x)-F(a))=-f(x)+\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k.$$整理即得 Cauchy 余项的公式. $\square$

上面 Lagrange 余项的证明很有技巧性, (我) 很难理解. 如果有了积分作工具, 我们可以给出一个最自然的证明. 我们现在给出另一个证明: 我们知道, 当 $n=1$ 时 Lagrange 余项的公式是 Lagrange 中值定理, 我们下面利用中值定理证明的方法, 来给出一个相对自然的 (容易记住) 证明. 为此, 首先推广 Rolle 定理到高阶导数的情形:

引理 16.7. 假设 $f\in C^n([a,b])$ 并且在 $(a,b)$ 上 $n+1$ 次可导. 如果 $f$ 在 $a$ 处的 $n$-次导数全为零, 即 $f^{\prime }(a)=0,\cdots ,f^{(n)}(a)=0$ 并且 $f(a)=f(b)$, 那么存在 $x_0\in (a,b)$, 使得 $f^{(n+1)}(x_0)=0$.

证明. 我们只要不停地用 Rolle 中值定理即可: 由于 $f(a)=f(b)$, 根据 Rolle 中值定理, 存在 $x_1\in (a,b)$, 使得 $f^{\prime }(x_1)=0$; 由于 $f^{\prime }(a)=f^{\prime }(x_1)=0$, 再用 Rolle 中值定理, 我们就找到 $x_2\in (a,x_1)$, 使得 $f^{\prime \prime }(x_2)=0$; 如此下去, 我们得到 $f^{\prime \prime }(x_2)=f^{\prime \prime \prime }(x_3)=\cdots =0$. 最后一步, 就得到了 $f^{(n+1)}(x_{n+1})=0$. 选取 $x_0=x_{n+1}$ 即可.

$\square$

我们仿照 Lagrange 中值定理的证明: 先构造多项式 $P(x)$, 使得 $P(a)=f(a)$, $P^{\prime }(a)=f^{\prime }(a)$, $\cdots$, $P^{(n)}(a)=f^{(n)}(a)$, 比如, 我们取$$P_n(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k.$$

练习. 证明, 如果多项式 $P(x)$ 的次数 $⩽n$, 那么满足上面条件的多项式是唯一的.

为了应用高阶导数的 Rolle 定理, 我们对 $P_n(x)$ 略加改造: 选取 $\lambda \in \mathbb{R}$ (存在且唯一) , 使得 $P(b)=f(b)$, 其中 $P(x)=P_n(x)+\lambda (x-a{)}^{n+1}$, $\lambda =\frac{f(b)-P_n(b)}{(b-a{)}^{n+1}}$. 我们现在考虑函数 $f(x)-P(x)$, 它满足高阶导数 Rolle 定理的条件, 所以存在 $c\in (a,b)$, 使得$$f^{(n+1)}(c)-P^{(n+1)}(c)=0.$$利用 $\lambda$ 的表达式, 我们得到$$f^{(n+1)}(c)-(n+1)!\frac{f(b)-P_n(b)}{(b-a{)}^{n+1}}=0.$$如果改写为 $c=\xi$, $b=x$, 这就是 Lagrange 余项的 Taylor 公式.

注记. 满足 Peano 余项的 Taylor 展开公式是唯一的, 即若假设函数 $f:[a,b]\to \mathbb{R}$ (或者 $\mathbb{C}$) 在 $a$ 处的一直到 $n$-次导数 $f^{\prime }(a),\cdots ,f^{(n)}(a)$ 都存在. 那么, 如果存在次数不超过 $n$ 的多项式 $P(x)$, 使得当 $x\to a^{+}$ 时, 我们有$$f(x)=P(x)+o((x-a{)}^n).$$那么, $$P(x)=\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k.$$令 $Q(x)=P(x)-\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k$, 实际上按照 Peano 余项的 Taylor 展开公式, 我们必然有$$\underset{x\to a^{+}}{\lim }\frac{Q(x)}{(x-a{)}^n}=\underset{x\to a^{+}}{\lim }\frac{P(x)-{\sum }_{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k}{(x-a{)}^n}=0.$$由于 $\mathrm{deg}Q⩽n$, 所以 $Q=0$.

由此可见, 如果限定的多项式的次数 $⩽n$, 那么 $\sum _{k=0}^n\frac{f^{(k)}(a)}{k!}(x-a{)}^k$ 是在 $a$ 附近对 $f(x)$ 最佳的逼近.

例子. 我们有两个比较极端的例子:

1)	正弦函数 $\sin x$: 我们可以在 $x=0$ 处计算其导数 (偶数次的导数都是零) , 从而得到它的 Peano 展开为: $$\sin x=\sum _{k=0}^n\frac{(-1{)}^k{x}^{2k+1}}{(2k+1)!}+o(|x{|}^{2n+2}).$$这和 $\sin x$ 的解析表达式之间似乎是一致的 (我们暂时不研究这一点) .
2)	我们考虑如下的函数$$f(x)=\{\begin{array}{ll}{e}^{-\frac{1}{x^2}},& x>0;\\ 0,& x⩽0\end{array}$$那么函数在 $0$ 点处的所有导数都是 $0$, 从而对任意的 $n⩾1$, $$f(x)=o(|x{|}^n).$$当然, $f(x)$ 不是零.