最速降线问题
从点
(x,f(x)) 到
(x+Δx,f(x+Δx)) 的距离是
1+f′(x)2Δx. 根据重力势能到动能的转化 (能量守恒) , 我们知道
21mv2=−mGf(x).在
(x,f(x)) 处, 小球的速度应该是
−2Gf(x), 所以从
(x,f(x)) 到
(x+Δx,f(x+Δx)) 所需要的时间是
Δt=−2Gf(x)1+f′(x)2Δx这样, 如果曲线
γs 由函数
fs(x)=f(x,s) 给出, 即
γs:x∈[0,a]↦(x,fs(x)).小球经过整个曲线需要的时间为
T(s)=∫0a−2Gf(x,s)1+f′(x,s)2dx.其中,
f′ 指的是对
f(x,s) 的
x 变量求导数. 为了保证曲线的两个端点是固定的, 我们还要求
f(0,s)≡0, f(a,s)≡−h.对于最速降线
f0 而言, 我们必然有
dsdT(s)∣∣s=0=0.为此, 我们假设
L(f,f′)=−2Gf(x,s)1+f′(x,s)2, 即在函数
L(X,V)=−2GX1+V2中代换变量
X=f,
V=f′. 此时, 我们有 (我们总是假设足够的光滑性使得积分与导数可以交换) :
dsdT(s)=∫0adsd(L(fs,fs′))dx=∫0a(dXdL)(fs,fs′)dsdf(x,s)+(dVdL)(fs,fs′)dsdf′(x,s)dx最后一项中, 我们利用两个导数可以交换 (下学期) , 所以
dsdf′(x,s)=(dsdf(x,s))′. 令
s=0 并记
f=f0, 我们就有
dsdT(s)∣∣s=0=∫0a(dXdL)(f,f′)dsdf(x,0)+(dVdL)(f,f′)(dsdf(x,s)∣∣s=0)′dx=∫0a((dXdL)(f,f′)−dxd(dVdL)(f,f′))dsdf(x,0)dx.最后一步分部积分的过程中, 我们用到了
f(0,s)≡0,
f(a,s)≡−h, 从而
dsdf(0,s)≡0, dsdf(a,s)≡0.另外, 对任意的函数
g (
g(0)=g(a)=0) , 我们通过定义
f(x,s)=f(x)+sg(x) 就可以使得
dsdf(x,s)∣∣s=0=g(x).所以, 通过选取
g(x)=φ(x)[(dXdL)(f,f′)−dxd(dVdL)(f,f′)],我们就得到了
f 必须满足的方程 (这被称作是 Euler-Lagrange 方程) :
(dXdL)(f,f′)−dxd((dVdL)(f,f′))=0.假设上述方程成立, 那么
dxd((VdVdL−L)(f,f′))=dxd(f′dVdL(f,f′)−L(f,f′))=f′′dVdL(f,f′)+f′dxd(dVdL(f,f′))−f′dXdL(f,f′)−f′′dVdL(f,f′)=0.这表明, 存在常数
C, 使得
(VdVdL−L)(f,f′)≡C按照定义, 我们有
dXdL=G(−2GV)23(1+V2)21, dVdL=(−2GX(1+V2))21V.所以,
(−2Gf(1+(f′)2))21(f′)2−−2Gf1+(f′)2=C, ⇔ f(1+(f′)2)=−C1.我们令
f(x)=−g(x), 那么, 我们就有
g′(x)=gC1−g如果把
g 看作参数,
x=x(g), 那么, 根据反函数的导数的计算, 我们有
dgdx=C1−gg从而, 作为原函数, 我们有
x(t)=∫C1−ttdt.为了能积分出这个函数, 我们做变量替换
t=C1sin2θ,从而,
x(θ)=2C1∫tanθ⋅cosθ⋅sinθdθ=C1(θ−21sin(2θ)).这样子, 我们就得到了这条曲线的参数方程 (原函数差一个常数
C2)
θ↦(2C1(2θ−sin(2θ))+C2,−2C1(1−cos(2θ)))重新参数化之后, 我们得到一条曲线
γ:[θ1,θ2]→R2, θ↦(c(θ−sinθ)+C,−c(1−cosθ))这种曲线叫做被称作是摆线或者旋轮线. 我们注意到, 初始时刻
y(θ1)=0, 所以,
cosθ1=1, 这表明
θ1=2kπ,
C=−2ckπ, 通过再次调整
θ↦θ−2kπ, 我们可以假设
θ1=0,
C=0, 所以我们要找的参数曲线为
γ:[0,Θ]→R2, θ↦(c(θ−sinθ),−c(1−cosθ))从而,
c(Θ−sinΘ)=a, −c(1−cosΘ)=−h可以确定
Θ∈[0,2π] 和
c.
考虑摆线γ:[0,2π]→R2, θ↦(c(θ−sinθ),−c(1−cosθ)).
那么, 从任意一点
γ(θ0) 出发的小球滚动到
γ(π)=(cπ,−2c) 的时间都是一样的.
证明. 实际上, 小球在
γ(θ) 到
γ(θ+Δθ) 处要经过的距离为:
Δ=∣γ′(θ)∣Δθ=c2−2cosθΔθ小球的速度为:
v=2Gc(cosθ0−cosθ).所以, 从
γ(θ0) 滑到底一共需要
T(θ0)=Gc∫θ0πcosθ0−cosθ1−cosθdθ=Gc∫θ0πcos2(2θ0)−cos2(2θ)sin(2θ)dθ我们可以令
s=cos(2θ) 进行换元积分, 据此, 得到
T(θ0)≡πGc.
积分中值定理
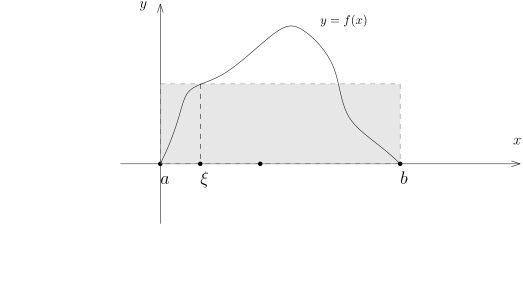
[a,b] 是有界闭区间, f,g∈R([a,b]) 是实值 Riemann 可积函数. 我们假设对任意的 x∈[a,b], g(x)⩾0. 令m=x∈Iinff(x), M=x∈Isupf(x).那么, 存在 ℓ∈[m,M], 使得∫abfg=ℓ∫abg.特别地, 如果进一步要求 f 是连续函数, 那么存在 ξ∈[a,b], 使得∫abfg=f(ξ)∫abg.
证明. 由于 m⩽f(x)⩽M, 根据 g⩾0 以及积分保持不等号的性质, 我们有m∫abg⩽∫abfg⩽M∫abg.如果 ∫abg=0, 显然存在 ℓ∈[m,M] 使得命题成立; 如果 ∫abg=0, 由于 g⩾0, 所以 g 在一个零测集之外恒为 0, 从而 fg 在一个零测集之外都是 0, 从而 ∫abfg=0, 所以 ℓ 可以任意选.
如果
f 是连续的, 所以
f 在
[a,b] 可以取到最大值
M 和最小值
m, 即有
x1,x2∈[a,b], 使得
f(x1)=m,
f(x2)=M, 根据连续函数的中值定理, 存在
x1 与
x2 之间的数
ξ, 使得
f(ξ)=ℓ.
假设 f 是连续函数, 那么存在 ξ∈[a,b], 使得 ∫abf=f(ξ)(b−a).