回顾: Fubini 定理 我们上一周证明了 Fubini 定理, 它讲的是, 给定 σ ( X , A , μ ) ( Y , B , ν ) X × Y f f X × Y ∫ X × Y f ( x , y ) d μ ⊗ ν = ∫ X ( ∫ Y f ( x , y ) d ν ( y ) ) d μ ( x ) = ∫ Y ( ∫ X f ( x , y ) d μ ( x ) ) d ν ( y ) .
除了在计算积分时可以降维之外, Fubini 定理还有其它的应用: 它表明在 X Y ∫ X ( ∫ Y f ( x , y ) d ν ( y ) ) d μ ( x ) = ∫ Y ( ∫ X f ( x , y ) d μ ( x ) ) d ν ( y ) ,
f ( X , A , μ ) f : X → [ 0 , ∞ ) R ⩾ 0 g : [ 0 , ∞ ) → [ 0 , ∞ ) g ( 0 ) = 0 ∫ X g ∘ fd μ = ∫ [ 0 , ∞ ) g ′ ( t ) μ ({ x ∣ f ( x ) ⩾ t }) d t . ∫ X fd μ = ∫ [ 0 , ∞ ) μ ( { x ∣ f ( x ) ⩾ t } ) d t .
证明. 根据 Newton–Leibiniz 公式, 我们有
∫ X g ∘ fd μ = ∫ X ( g ( f ( x )) − g ( 0 ) ) d μ = ∫ X ( ∫ [ 0 , f ( x )] g ′ ( x ) d s ) d μ = ∫ X ( ∫ [ 0 , ∞ ) g ′ ( s ) 1 [ 0 , f ( x )] ( s ) d s ) d μ . 根据正函数版本的 Fubini 定理, 我们有
∫ X g ∘ fd μ = ∫ X × [ 0 , ∞ ) ( g ′ ( s ) 1 [ 0 , f ( x )] ( s ) ) d s ⊗ d μ = ∫ [ 0 , ∞ ) ( ∫ X g ′ ( s ) 1 [ 0 , f ( x )] ( s ) d μ ) d s = ∫ [ 0 , ∞ ) g ′ ( s ) μ ({ x ∣ f ( x ) ⩾ s }) d s . 特别地, 当
g ( s ) = s 时, 我们就得到了第二个等式.
换元积分公式 换元积分公式是计算积分的另一个重要手段, 为了给出一个相对漂亮的表述, 我们先进行一些抽象的表述.
给定测度空间 ( X , A , μ ) μ σ X ρ : X → [ 0 , ∞ ] . ρ N ∈ A μ ( N ) = 0 x ∈ / N ρ ( x ) < ∞. ν : = ρ μ : A → [ 0 , ∞ ] , A ↦ ∫ X ρ ( x ) 1 A ( x ) d μ ( x ) .
如果 A , B ∈ A A ∩ B = ∅ ν ( A ∪ B ) = ∫ X ρ ( x ) 1 A ∪ B ( x ) d μ ( x ) = ∫ X ρ ( x ) 1 A ( x ) d μ ( x ) + ∫ X ρ ( x ) 1 B ( x ) d μ ( x ) = ν ( A ) + ν ( B ) . ν 是加性函数.
我们再任意选取单调上升的序列 { A j } j ⩾ 1 ⊂ A A j ↗ A Beppo Levi 定理, 我们有ν ( A j ) = ∫ X ρ ⋅ 1 A i d μ → ∫ X ρ ⋅ 1 A d μ = ν ( A ) , ν
我们还可以说明这是一个 σ ρ μ σ { X p } p ⩾ 1 ⊂ A X p ↗ X p μ ( X p ) < ∞ Y p = { x ∣ ρ ( x ) ⩽ p } ∩ X p . { Y p } p ⩾ 1 ⊂ A Y p ↗ X ν ( Y p ) ⩽ ∞ ν ( Y p ) = ∫ X ρ ( x ) 1 Y p ( x ) d μ ( x ) ⩽ ∫ X p 1 X p ( x ) d μ ( x ) = p μ ( X p ) < ∞.
给定 σ ( X , A , μ ) ρ ν = ρ μ ( X , A ) σ ν ( X , A , μ ) 以 ρ 为密度的测度 .
对于以
ρ 为密度的测度的测度
ν 以及
( X , A , μ ) 上的可测函数. 我们可以证明
f ρ 对于测度
μ 可积当且仅当
f 对于测度
ν 可积, 并且此时有
∫ X f ( x ) d ν ( x ) = ∫ X f ( x ) ρ ( x ) d μ ( x ) . 我们把这个性质的证明留作习题.
我们先证明一个抽象版本的换元积分公式 (漂亮但是用途不大) . 给定测度空间 ( X , A , μ ) ( Y , B ) Φ : ( X , A , μ ) → ( Y , B ) . μ Φ ( Y , B ) Φ ∗ μ B ∈ B ( Φ ∗ μ ) ( B ) = μ ( Φ − 1 ( B ) ) . σ Φ : R 2 → R , ( x , y ) ↦ x . R 1 Φ ∗ m 2 σ A ⊂ R 1 m 1 ( A ) > 0 ( Φ ∗ μ ) ( A ) = + ∞
给定测度空间 ( X , A , μ ) ( Y , B ) ( Y , B ) f Φ : ( X , A , μ ) → ( Y , B ) . f ( Y , B , Φ ∗ ( μ )) ( f ∘ Φ ) ( x ) ( X , A , μ ) ∫ Y f ( y ) d ν ( y ) = ∫ X ( f ∘ Φ ) ( x ) d μ ( x ) . ν = Φ ∗ μ
证明. 这个证明过程只需要照章办事: 首先, 如果
f = 1 B 是示性函数, 其中
B ∈ B , 那么,
∫ Y 1 B d ν = ν ( B ) = μ ( Φ − 1 ( B )) = ∫ X 1 Φ − 1 ( B ) ( x ) d μ ( x ) = ∫ X 1 B ∘ Φ d μ . 所以, 命题明显成立. 所以, 通过线性命题对一切简单正函数上式都成立. 对于一般的正函数,
f , 我们选取单调上升的简单正
{ f i } i ⩾ 1 序列, 使得它们逐点收敛到
f . 那么, 根据 Beppo Levi 定理, 我们有
∫ Y fd ν = i → ∞ lim ∫ Y fd ν = i → ∞ lim ∫ X f i ∘ Φ d μ = ∫ X f ∘ Φ d μ . 从而, 该定理对正函数也成立. 特别地, 由于
∣ f ∘ Φ∣ = ∣ f ∣ ∘ Φ , 从而
f 在
( Y , B , Φ ∗ ( μ )) 上可积当且仅当
( f ∘ Φ ) ( x ) 在
( X , A , μ ) 上可积. 为了验证可积函数的等式, 我们只要将函数分解为正负部分或这实虚部利用线性即可, 我们略去冗长无聊的细节.
我们现在正式进入 R n
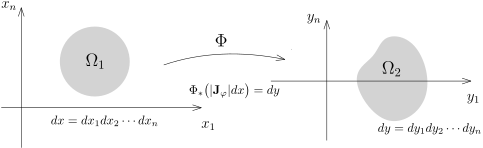
假定 Ω 1 Ω 2 R n Φ : Ω 1 → Ω 2 C 1 Φ Φ − 1 C 1 Φ Φ : Ω 1 → Ω 2 , ( x 1 , ⋯ , x n ) ↦ ( Φ 1 ( x 1 , ⋯ , x n ) , ⋯ , Φ n ( x 1 , ⋯ , x n ) ) Φ J Φ ( x 1 , ⋯ , x n ) = ∣ ∣ Jac ( Φ ) ( x 1 , ⋯ , x n ) ∣ ∣ = det ( ∂ x j ∂ Φ i ) ∣ ∣ x = ( x 1 , ⋯ , x n ) .
假定 Ω 1 Ω 2 R n Φ : Ω 1 → Ω 2 d x d y Ω 1 Ω 2
对于 Ω 2 f : Ω 2 → C Ω 2 d y f ∘ Φ Ω 1 ∣ J Φ ( x ) ∣ d x Φ ∗ ( ∣ J Φ ∣ d x ) = d y . Ω 2 d y f ∫ Ω 2 f ( y ) d y = ∫ Ω 1 ( f ∘ Φ ) ( x ) ∣ J Φ ( x ) ∣ d x .
记住 (不是证明) 上面的公式可以用如下的窍门: 将 y = Φ ( x ) f ( y ) ( f ∘ Φ ) ( x ) d y = d Φ ∘ d x d Φ ∣ J Φ ( x ) ∣
换元积分公式是本学期最困难的证明之一, 我们要分若干步骤来完成. 在考察一般的微分同胚之前, 我们先研究比较特殊的一种微分同胚: 仿射变换.
我们假定 Φ Φ : Ω 1 → Ω 2 , x ↦ Φ ( x ) = A ⋅ x + x 0 , x ∈ R n x 0 ∈ R n A n × n Φ − 1 ( y ) = A − 1 ⋅ y − A − 1 ⋅ x 0 .
如果 A Φ τ x 0 Ω 2 = τ x 0 Ω 1 ( τ x 0 ) ∗ m = m . ∣ ∣ J Φ ∣ ∣ = 1 ∫ Ω 1 f ∘ Φ d x = ∫ Ω 1 f ( x + x 0 ) d x = ∫ Ω 2 f ( y ) d ( τ x 0 ) ∗ m = ∫ Ω 2 f ( y ) d y . f Ω 1 Φ x 0 = 0
我们现在假设Φ ( x ) = A ⋅ x . A A = O ⋅ S , O S 1 O S 测度在正交变换下不变 (作业五 A11)) , 我们可以照搬上述关于平移的论证, 通过对 Φ A A R Λ
根据上面的讨论, 最终, 我们只要对如下的映射来证明命题即可: Φ : ( x 1 , ⋯ , x n ) ↦ ( λ 1 x 1 , ⋯ , λ n x n ) , λ 1 , ⋯ , λ n
我们要用 Fubini 公式降低维数 n n = 1 ρ λ : R 1 → R 1 , x ↦ λ x , λ > 0 ( ρ λ ) ∗ m = λ − 1 m . Ω 2 = ρ λ ( Ω 1 ) ∫ Ω 1 f ( λ x ) d x = ∫ Ω 2 f ( y ) ( ρ λ ) ∗ m = λ − 1 ∫ Ω 2 f ( y ) d y . n d x ˉ d x 1 ⋯ d x n − 1 d y ˉ d y 1 ⋯ d y n − 1 = = = = ∫ Ω 1 f ( λ 1 x 1 , ⋯ , λ n x n ) d x ˉ ⊗ d x n ∫ R n f ( λ 1 x 1 , ⋯ , λ n x n ) 1 Ω ( x 1 , ⋯ , x n ) d x ˉ ⊗ d x n ∫ R ( ∫ R n − 1 f ( λ 1 x 1 , ⋯ , λ n x n ) 1 Ω 1 ( x 1 , ⋯ , x n ) d x ˉ ) d x n ( λ 1 ⋯ λ n − 1 ) − 1 ∫ R ( ∫ R n − 1 f ( y 1 , ⋯ , y n − 1 , λ n x n ) 1 Ω 1 ( λ 1 y 1 , ⋯ , λ n − 1 y n − 1 , x n ) d y ˉ ) d x n ( λ 1 ⋯ λ n ) − 1 ∫ Ω 2 f ( y ) d y . ( λ 1 ⋯ λ n ) − 1 J Φ
综上所属, 当 Φ R n
我们在 R n B ( R n ) μ
∙ 如果 K ⊂ R n μ ( K ) < ∞
那么, 对于任意的 A ∈ B ( R n ) ε > 0 U A A F F ⊂ A ⊂ U μ ( U − F ) < ε .
证明. 我们定义A = { A ∈ B ( R n ) ∣ ∣ 对任意 ε > 0 ,存在开集 U ⊃ A 和闭集 F ⊂ A ,使得 μ ( U − F ) < ε } . K K ∈ A F = K k ∈ Z ⩾ 1 U k = { x ∈ R n ∣ ∣ d ( x , K ) < k 1 } . d ( x , K ) d ( x , K ) = y ∈ K inf d ( x , y ) . K K → R , y ↦ d ( x , y ) x ∈ K d ( x , K ) = 0 K k U k μ ( U 1 ) < ∞ U k ↘ K μ ( U k ) → μ ( K ) k 0 μ ( U k 0 − K ) < ε U = U k 0
为了证明这个命题, 我们要说明 A A σ
很明显, ∅ ∈ A A A ∈ A ε > 0 U ⊃ A F ⊂ A μ ( U − F ) < ε A c F c ⊃ A c ⊃ U c F c U c μ ( F c − U c ) = μ ( U − F ) < ε . A c ∈ A
现在来证明 A { A i } i ⩾ 1 ⊂ A A i ⩾ 1 U i F i F i ⊂ A i ⊂ U i , μ ( U i − F i ) < 2 i ε . F = i ⩾ 1 ⋃ F i , U = i ⩾ 1 ⋃ U i , F ⊂ i ⩾ 1 ⋃ A i ⊂ U , μ ( U − F ) ⩽ i ⩾ 1 ∑ μ ( U i − F i ) < i ⩾ 1 ∑ 2 i ε = ε . U F F
测度 μ B ( R n ) G = i ⩾ 1 ⋃ F i ε > 0 F ⊂ G μ ( G − F ) < ε .
分两种情况来证明引理:
1)
G μ ( G ) < ∞
对任意的 j ⩾ 1 F j = i ⩽ j ⋃ F i . F j ↗ G j → ∞ lim F j = G j → ∞ μ ( G − F j ) → 0 F = F k 0 k 0
2)
G μ ( G ) = ∞
我们考虑 G G k = G ∩ { x ∈ R n ∣ ∣ k − 1 ⩽ ∣ x ∣ ⩽ k } . μ ( G k ) < ∞ G k G k = i ⩾ 1 ⋃ G k ∩ F i k ⩾ 1 H k ⊂ G k μ ( G k − H k ) < 2 k ε . F = k ⩾ 1 ⋃ H k . μ ( G − F ) ⩽ k ⩾ 1 ∑ μ ( G k − H k ) < ε . F 为闭集, 我们现在利用分解 G = k ⩾ 1 ⋃ G k k , k ′ ∣ k − k ′ ∣ ⩾ 2 G k ∩ G k ′ = ∅ F G k ∪ G k + 1 H k ∪ H k + 1 F
我们现在正式开始换元积分公式的证明.
换元积分公式的证明. 我们分成五个步骤来完成这一任务:
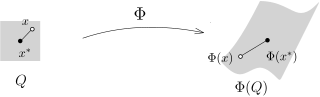
第一步 , 正方体的体积在 Φ Q h > 0 m ( Φ ( Q )) ⩽ ( x ∈ Q sup ∥ Jac ( Φ ) ( x ) ∥ ) n m ( Q ) , x = ( x 1 , ⋯ , x n ) ∈ R n n × n A = ( A ij ) ∥ x ∥ = i ⩽ n sup ∣ x i ∣ , ∥ A ∥ = i ⩽ n sup ( j = 1 ∑ n ∣ A ij ∣ ) .
我们对 Φ x ∗ Q x Q i ⩽ n Φ i ( x ) − Φ i ( x ∗ ) = j ⩽ n ∑ ∂ x j ∂ Φ i ( ξ i ) ( x j − x j ∗ ) , ξ i 为线段 x x ∗ 上的一点 (从而, ξ i ∈ Q ∥Φ ( x ) − Φ ( x ∗ ) ∥ = i ⩽ n sup ∣ Φ i ( x ) − Φ i ( x ∗ ) ∣ ⩽ L a g r an g e i sup j ⩽ n ∑ ∣ ∂ x j ∂ Φ i ( ξ j ) ∣∣ ( x j − x j ∗ ) ∣ ⩽ ∥ x − x ∗ ∥ i ⩽ n sup j ⩽ n ∑ ∣ ∂ x j ∂ Φ i ( ξ j ) ∣ ⩽ 2 h x ∈ Q sup ∥ Jac ( Φ ) ( x ) ∥. ∥ x − x ∗ ∥ ⩽ 0.5 × h Φ ( Q ) Φ ( x ∗ ) x ∈ Q sup ∥ Jac ( Φ ) ( x ) ∥ h x ∈ Q sup ∥ Jac ( Φ ) ( x ) ∥ n m ( Q )
第二步 , 假定 Q m ( Φ ( Q )) ⩽ ∫ Q ∣ J Φ ( x ) ∣ d x
由于 Φ C 1 Q → R n 2 , x ↦ Jac ( Φ ) ( x ) ε > 0 Q Q i i ⩽ N Q i i x , x ′ ∈ Q i ∥ ( Jac Φ ( x ′ ) ) − 1 ⋅ Jac Φ ( x ) ∥ < ( 1 + ε ) n 1 .
现在选定一个小正方体
Q i 以及一个点
q 0 ∈ Q i , 我们对映射
( Jac Φ ( q 0 ) ) − 1 ∘ Φ 应用第一步的结论:
m ( ( Jac Φ ( q 0 ) ) − 1 ( Φ ( Q i )) ) = m ( ( Jac Φ ( q 0 ) ) − 1 ∘ Φ ( Q i ) ) ⩽ ( x ∈ Q i sup ∥ ( ( Jac Φ ( q 0 ) ) − 1 ∘ Jac Φ ( x ) ∥ ) n m ( Q i ) ⩽ ( 1 + ε ) m ( Q i ) . 利用仿射变换的换元积分公式, 我们有
m ( Φ ( Q i )) = m ( ( Jac Φ ( q 0 ) ) ∘ ( Jac Φ ( q 0 ) ) − 1 ∘ Φ ) ( Q i ) ) = ∣ J Φ ( q 0 ) ∣ m ( ( Jac Φ ( q 0 ) ) − 1 ∘ Φ ) ( Q i ) ) ⩽ ( 1 + ε ) ∣ J Φ ( q 0 ) ∣ m ( Q i ) . 现在允许
q 0 变化, 对上式两边在
Q i 上积分, 我们得到
m ( Φ ( Q i )) m ( Q i ) ⩽ ( 1 + ε ) m ( Q i ) ∫ Q i ∣ J Φ ( x ) ∣ d x , 从而 (约掉共同的因子)
m ( Φ ( Q i )) ⩽ ( 1 + ε ) ∫ Q i ∣ J Φ ( x ) ∣ d x . 另外, 这些小正方体
Q i 内部两两不相交, 从而
Φ ( Q i ) 内部两两不相交, 并且对任意的
i 和
j ,
Q i ∩ Q j 和
Φ ( Q i ∩ Q j ) 都是零测集 (零测集在微分同胚下的像还是零测集) . 下面我们对
Q i 的指标求和来得到
Q 上的积分:
m ( Φ ( Q )) = i ∑ m ( Φ ( Q i )) ⩽ i ∑ ( 1 + ε ) ∫ Q i ∣ J Φ ( x ) ∣ d x = ( 1 + ε ) ∫ ⋃ i Q i ∣ J Φ ( x ) ∣ d x = ( 1 + ε ) ∫ Q ∣ J Φ ( x ) ∣ d x . 令
ε → 0 , 这完成了第二步的证明.
第三步 , U ⊂ Ω 1 m ( Φ ( U )) ⩽ ∫ U ∣ J Φ ( x ) ∣ d x .
我们已经证明过每个开集 U Q i U = i = 1 ⋃ ∞ Q i Q i 的内部两两不交 (利用 2 − k m ( Φ ( U )) = N → ∞ lim m ( i ⩽ N ⋃ Φ ( Q i )) ⩽ N → ∞ lim i ⩽ N ∑ m ( Φ ( Q i )) ⩽ i = 1 ∑ ∞ ∫ Q i ∣ J Φ ( x ) ∣ d x = ∫ U ∣ J Φ ( x ) ∣ d x .
第四步 , B ⊂ Ω 1 m ( Φ ( B )) ⩽ ∫ B ∣ J Φ ( x ) ∣ d x .
我们假设 ∫ B ∣ J Φ ( x ) ∣ d x < ∞ μ = ∣ J Φ ( x ) ∣ d x . ∣ J Φ ( x ) ∣ U B ⊂ U ⊂ Ω 1 μ ( U ) ⩽ ( 1 + ε ) μ ( B ) . ∫ U ∣ J Φ ( x ) ∣ d x ⩽ ( 1 + ε ) ∫ B ∣ J Φ ( x ) ∣ d x . m ( Φ ( B )) ⩽ m ( Φ ( U )) ⩽ ∫ U ∣ J Φ ( x ) ∣ d x ⩽ ( 1 + ε ) ∫ B ∣ J Φ ( x ) ∣ d x . ε → 0
第五步 , f Ω 1 ∫ Ω 2 f ( y ) d y = ∫ Ω 1 ( f ∘ Φ ) ( x ) ∣ J Φ ( x ) ∣ d x .
我们首先来证明不等式: ∫ Ω 2 f ( y ) d y ⩽ ∫ Ω 1 ( f ∘ Φ ) ( x ) ∣ J Φ ( x ) ∣ d x . f = 1 B B { f i } i ⩾ 1 f ∫ Ω 2 f ( y ) d y = i → ∞ lim ∫ Ω 2 f i ( y ) d y ⩽ i → ∞ lim ∫ Ω 1 ( f i ∘ Φ ) ( x ) ∣ J Φ ( x ) ∣ d x = ∫ Ω 1 ( f ∘ Φ ) ( x ) ∣ J Φ ( x ) ∣ d x . Φ Ψ = Φ − 1 ∫ Ω 1 ( f ∘ Φ ) ( x ) ∣ J Φ ( x ) ∣ d x ⩽ ∫ Ω 2 ( f ∘ Φ ∘ Ψ ) ( y ) ∣ J Φ ( Ψ ( y )) ∣∣ J Ψ ( y ) ∣ d y = ∫ Ω 2 f ( y ) d y . ∣ J Φ ( Ψ ( y )) ∣∣ J Ψ ( y ) ∣ = 1
第六步 , 对于一般可积函数换元积分公式也成立. 我们只需要把函数拆为正负和实部虚部的和, 利用线性即可. 这就完成了定理的证明.
在 1 维 Riemann 积分情形下, 换元积分公式的表达有所不同. 假设 φ : [ a , b ] → [ c , d ] C 1 ∫ φ ( a ) φ ( b ) f ( y ) d y = ∫ a b f ( φ ( x )) φ ′ ( x ) d x . φ ∫ φ ( a ) φ ( b ) f ( y ) d y = − ∫ φ ( b ) φ ( a ) f ( y ) d y .