分布理论是法国数学家 Laurent M. Schwartz 在上个世纪四十年代引入的, 他在 1950 出版了 Théorie des distributions 一书总结了分布理论的精要与应用, 这项工作也是他获得 1950 年 Fields 奖的核心贡献. 中文分布 二字是书名中 distributions 的直译, 却没有说明这个理论究竟讲了什么. Schwartz 在分布理论方面的第一篇论文的题目可以解答这个疑惑: 这篇文章是 Généralisation de la notion de fonction, de dérivation, de transformation de Fourier et applications mathématiques et physiques , 即对函数、微分和 Fourier 变换的推广及在数学和物理中的应用. 我们在第一学年已经详细地学习了函数、微分和 Fourier 变换, 这个学期就秉承 Schwartz 的观点通过对之前概念的推广去欣赏分析学在数学和物理中的应用.
分布的定义与例子 如果不加说明, 我们总假设 Ω ⊂ R n n ⩾ 1 K ⊂ R n C K ∞ ( Ω ) Ω K C K ∞ ( Ω ) = { f ∈ C ∞ ( Ω ) ∣ ∣ supp ( f ) ⊂ K } . α = ( α 1 , ⋯ , α n ) ∂ α φ ∂ x 1 α 1 ∂ x 2 α 2 ⋯ ∂ x n α n φ , ∂ x i α i = ∂ x i α i ∂ α i ∣ α ∣ = i = 1 ∑ n α i .
我们用 D ( Ω ) = C 0 ∞ ( Ω ) Ω 试验函数空间 . 按照定义, 对于任意的 φ ∈ D ( Ω ) K ⊂ Ω R n f ∣ ∣ Ω − K ≡ 0 x ∈ Ω − K f ( x ) = 0
在空间 D ( Ω ) 规定 如下的收敛性 (拓扑) : 给定函数序列 { φ p } p ⩾ 1 ⊂ D ( Ω ) 收敛到 0 ∈ D ( Ω ) φ p ⟶ D ( Ω ) 0
1)
存在紧集 K ⊂ Ω p ⩾ 1 supp ( φ p ) ⊂ K
2)
对每个多重指标 α { ∂ α φ p } p ⩾ 1 K 0 p → ∞ lim ∥ ∂ α φ p ∥ L ∞ ( K ) = 0.
所谓 Ω 分布 (也称作广义函数 ) 指的是 D ( Ω ) u : D ( Ω ) → C , φ ↦ ⟨ u , φ ⟩ ,
1)
对任意的 φ , ψ ∈ D ( Ω ) α , β ∈ C ⟨ u , α φ + β ψ ⟩ = α ⟨ u , φ ⟩ + β ⟨ u , ψ ⟩ .
2)
对任意的紧集 K ⊂ Ω p C p C K φ ∈ C K ∞ ( Ω ) ∣ ⟨ u , φ ⟩ ∣ ⩽ C ∣ α ∣ ⩽ p sup ∥ ∂ α φ ∥ L ∞ ( K ) .
如果上述的 p K p u 阶 .
我们用 D ′ ( Ω ) Ω { u p } p ⩾ 1 ⊂ D ′ ( Ω ) 0 ∈ D ′ ( Ω ) 0 u p ⟶ D ′ ( Ω ) 0 φ ∈ D ( Ω ) p → ∞ lim ⟨ u p , φ ⟩ = 0.
我们通常说一个分布可以和一个 (有紧支集的) 光滑函数配对得到一个数, 即
D ′ ( Ω ) × D ( Ω ) → C , ( u , φ ) ↦ ⟨ u , φ ⟩ . 任意给定分布 u ∈ D ′ ( Ω ) D ( Ω ) 连续 线性泛函. 我们没有详细讨论和分布有关的拓扑线性空间的理论, 所以我们不打算对这一点做太多的展开 (这对于理解分布理论也没有影响) . 所谓的连续性, 可以用下面的序列的语言来描述: 对任意的试验函数序列 φ p ⟶ D 0 p → ∞ lim ⟨ u , φ p ⟩ = 0.
作为例子, 我们先学习一些重要的分布:
对任意的 a ∈ Ω δ a ∈ D ′ ( Ω ) φ ∈ D ( Ω ) ⟨ δ a , φ ⟩ = φ ( a ) . δ a
对任意的紧集 K ⊂ Ω a ∈ / K φ ∈ C K ∞ ( Ω ) ⟨ δ a , φ ⟩ = 0. a ∈ K φ ∈ C K ∞ ( Ω ) ∣ ∣ ⟨ δ a , φ ⟩ ∣ ∣ = ∣ ∣ φ ( a ) ∣ ∣ ⩽ 1 ⋅ ∣ α ∣ ⩽ 0 sup ∥ ∂ α φ ∥ L ∞ ( K ) . q = 0 C = 1
特别地, 我们还知道 δ a 0
给定开集 Ω f K ⊂ Ω f ⋅ 1 K ∈ L 1 ( Ω ) L loc 1 ( Ω ) Ω
对于任意的 f ∈ L loc 1 ( Ω ) D ( Ω ) T f : D ( Ω ) → C , φ ↦ ⟨ T f , φ ⟩ = ∫ Ω f ( x ) φ ( x ) d x . φ K T f Ω 0 K ⊂ Ω φ ∈ C K ∞ ( Ω ) ∣ ∣ ⟨ T f , φ ⟩ ∣ ∣ = ∣ ∣ ∫ K f ( x ) φ ( x ) d x ∣ ∣ ⩽ ∥ f ∥ L 1 ( K ) ∥ φ ∥ L ∞ ( K ) . q = 0 C = ∥ f ∥ L 1 ( K )
为了方便起见, 我们通常把 ⟨ T f , φ ⟩ ⟨ f , φ ⟩
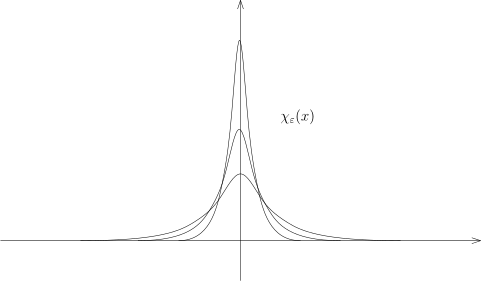
任意选定 χ ( x ) ∈ D ( R n ) χ ( x ) ∫ R n χ ( x ) d x = 1. ε > 0 χ ε ( x ) = ε n 1 χ ( ε x ) . ε → 0 χ ε ⟶ D ′ δ 0
由于 χ ε ∫ χ ε ( x ) φ ( x ) d x χ ε
证明. 通过换元积分公式, 我们知道对任意的
ε > 0 , 我们都有
∫ R n χ ε ( x ) d x = ∫ R n χ ( x ) d x , ∫ R n ∣ χ ε ( x ) ∣ d x = ∫ R n ∣ χ ( x ) ∣ d x . 任意选定试验函数
φ , 我们要证明
ε → 0 lim ⟨ χ ε − δ 0 , φ ⟩ = 0. 利用
∫ R n χ ε ( x ) d x = 1 , 我们有
⟨ χ ε − δ 0 , φ ⟩ = ∫ R n χ ε ( x ) φ ( x ) d x − φ ( 0 ) = ∫ R n χ ε ( x ) ( φ ( x ) − φ ( 0 )) d x = I 1 ∫ ∣ x ∣ ⩽ δ χ ε ( x ) ( φ ( x ) − φ ( 0 )) d x + I 2 ∫ ∣ x ∣ ⩾ δ χ ε ( x ) ( φ ( x ) − φ ( 0 )) d x 对于
I 1 而言, 当
ε → 0 时,
φ ( x ) 一致收敛到
φ ( 0 ) (因为
∣ x ∣ ⩽ ε ) , 所以, 我们有
∣ I 1 ∣ ⩽ o ( 1 ) ∫ ∣ x ∣ ⩽ δ ∣ χ ε ( x ) ∣ d x = o ( 1 ) ∥ χ ∥ L 1 . 其中
o ( 1 ) 是满足
lim δ → 0 o ( 1 ) = 0 的量.
所以, 可以先选
δ , 使得
∣ I 1 ∣ ⩽ ϵ , 其中,
ϵ 是任意给定的正实数. 对于
I 2 , 现在已经固定了
δ , 我们有
∣ I 2 ∣ ⩽ 2∥ φ ∥ L ∞ ∫ ∣ x ∣ ⩾ δ ∣ χ ε ( x ) ∣ d x = 2∥ φ ∥ L ∞ ∫ ∣ x ∣ ⩾ ε δ ∣ χ ( x ) ∣ d x = 2∥ φ ∥ L ∞ ∫ R n ∣ χ ( x ) ∣ 1 ∣ x ∣ ⩾ ε δ d x . 由于当
ε → 0 时,
∣ χ ( x ) ∣ 1 ∣ x ∣ ⩾ ε δ 是逐点收敛到
0 的, 所以, 根据 Lebesgue 控制收敛定理,
ε → 0 lim I 2 = 0. 特别地, 对足够小的
ε > 0 , 我们就有
∣ I 2 ∣ ⩽ ϵ . 这表明,
∣ I 1 + I 2 ∣ ⩽ 2 ϵ . 从而命题成立.
假设 μ ( Ω , B ( Ω )) Ω ⊂ R n B ( Ω ) σ K ⊂ Ω μ ( K ) < ∞
比如说, 对任意的正函数 (几乎处处) f ∈ L loc 1 ( Ω ) B ∈ B ( Ω ) μ f ( B ) = ∫ Ω 1 B ⋅ f ( x ) d x .
任意给定一个 Radon 测度 μ T μ φ ∈ D ( Ω ) ⟨ T μ , φ ⟩ = ∫ Ω φ ( x ) d μ ( x ) . T μ Ω 0
对任意的紧集 K ⊂ Ω φ ∈ C K ∞ ( Ω ) ∣ ∣ ⟨ T μ , φ ⟩ ∣ ∣ = ∣ ∣ ∫ K φ ( x ) d μ ( x ) ∣ ∣ ⩽ μ ( K ) ∥ φ ∥ L ∞ ( K ) . q = 0 C = μ ( K )
特别地, 我们可以把 L loc 1 ( Ω )
利用所谓的 Riesz 表示定理, 我们可以证明, Ω 0
我们自然还有阶非零的分布, 比如说, 我们可以定义 D ( R ) 上的线性泛函: ⟨ δ ′ , φ ⟩ = − φ ′ ( 0 ) , ⟨ u , φ ⟩ = k = 0 ∑ ∞ φ ( k ) ( k ) . 1
给定开集 Ω ⊂ R n T : L loc 1 ( Ω ) → D ′ ( Ω ) , f ↦ T f .
根据这个命题, 局部可积的函数可以看做是分布的子集合. 在分析中, 我们把 L loc 1 ( Ω ) Ω
证明. 假设 T f = D ′ 0 φ ∈ D ( Ω ) ∫ Ω f ( x ) φ ( x ) d x = 0 , f = 0 K ⊂ Ω f ∣ ∣ K = 0
我们定义函数
φ K ( x ) = { ∣ f ( x ) ∣ f ( x ) 1 K ( x ) , 0 , 如果 f ( x ) = 0 ; 如果 f ( x ) = 0. 这是一个有紧支集
K 的函数. 当
ε 较小时,
χ ε ∗ φ K 的支集仍然在
Ω 中: 按照卷积的定义, 对任意的
x ∈ supp ( χ ε ∗ φ K ) , 这个点距离
K 的不超过
ε , 然而, 距离
K 的不超过
ε 点是在
Ω 中的 (利用紧性) . 特别地, 我们得到一个试验函数
χ ε ∗ φ K ∈ D ( Ω ) , 从而
⟨ T f , χ ε ∗ φ K ⟩ = 0. 我们令
ε < δ 并且要求距离
K 的不超过
ε 点都落在
Ω 中. 我们令
K + B ( δ ) = { x + y ∣ ∣ x ∈ K , ∣ y ∣ ⩽ δ } . 根据定义, 我们就有
0 = ∫ Ω f ( x ) ( χ ε ∗ φ K ) ( x ) d x = ∫ R n f ( x ) ( χ ε ∗ φ K ) ( x ) d x = ∫ R n ( f ⋅ 1 K + B ( δ ) ) ( χ ε ∗ φ K ) d x = Fubini ∫ ∫ R n × R n ( f ( x ) 1 K + B ( δ ) ( x ) ) χ ε ( x − y ) φ K ( y ) d x d y = Fubini ∫ R n ( ∫ R n ( f ( x ) 1 K + B ( δ ) ( x ) ) χ ε ( x − y ) d x ) φ K ( y ) d y = ∫ R n ( ( f 1 K + B ( δ ) ) ∗ χ ε ) ( y ) φ K ( y ) d y . 然而, 我们上个学期证明过
( f 1 K + B ( δ ) ) ∗ χ ε ⟶ L 1 f 1 K + B ( δ ) , 从而 (由于
φ K ( y ) 有界) 当
ε → 0 , 我们有
0 = ε → 0 lim ⟨ T f , χ ε ∗ φ K ⟩ = ∫ R n ( f 1 K + B ( δ ) ) ( y ) φ K ( y ) d y = ∫ K ∣ f ( y ) ∣ d y . 所以对几乎处处的
x ∈ K , 我们有
f ( x ) = 0 , 命题得证.
我们注意到x 1 ∈ / L loc 1 ( R ) . 0 x − 1 n ⩾ 1 x 1 1 ∣ x ∣ ⩾ n 1 ( x ) ∈ L loc 1 ( R ) . ⟨ x 1 1 ∣ x ∣ ⩾ n 1 , φ ⟩ = ∫ − ∞ n 1 x φ ( x ) d x + ∫ n 1 ∞ x φ ( x ) d x = ∫ n 1 ∞ x φ ( x ) − φ ( − x ) d x . φ R
我们现在有个简单但是重要的观察: [ φ ( x ) − φ ( − x )] ∣ ∣ x = 0 = 0.
假设 ψ ( x ) ∈ C ∞ ( R ) ψ ( 0 ) = 0 x ψ ( x )
得到
x φ ( x ) − φ ( − x ) 是光滑函数 (自然是局部可积的) . 从而, 当
n → ∞ 时, 上述积分的极限存在:
n → ∞ lim ∫ n 1 ∞ x φ ( x ) − φ ( − x ) d x = ∫ 0 ∞ x φ ( x ) − φ ( − x ) d x . 我们现在定义
⟨ vp x 1 , φ ⟩ = ∫ 0 ∞ x φ ( x ) − φ ( − x ) d x . 为了证明这是分布, 我们利用中值定理: 对任意的紧集
K = [ − M , M ] ⊂ R , 对任意的支集在
K 上的光滑函数
φ , 我们有
∣ φ ( x ) − φ ( − x ) ∣ = ∣2 x φ ′ ( ξ ) ∣ ⩽ 2∥ φ ′ ∥ L ∞ ( K ) x . 所以,
∣ ⟨ vp x 1 , φ ⟩ ∣ ⩽ ∫ 0 M 2∥ φ ′ ∥ L ∞ ( K ) d x = 2 M ∥ φ ′ ∥ L ∞ ( K ) . 所以
vp x 1 是一个阶不超过
1 的分布. 在作业中, 我们将证明
vp x 1 的阶恰好是
1 .
另外, vp pv x 1