用户: ZhangYH/Lie 括号的差分直观

[差分] 可能在这里可能不是最合适的词, 我在这里用它主要是想表达 [通过看的见的量来理解看不见的极限] 这个意思. Lie 括号测量的是两个向量场的可交换程度, 在欧氏空间中我们可以让这句话有个定量的表达, 其中函数的 Taylor 展开起了很大作用. [差分] 也给了一个 Lie 括号就是 Lie 导数的一个非常直观的证明.

Lie 括号也很适合作为张量的分量计算的练习. 从微分流形的角度, 为什么 [差分] 定义的 Lie 括号是一个向量场, 能不能用直观的方式说明在坐标变换下 Lie 括号符合向量的规则? 这也是有意思的问题. Lie 括号有很多不同的抽象定义, 我们可以看到如何把具体的构造跟抽象的概念联系起来. 我们也可以比较 Lie 括号的各种不同定义, 找到不平凡的地方. 我觉得在映射不可逆时, Lie 括号的自然性就是一个比较不平凡的东西.

这里很多定义和证明都参考了 Lee 的 [光滑流形导论].

1Lie 括号的差分定义

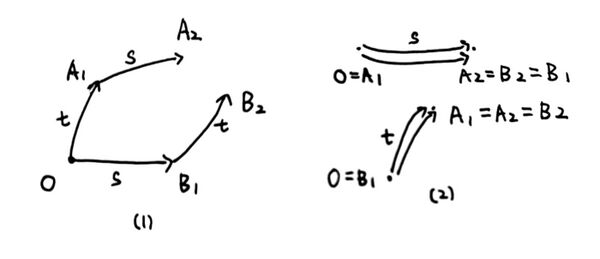
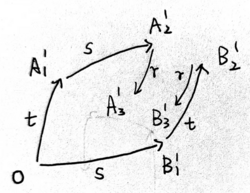
设 $X,Y$ 是 ${\mathbb{R}}^n$ 上的两个向量场. 考虑它们的积分曲线. (下图中是沿 $X$ 积分 $t$ 时间, 沿 $Y$ 积分 $s$ 时间.)

$v(x)=v(s,t):=\overrightarrow{B_2{A}_2}.$ 下面我们考虑 $v$ 关于 $s,t$ 的 Taylor 展开:$$v(s,t)=c_{s}s+c_{t}t+c_{ss}{s}^2+c_{tt}{t}^2+c_{ts}st+O(|x{|}^3).$$

注意到 $v(0,t)=v(s,0)\equiv 0$, 知 $c_s=c_t=c_{ss}=c_{tt}=0$, 故$$v(s,t)=c_{st}st+O(|x{|}^3).$$

我们称 $[X,Y]{|}_{p=0}:=c_{st}={\partial }_{st}v$ 为 $X,Y$ 在 $0$ 处的 Lie 括号. 很显然 $[X,Y]=-[Y,X]$.

2坐标表示, 等价的线段差分, 证明定义跟坐标无关

下面求 ${\partial }_{st}{A}_2$. 首先注意到 ${\partial }_s{A}_2=Y{|}_{A_1}$. 再对 $t$ 求导便有 ${\partial }_{st}{A}_2={\partial }_{X}Y$. 于是

$$[X,Y]={\partial }_{st}{A}_2-{\partial }_{st}{B}_2={\partial }_{X}Y-{\partial }_{Y}X=x^j{\partial }_j{y}^i-y^j{\partial }_j{x}^i.$$

如果在上面先对 $t$ 求导再对 $s$ 求导会怎样? 当然最终我们会得到一样的结论. 但是先对 $t$ 求导的话, 需要用到 ODE 关于初值的可微依赖性, 推导会更加的复杂.

观察上面的求导, 容易知道如果上面定义中的积分曲线换成相应的向量数乘得到的线段, 由此得到的 $\overrightarrow{B_2^{\prime }{A}_2^{\prime }}$ 跟原来的 $\overrightarrow{B_2{A}_2}$ 具有相同的 2 阶 Taylor 展开, 因此也可以表示 Lie 括号. (但是进一步推广应该就不行了, 这个时候不能保证只有 $c_{st}$ 非 $0$, 不过我还没有仔细验证过, 比如: 将积分曲线和线段混合起来. 第一条积分曲线可以换成端点处切向量相同的其它曲线.)

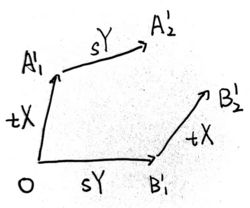
下面考虑坐标变换, 设基变换矩阵 (用复合求导, 不用死记) 为 $A={\tilde{\partial }}_i{\varphi }^j$, 它的逆矩阵为 $B={\partial }_i{\psi }^j$. 变换后的坐标为

$$\begin{array}{rl}[X,Y{]}^i& =b_k^j{x}^k{a}_j^l{\partial }_l(b_m^i{y}^m)-b_k^j{y}^k{a}_j^l{\partial }_l(b_m^i{x}^m)\\ & =x^l{\partial }_l(b_m^i{y}^m)-y^l{\partial }_l(b_m^i{x}^m)\\ & =b_m^i(x^l{\partial }_l{y}^m-y^l{\partial }_l{x}^m)+{\partial }_l{\partial }_m{\psi }^i(x^l{y}^m-x^m{y}^l)\\ & =b_m^i(x^l{\partial }_l{y}^m-y^l{\partial }_l{x}^m).\end{array}$$

符合 $1$-反变张量的变换规则, 因此 $[X,Y]$ 定义了一个向量场. 特别的对抽象的流形, 任意选取坐标表示, 可以按照第 1 节的差商来定义 Lie 括号.

3另外两种检验交换性的差分, 等价性

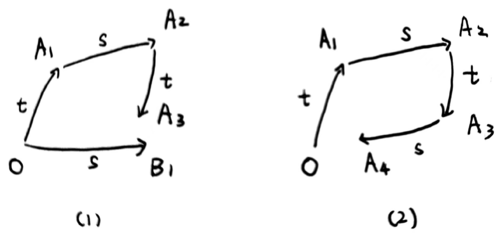
要利用积分曲线衡量两个向量场的交换性的话, 除了开头给出的差分, 还有其它两种差分表示, 如下图所示.

类似第 1 节中的推导, 可知上面两种差分得到的 $\overrightarrow{B_1{A}_3}$ 和 $\overrightarrow{O{A}_4}$ 的 2 阶 Tayler 系数中也只有 $c_{st}$ 项非 $0$. 下面我们证明三种差分的 $c_{st}$ 都是相等的.

我们先考虑 (2) 中的差分, 为了方便我们将耦合的变量分离开, 如下图所示.

注意到 ${\partial }_m{A}_4^{\prime }=Y{|}_{A_3^{\prime }}$, 故 ${\partial }_{rm}{A}_4^{\prime }=-{\partial }_{X}Y$. 要求出 ${\partial }_{tm}{A}_4^{\prime }$ 的一般形式的话不太方便, 但幸运的是我们只需知道它在 $0$ 处的取值, 因此在 $s=r=0$ 时对 $t$ 求导, 可知 ${\partial }_{tm}{A}_4^{\prime }{|}_0={\partial }_{X}Y{|}_0$.

类似的可以求出, 在 $0$ 处 ${\partial }_{sr}{A}_4^{\prime }=-{\partial }_{Y}X$, ${\partial }_{ts}{A}_4^{\prime }={\partial }_{X}Y$. 因此$${\partial }_{st}{A}_4=({\partial }_{rm}+{\partial }_{tm}+{\partial }_{sr}+{\partial }_{ts})A_4^{\prime }={\partial }_{X}Y-{\partial }_{Y}X.$$

下面考虑 (1) 中的差分, 我们用另外一种方法. 增加一个变量 $r$ 使得能从开头的差分过渡到 (1) 中的差分.

考虑 $u(x)=u(s,t,r):=\overrightarrow{B_3^{\prime }{A}_3^{\prime }}$ 的 Tayler 展开:

$$u(s,t,r)=c_{s}s+c_{t}t+c_{r}r+c_{ss}{s}^2+c_{tt}{t}^2+c_{rr}{r}^2+c_{ts}st+c_{tr}tr+c_{sr}sr+O(|x{|}^3).$$

注意到 $u(s,0,r)=u(0,r,t)\equiv 0$, 知上面的系数中也只有 $c_{st}={\partial }_{st}u{|}_0$ 可能非 $0$. 又注意到 $v(s,t):=\overrightarrow{B_1{A}_3}=u(s,t,t)$, 便知在 $0$ 处$${\partial }_{st}v={\partial }_{st}u+{\partial }_{sr}u={\partial }_{st}u=[X,Y].$$

4后两种差商的抽象定义, Lie 导数

在第 2 节中我们通过计算分量的坐标变换, 证明了 Lie 括号可以定义微分流形上的向量场. 我们能不能不利用具体的坐标, 纯粹利用抽象的流形概念来定义两个向量场的 Lie 括号呢?

事实上, 我们之前得到的三种差商都能找到抽象的表示方式. 我们先考虑第 3 节我们得到的两种差商.

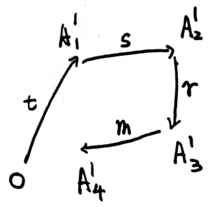
下面我们给出 (1) 的抽象表示. 考虑 ${\sigma }_t(s):=A_3(s,t)$, 它是一条光滑曲线. 它在 $0$ 处的切向量为 $D{\sigma }_t{|}_{s=0}$. 事实上 $\tau (t)=D{\sigma }_t{|}_{s=0}$ 是 $\mathbb{R}$ 到 $T_{0}M$ 的光滑映射, 可以再次对 $t$ 求导, 很容易能看出

$${\tau }^{\prime }(0)={\partial }_{ts}{A}_3={\partial }_{ts}(A_3-B_1)=[X,Y].$$

注意到 ${\tau }^{\prime }(0)\in T_{0}M$ 的定义只用到了流形的抽象概念, 我们实际上给出了 Lie 括号定义了流形上向量场的一个抽象证明. 我们将这样定义的 ${\tau }^{\prime }(0)$ 称为 $Y$ 沿着 $X$ 的 Lie 导数, 记为 ${\mathcal{L}}_{X}Y$, 显然 ${\mathcal{L}}_{X}Y=[X,Y]$.

如果把向量场 $Y$ 生成的流记作 $({\varphi }^t)$ 的话, 其实有 $\tau (t)=({\varphi }_{\ast }^t{)}^{-1}X{|}_{\varphi (p)}$. 从这里可以看到一个比较有意思的地方: 如果 $X$ 是一个在邻域之内有定义的向量场的话, 我们只需要 $Y$ 在沿着 $X$ 的一条积分曲线上有意义就足够定义 ${\mathcal{L}}_{X}Y$ 了, 这个时候之前得到的坐标公式也是有意义的.

有一个特例值得注意: 如果 $X\equiv {\partial }_1$, 那么 ${\mathcal{L}}_{X}Y={\partial }_{1}Y$. 这个结合 Flow Box 定理应该可以帮助理解的.

Lie 导数可以推广到张量上去. 我觉得 Lie 导数比较擅长处理由局部到整体的事情. 比如 $[X,Y]\equiv 0$ 可推出 $X,Y$ 可交换, 这个可以用 Lie 导数和 ODE 解的性质来做. 有时间可以写一写.

我们再给出 (2) 的抽象表示. 由差分的 Taylor 展开我们知道 $\sigma (t):=A_4(\sqrt{t},\sqrt{t})$ 是一条 $C^1$ 曲线 (不知道能否有更高的正则性), 它的切向量 $D\sigma {|}_{t=0}={\partial }_{st}{A}_4=[X,Y]$. $D\sigma {|}_{t=0}$ 的定义也只用到了抽象的流形概念.

5最开头差商的抽象表示

现在我们给出如何抽象的表示第 1 节的差分.

任意给定 $f\in C^{\infty }(M)$, 考虑$$\begin{array}{rl}{\Delta }_{1}f(s,t)& :=\frac{1}{st}[(f(A_2)-f(A_1))-(f(B_1)-f(O))],\\ {\Delta }_{2}f(s,t)& :=\frac{1}{st}[(f(B_2)-f(B_1))-(f(A_1)-f(O))].\end{array}$$

我们考虑 ${\Delta }_{1}f$ 的极限, 先令 $s\to 0$, 有

$$\underset{s\to 0}{\lim }{\Delta }_{1}f=\frac{1}{t}(Yf{|}_{A_1}-Yf{|}_O).$$

再令 $t\to 0$, 便得到了 ${\lim }_{s,t\to 0}{\Delta }_{1}f=XYf$. 因此

$$\underset{s,t\to 0}{\lim }({\Delta }_1-{\Delta }_2)f=(XY-YX)f.$$

我们想要说明 $(XY-YX)f=[X,Y]f$, 为此我们先注意到 $({\Delta }_1-{\Delta }_2)f=\frac{1}{st}(f(A_2)-f(B_2))$. 同时根据第 1 节的 Taylor 展开, 知 $\overrightarrow{B_2{A}_2}=[X,Y]st+O(|x{|}^3).$ 只需要再利用 $f$ 的 Taylor 展开便可得到结论:

$$f(A_2)-f(B_2)=(\overrightarrow{B_2{A}_2}\cdot \nabla )f+O(1)|\overrightarrow{B_2{A}_2}{|}^2=ts[X,Y]f+O(|x{|}^3).$$

这里 $(XY-YX)f$ 的定义同样也只用到了抽象流形的概念. 这里的证明方式可以跟数学分析中如何证明 $C^1$ 函数偏导数可交换的相比较.

变换 $G(f):=(XY-YX)f$ 为什么定义了一个切向量呢? 上面是通过差商直接给的证明, 我们也可以通过坐标计算来证明 $G(f)=[X,Y]f$.

$$\begin{array}{rl}{x}^i{\partial }_i(y^j{\partial }_j)-y^i{\partial }_i(x^j{\partial }_j)& =x^i{\partial }_i{y}^j{\partial }_j+x^i{y}^j{\partial }_{ij}-y^i{\partial }_i{x}^j{\partial }_j-y^i{x}^j{\partial }_{ij}\\ & =x^i{\partial }_i{y}^j{\partial }_j-y^i{\partial }_i{x}^j{\partial }_j.\end{array}$$

但其实也可以给一个抽象的证明. 注意到

$$XY(gf)=X[(Yg)f+g(Yf)]=(XYg)f+g(XYf)+(Yg)(Xf)+(Xg)(Yf).$$

直接计算知 $G(gf)=XY(gf)-YX(gf)=G(g)f+gG(f)$, 利用流形的知识可得 $G$ 确实是切向量.

为什么抽象的定义的 Lie 导数跟抽象定义的 Lie 括号相等呢? 上面利用差分给了一个证明. 其它的证明可以参考 Lee 的 [光滑流形导论], 也可以看看这个 MSE 的问题: https://math.stackexchange.com/questions/128195. 这些证明我还没有看完, 我也还不知道如何评价这些证明. 但是其中部分证明的思路跟这里的差分证明是相似的.

如果在某一点 $p$ 上 $X$ 和 $Y$ 都是 $0$, 这个时候 $[X,Y]$ 也只能是 $0$. 不管用坐标表示, 还是用这一节的抽象定义都比较容易证明这点. 然而, 用 Lie 导数的抽象定义其实也是可以证的, 此时 ${\varphi }^t(p)\equiv p$.

6Lie 括号和 Lie 导数的自然性

设 $X,Y$ 是 $M$ 上的向量场, $\tilde{X},\tilde{Y}$ 是 $N$ 上的向量场, $F$ 是 $M$ 到 $N$ 的光滑映射. 假设 $X,\tilde{X}$ 是 $F$-相关的, $Y,\tilde{Y}$ 是 $F$-相关的. 我们想证明 $[X,Y],[\tilde{X},\tilde{Y}]$ 也是 $F$-相关的.

如果 $F$ 是局部微分同胚, 我们可以利用坐标表示给一个证明. 具体计算跟第 2 节基变换的计算完全一样 (不知道能不能给个抽象的说法). 但是如果 $F$ 不可逆的话, 好像就不能用这样的方法了.

但是利用第 5 节得到的抽象定义, 我们却能给出一个很简单的证明.

$$\begin{array}{r}XY(f\circ F)=X((\tilde{Y}f)\circ F)=(\tilde{X}\tilde{Y}f)\circ F.\end{array}$$

因此 $[X,Y](f\circ F)=([\tilde{X},\tilde{Y}]f)\circ F$, 完成了证明.

上面的证明也可以写成坐标形式, 即任意给定 $\tilde{g}\in C^{\infty }(N)$, 有$$x^i{\partial }_i(y^j{\partial }_j\tilde{g})=x^i{\partial }_i(y^j{\partial }_j{F}^k{\tilde{\partial }}_k\tilde{g})=x^i{\partial }_i({\tilde{y}}^j{\tilde{\partial }}_k\tilde{g})=x^i{\partial }_i{F}^m{\tilde{\partial }}_m({\tilde{y}}^j{\tilde{\partial }}_k\tilde{g})={\tilde{x}}^m{\tilde{\partial }}_m({\tilde{y}}^j{\tilde{\partial }}_k\tilde{g}).$$我感觉做这种涉及两个流形之间映射的张量计算时, 还是不要不动脑子, 还是需要搞清楚这些坐标代表着什么.

除了 $XY-YX$ 的抽象定义, 我们知道 Lie 括号还有一个抽象定义, 就是第 4 节给的 [Lie 导数]. 类似的, 我们也可以考虑能不能从 Lie 导数的角度去证明自然性, 我本来以为做不到, 但其实可以给一个证明, 这个证明也可以推广到反变张量的 Lie 导数上面去:

设 $X$ 生成的流为 $\varphi (t,p)={\varphi }^t(p)$, $\tilde{X}$ 生成的流为 $\psi (t,p)={\psi }^t(p)$. 注意到 $\psi (\cdot ,F(p))$ 和 $F\circ \varphi (\cdot ,p)$ 都是从 $F(p)$ 出发的关于 $Y$ 的积分曲线. 由唯一性知 $F\circ {\varphi }^t={\psi }^t\circ F$, 因此 $d{F}_{{\varphi }^t(p)}{\varphi }_{\ast }^t={\psi }_{\ast }^{t}d{F}_p$, 故 $({\psi }_{\ast }^t{)}^{-1}d{F}_{{\varphi }^t(p)}=d{F}_p({\varphi }_{\ast }^t{)}^{-1}$. 于是

$$d{F}_p{\mathcal{L}}_{X}Y=\frac{d}{dt}d{F}_p({\varphi }_{\ast }^t{)}^{-1}{Y}_{{\varphi }^t(p)}=\frac{d}{dt}({\psi }_{\ast }^t{)}^{-1}d{F}_{{\varphi }^t(p)}{Y}_{{\varphi }^t(p)}=\frac{d}{dt}({\psi }_{\ast }^t{)}^{-1}{\tilde{Y}}_{{\psi }^t(F(p))}={\mathcal{L}}_{\tilde{X}}\tilde{Y}.$$

我也在 MO 上问了一个相关的问题: https://mathoverflow.net/questions/467911. 这个问题下有个答案利用 $TTM$ 给出了 Lie 括号的另一种抽象定义. 其实考虑积分曲线的唯一性的话, 我们也可以用之前的差分定义, 通过 Taylor 展开得到一个 Lie 括号自然性的证明.

如果 $F$-相关的条件只在某一点 $p$ 满足, 而不是在一个邻域满足的话, 是没有类似的结论的. 在 $\mathbb{R}$ 上就能构造反例.

7加法和数乘, Jacobi 恒等式

首先我们证明 $[X,Y+Z]=[X,Y]+[X,Z]$. 这个关系不管是用坐标表示, 还是用 Lie 括号和 Lie 导数的抽象定义都是非常直接的.

接下来我们证明 $[X,gY]=f[X,Y]+(Xg)Y$. 这个关系从 Lie 导数的抽象定义 (第 4 节) 可能是比较直观的. 使用 Lie 括号的抽象定义 (第 5 节) 的话, 可以有以下证明:

$$[X,gY]=X(gY)-gYX=(Xg)Y+gXY-gYX=(Xg)Y+g[X,Y].$$

而利用坐标表示的话, 证明如下

$$x^i{\partial }_i(g{y}^j)-g{y}^i{\partial }_i{x}^j=x^i{\partial }_{i}g{y}^j+g(x^i{\partial }_i{y}^j-y^i{\partial }_i{x}^j).$$

最后我们来考虑 Jacobi 恒等式, 即 $[X,[Y,Z]]=[[X,Y],Z]+[Y,[X,Z]]$. 关于怎么去理解 Jacobi 恒等式, 我觉得这个 MSE 问题说的比较清楚: https://math.stackexchange.com/questions/113766. 用 Lie 括号的抽象定义, 可以把它转化成算子的交换子问题$$[X,Y]Z+Y[X,Z]=(XY-YX)Z+Y(XZ-ZX)=XYZ-YZX=[X,YZ].$$用 Lie 导数的抽象定义的话, 我觉得可能不会有自然的证明. 利用坐标表示也可以写出一个证明, 注意到

$$\begin{array}{rl}{\partial }_X[Y,Z]-{\partial }_{[Y,Z]}X& ={\partial }_X{\partial }_{Y}Z-{\partial }_X{\partial }_{Z}Y-{\partial }_{[Y,Z]}X,\\ {\partial }_Z[X,Y]-{\partial }_{[X,Y]}Z& ={\partial }_Z{\partial }_{X}Y-{\partial }_Z{\partial }_{Y}X-{\partial }_{[X,Y]}Z,\\ {\partial }_Y[Z,X]-{\partial }_{[Z,X]}Y& ={\partial }_Y{\partial }_{Z}X-{\partial }_Y{\partial }_{X}Z-{\partial }_{[Z,X]}Y.\end{array}$$

上面三式加起来为 $0$. 事实上这里还是要用到第 5 节中 Lie 括号是求导算子的交换子这一结论. 我也不知道怎么评价这个证明, 如果把分量表示写出来直接计算的话, 应该会非常麻烦, 所以第 5 节中的那个抽象表示确实很重要.