用户: Cybcat/Coxeter 群

Coxeter 群是什么捏? 别急, 让我们先讲讲数学史.

古早的人们喜欢研究正多边形和正多面体. 没错儿, 尽管那时候人们不知道群是什么玩意, 但是人们发现这些几何体对称而漂亮, 看着它们就能让人感到神圣. 这方面古希腊人已经玩的比较明白了.

当然, 从群论的角度看, 某种意义上可以认为, $O(2)$ 的有限子群很早就被世界各地的先贤们熟知, 就是二面体群 $D_n$ 以及循环群 $C_n$. 毕竟它们来自正多边形的对称性, 平面上具有强对称性的图形还是比较容易研究的. 那再来说 $O(3)$, 虽然说古希腊人确定的知道了正多面体就是那五个, 而且他们也明白对称的基本操作反射和旋转, 但是严格来说, 那时候还没有人研究空间中这些几何变换在复合下封闭的有限结构.

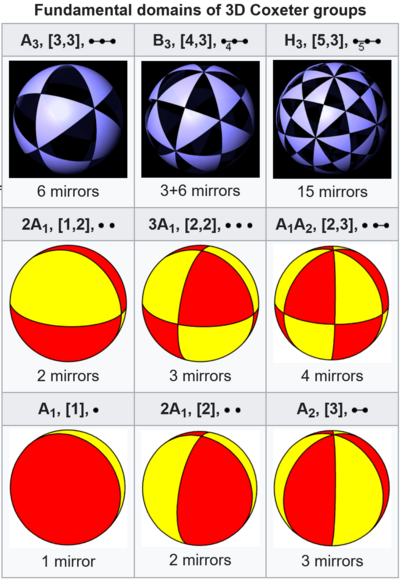
这就要到 1852 年, Möbius 分类了 $O(3)$ 中反射生成的有限子群, 通过它们按照等距同构作用在球面上, 他发现基本区域不白给, 其形状必然是一个球面三角形 (或者退化情况的 “两角形”, “一角形”, 退化情况像一瓣橘子, 球面角度数 $\frac{\pi }{p}$), 球面三角的三个球面角的度数分别为 $\frac{\pi }{p},\frac{\pi }{q},\frac{\pi }{r}$, 分母都是正整数. 而且由于在球面上, 内角和条件为 $\frac{1}{p}+\frac{1}{q}+\frac{1}{r}>1$, 还可以不妨设 $p\ge q\ge r\ge 2$. 这样一来所有情况只有 $(p,2,2),(3,3,2),(4,3,2),(5,3,2)$. 退化情况给出 $D_p$, $(p,2,2)$ 给出 $C_2\times D_p$, 后三者给出四面体群, 八面体群, 二十面体群 $S_4,C_2\times S_4,C_2\times A_5$.

这里还有更多解释, 基本区域占总球面面积的比例为 $4\pi /(\frac{\pi }{p}+\frac{\pi }{q}+\frac{\pi }{r}-\pi )$, 因为 $O(3)$ 的作用忠实, 所以这个值也给出群的阶数, 分别是 $4p,24,48,120$, 如下图的图所示. 我们知道 $\mathrm{SU}(2),\mathrm{SO}(3),\mathrm{O}(3)$ 的有限子群这些玩意都对应有一个 ADE 分类, 比如这三个 “例外的” 四面体, 八面体, 二十面体的情况对应了 ${\mathsf{E}}_6,{\mathsf{E}}_7,{\mathsf{E}}_8$, 然而在 Coxeter 群的体系中, 它们被叫做 Coxeter 系统 ${\mathsf{A}}_3,{\mathsf{B}}_3,{\mathsf{H}}_3$, 后面我们会解释这些记号对应的根系是什么意思.

此外, Riemann, Schwarz, Poincaré 和 Klein 还研究了 ${\mathbb{R}}^2,{\mathbb{H}}^2$ 上 (关于多边形的) 反射离散群.

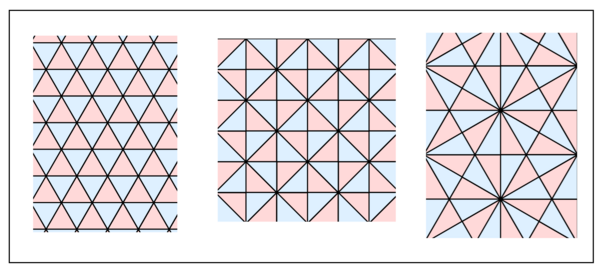
对于欧氏平面, 仍然是刚才的 $(p,q,r)$ 刻画, 我们要求刚好有 $\frac{1}{p}+\frac{1}{q}+\frac{1}{r}=1$, 此时对应的 $(p,q,r)=(3,3,3),(4,4,2),(6,3,2)$. 很明显, 它们和平面的多边形密铺有关: 分别是正三角形, 正方形, 正六边形的密铺. 这些美丽的构造显然在全世界从古到今的平面设计中被广泛地应用. 当然, 在 ADE 分类中, 这三个分别是仿射 (扩展)Dynkin 图 $\widetilde{{\mathsf{E}}_6},\widetilde{{\mathsf{E}}_7},\widetilde{{\mathsf{E}}_8}$. 在 Coxeter 群的体系中, 也有对应的, 它们是 $\widetilde{{\mathsf{A}}_2},\widetilde{{\mathsf{C}}_2},\widetilde{{\mathsf{G}}_2}$.

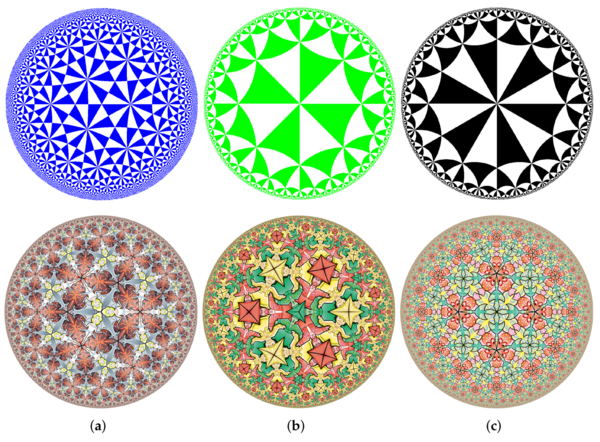
当然, 双曲平面 (Poincaré 圆盘模型或者上半平面模型) 也有类似的刻画, 比如下面的图片展示了著名艺术家 Escher 的作品和一些双曲的 $(p,q,r)$. 例如蓝绿黑的圆盘从左往右分别是 $(7,3,2),(4,4,4),(6,4,3)$. Escher 的作品从左往右则是 $(4,3,3),(4,4,3),(5,4,4)$. 愿意的话你也可以画出它们的 Dynkin 图, 但是可以预料的是, 到高维我们不再可以像前面这些情况一样有简单分类.

这些 $(p,q,r)$ 和 Schläfli 记号有关系, 不过 Schläfli 这哥们主要研究的是多边形密铺, 所以他首先定义记号 $\{p\}$ 表示一个正 $p$ 边形, 然后记号 $\{p,q\}$ 就表示有 $q$ 个正 $p$ 边形围绕着一个顶点. 不难发现, $\{p,q\}$ 和 $(p,q,2)$ 具有密切的关系, 它们就差一个 Barycentric subdivision(重 zhòng 心重 chóng 分). 也就是说对每个正多边形形状的面, 连接其中心和每条边的中点, 连接其中心和每个顶点, 得到的基本区域就是 $(p,q,2)$. 此时我们能看出 $\{p,q\}$ 和 $\{q,p\}$ 之间具有的微妙联系: 它们差一个顶点和面的对偶, 也就是说取每个面的中心作为顶点, 连接新的顶点和相邻最近的顶点, 得到的就是对偶的密铺.

Schläfli 将这种技术手段发扬光大, 以至于能研究 ${\mathbb{R}}^{n+1}$ 中的 “正多胞体”, 它们其实就是 ${\mathbb{S}}^n$ 的 “正多胞面” 密铺. 而巧合的是, 在 1890 年附近, Killing 和 Cartan 搞明白了复半单李代数的分类, 他们研究了这些李代数的根系, 是的, 它们都对应 Dynkin 图, 我们的老朋友. 然后 1925 年, Weyl 证明了这些根系的对称群, 也就是 Weyl 群, 是一个反射群.

然后这两条线终于走到了一起, 大约 1930 年左右, Coxeter 分类了 ${\mathbb{S}}^n,{\mathbb{R}}^n$ 的离散反射群. 这说明在 ${\mathbb{H}}^n$ 中因为负的曲率, 空间看起来更 “大” 了, 所以事情确实更加复杂.

不管那么多, 我们还是先从熟悉的例子入手, 我们回到 $S_4,C_2\times S_4,C_2\times A_5$ 这三个群. 它们有什么共同点呢? 对于一个内角 $\frac{\pi }{p},\frac{\pi }{q},\frac{\pi }{r}$ 的球面三角形, 我们可以考虑关于其三边的球面反射, $s_1,s_2,s_3$, 很明显它们都是 $O(3)$ 中的元素, 而且满足这样一些关系, $s_1^2=s_2^2=s_3^2=1$, 而且两次反射相当于一次旋转, 角度为 $\frac{2\pi }{p},\frac{2\pi }{q},\frac{2\pi }{r}$, 即 $s_1{s}_2,s_2{s}_3,s_3{s}_1$ 的阶为 $p,q,r$. 事实就是, 这些关系生成了整个群! 简单来说, 这是因为每个基本区域都可以由不断地反射生成得到! 因此我们考虑如下的群$$W:=⟨s_1,s_2,s_3:s_1^2=s_2^2=s_3^2=(s_1{s}_2{)}^4=(s_2{s}_3{)}^3=(s_3{s}_1{)}^2=1⟩,$$这个群的中心是 $C_2$, 生成元为 $c=s_3{s}_2{s}_1{s}_2{s}_3{s}_1{s}_2{s}_1{s}_2$. 剩下全体由偶数个 $s_i$ 乘起来的元素构成一个子群, 它同构于 $S_4$, 可以检查 $S_4\times C_2\cong W$ 就是整个群.

总的来说, 最后事情被提炼为如下的资料

定义 0.1 (Coxeter 系统). 设 $S$ 是一个字符集, 代表了反射的生成元. 定义 $m:S\times S\to {\mathbb{Z}}_{\ge 1}\cup \{\infty \}$, 其中 $m(s,s)=1$ 对一切 $s\in S$, $m(s,t)=m(t,s)\ge 2$ 对一切 $S$ 中的 $s\ne t$, 也可以等于无穷. 那么考虑这样一个群$$W=⟨s\in S:(st{)}^{m(s,t)}=1,\forall s,t\in S⟩,$$我们称 $(W,S)$ 为一个 Coxeter 系统, $W$ 为该系统的 Weyl 群.

这里 $(st{)}^m=1$ 当且仅当 $(ts{)}^m=1$.