用户: Cybcat/曲线模空间/JS第四讲

1第四讲

亏格 $0$ 光滑曲线

鉴于这是一个重要例子, 让我们做地仔细一些.

我们要研究的对象是 ${\mathcal{M}}_{0,n},{\overline{\mathcal{M}}}_{0,n}$. 鉴于先前所言, 需要 $n\ge 3$ 时这里的讨论才有意义, 因为我们总能将三个点变成 $0,1,\infty$. 先看光滑者, 就有 $C\cong {\mathbb{P}}^1$, 于是$$(C,p_1,p_2,p_3,\cdots ,p_n)\cong ({\mathbb{P}}^1,0,1,\infty ,p_4,\cdots ,p_n).$$你可能觉得已经差不多搞明白了, 但是先别急, 严谨的证明并没有你想象中的那般简单, 我们需要这样一个引理, 但是因为技术是纯代数几何的, 让我们在下一讲再补充其证明.

引理 1.1. 设 $\pi :C\to B$ 为光滑, 紧合, 满, 局部有限表现同态, 相对维数不超过 $1$, 几何纤维同构 ${\mathbb{P}}^1$.

(a) 若 $\pi$ 具有截面 $p_1:B\to C$. 则 $B$ 上存在一个秩 $2$ 向量丛 $\mathcal{E}$ 使得于 $B$ 上 $C\cong \mathbb{P}(\mathcal{E})$.

(b) 若 $\pi$ 具有两个不交截面 $p_1,p_2:B\to C$, 则 $\mathcal{E}\cong {\mathcal{L}}_1\oplus {\mathcal{L}}_2$ 为线丛直和.

(c) 若 $\pi$ 具有三个不交截面 $p_1,p_2,p_3:B\to C$, 则 $\mathcal{E}$ 可被选取为 ${\mathcal{O}}_B\oplus {\mathcal{O}}_B$, 由此 $C\cong B\times {\mathbb{P}}^1$.

命题 1.2. 簇 $M_{0,3}=\mathrm{Spec}\mathbb{C}$ 是一个点, 给出了 ${\mathcal{M}}_{0,3}$ 函子的精模空间, 且万有族为$$(\pi :{\mathbb{P}}^1\to \mathrm{Spec}\mathbb{C};p_1=0,p_2=1,p_3=\infty :\mathrm{Spec}\mathbb{C}\to {\mathbb{P}}^1).$$

证明. 记 $h=h^{\mathrm{Spec}(\mathbb{C})}$ 需证明 ${\mathcal{M}}_{0,3}$ 同构于它. 首先对 $\mathbb{C}$-概形 $S$, $h(S)=\{S\to \mathbb{C}\}$ 只有一个元素, 那么我们要将一般的光滑亏格 $0$ 曲线族$$(\pi :C\to S;p_1,p_2,p_3:S\to C)\in {\mathcal{M}}_{0,3}(S)$$典范同构到平凡族$$(\pi :S\times {\mathbb{P}}^1\to S;0,1,\infty :S\to S\times {\mathbb{P}}^1).$$注意到上面的平凡族是典范构造的, 自然有关于 $S$ 选取的函子性, 这足以证明 ${\mathcal{M}}_{0,3}\cong h$. 注意到 1.1 告诉我们 $C\cong S\times {\mathbb{P}}^1$, 因此这诱导了映射$$A=(p_1,p_2,p_3):S\to (({\mathbb{P}}^1{)}^3\backslash \Delta )\cong \mathrm{PGL}(2,\mathbb{C}).$$这里 $\Delta \subset ({\mathbb{P}}^1{)}^3$ 是大对角线, 包含任意两个分量相等者, 然后这同构于 $\mathrm{PGL}(2,\mathbb{C})$ 是因为三个互不相同的点 $p_1,p_2,p_3$ 的像到 $0,1,\infty$ 的 ${\mathbb{P}}^1$ 自同构是唯一确定的一个 $\mathrm{PGL}(2,\mathbb{C})$ 中的元素. 最后考虑自同构 $S\times {\mathbb{P}}^1\to S\times {\mathbb{P}}^1$ 自同构把 $p_1,p_2,p_3$ 映到 $0,1,\infty$ 的映射由$$S\times {\mathbb{P}}^1\to S\times {\mathbb{P}}^1,(s,p)\mapsto (s,A(s{)}^{-1}p)$$给出, 而一切事情在 $S\to T$ 的拉回下典范 (为什么), 所以 ${\mathcal{M}}_{0,3}\cong h$ 得到验证, 最后万有族的事实留给读者作为习题.

$\square$

一旦打开了潘多拉的魔盒, $n\ge 4$ 的情况就不再是问题. 对一般情况下我们仍然能用上面的方法自同构前三个点到达 $0,1,\infty$. 剩下 ${\mathbb{P}}^1$ 中这些点就帮我们唯一地决定了在 $(C;p_1,\cdots ,p_n)$ 中的同构类. 然后加之互不相同的条件, 我们实则得到

命题 1.3. 对 $n\ge 3$, 模函子 ${\mathcal{M}}_{0,n}$ 对应着精模空间$$M_{0,n}=({\mathbb{P}}^1\backslash \{0,1,\infty \}{)}^{n-3}\backslash \Delta .$$其中 $\Delta =\{(q_i{)}_i:\exists i\ne j,q_i=q_j\}$ 为大对角线. 对应的万有族为$$(\pi :M_{0,n}\times {\mathbb{P}}^1\to M_{0,n};p_1=0,p_2=1,p_3=\infty ,(p_4^{\prime },\cdots ,p_n^{\prime }):M_{0,n}\to M_{0,n}\times {\mathbb{P}}^1).$$

注 1.4. $n\ge 3$ 时, 首先 $M_{0,n}$ 不仅是精模空间, 而且它是正规 (甚至光滑的), 不可约, $n-3$ 维的 $\mathbb{C}$-代数簇.

另外我们也能看见 $M_{0,n}\subset {\overline{M}}_{0,n}^0$, 因为固定三个点后就不再有 ${\mathbb{P}}^1$ 的自同构.

尽管是亏格 $0$ 光滑的特殊情况, 但是必须得说我们已经有那么一点理解了. 下一节我们将引入研究不光滑, 稳定曲线的重要道具, 那就是对偶图.

对偶图的引入

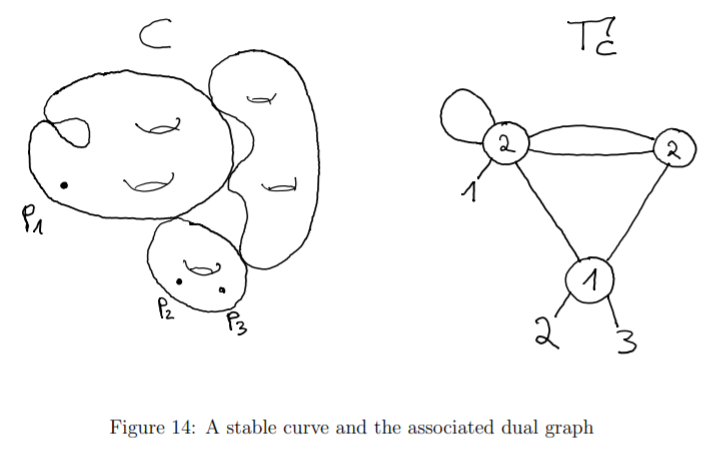
让我们先来思考一个问题, 怎么样抽象地记录一个稳定曲线的拓扑信息呢? 读者请先自己思考, 然后我们来玩一个小游戏: 请思考下面左右两侧的对象是怎么对应起来的:

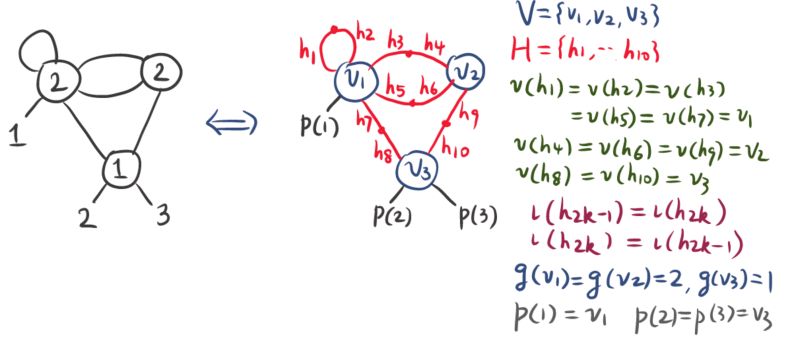
定义 1.5. 一个对偶图包含如下的资料: $$\Gamma :=(V,H,v:H\to V,\iota :H\to H,g:V\to {\mathbb{Z}}_{\ge 0},n,p:\{1,2,\cdots ,n\}\to V).$$

其中:

$\bullet$ $V$ 是顶点集. $V$ 是有限集.

$\bullet$ $H$ 是半边集, $H$ 是有限集.

$\bullet$ $v:H\to V$ 记录了半边如何连接到顶点上.

$\bullet$ $\iota :H\to H$ 是半边集的配对, 满足 ${\iota }^2={\mathrm{id}}_H$ 以及 $\iota (h)\ne h$ 对一切 $h\in H$.

$\bullet$ $g:V\to {\mathbb{Z}}_{\ge 0}$ 是一个从顶点集到自然数 ${\mathbb{Z}}_{\ge 0}$ 的映射, 对 $v\in V$, 称 $g(v)$ 为顶点 $v$ 的亏格.

$\bullet$ $n\in {\mathbb{Z}}_{\ge 0}$ 是一个非负整数, 称为标记点数.

$\bullet$ $p:[n]\to V$ 称为标记 (函数), $\{1,2,\cdots ,n\}$ 是标记点的编号, $p$ 将它们打到对应的顶点.

$\circ$ 此外对一个顶点 $v\in V$, 定义$$n(v):=\#\{h:v(h)=v\}+\#\{n:p(n)=n\}$$为 $v$ 连接的半边数加上标记数.

$\circ$ 顶点 $v\in V$ 的稳定性条件指 $2g(v)-2+n(v)>0$.

$\circ$ 对偶图 $\Gamma$ 对应的图 $G=(V,E)$, 具有相同的顶点集, 边集 $E$ 为 $H$ 的 $\iota$ 轨道, 将一个轨道中的两个 $h$ 对应的 $v(h)$ 相连. 所以 $E$ 中可以有重复的边, 也可以有自环.

$\circ$ 对偶图 $\Gamma$ 称为稳定的, 指它对应的图是连通的, 而且每个顶点都满足稳定性条件. 稳定的对偶图称为稳定图.

注 1.6. 这里我们要指出, 我们允许对偶图的定义更加一般, 纯粹是为了组合数学上的一般性, 因为这个组合对象没有比一个图多太多结构. 把这些关于稳定性的要求加入对偶图的定义中在某种意义上不大合理.

下面的图中, 我们展示了前文中的对偶图按定义给出的信息:

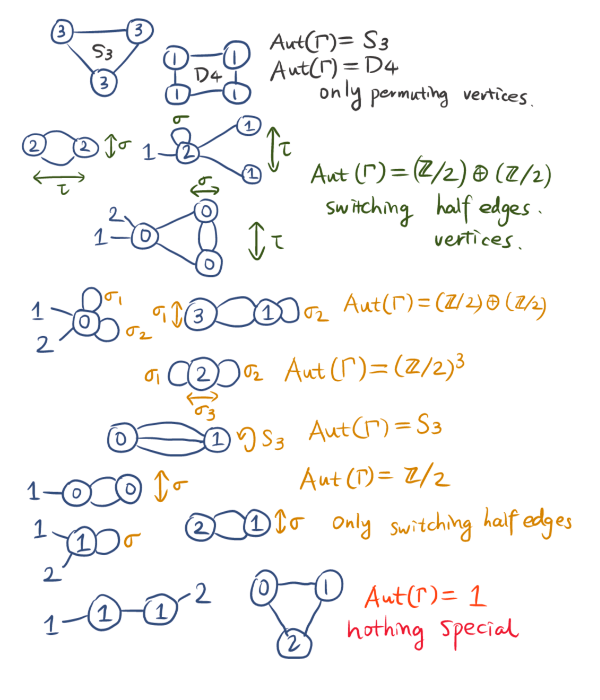
定义 1.7. 两个对偶图的同构$$\varphi :\Gamma =(V,H,v,\iota ,g,n,p)\to {\Gamma }^{\prime }=(V^{\prime },H^{\prime },v^{\prime },{\iota }^{\prime },g^{\prime },n^{\prime },p^{\prime })$$包含了如下资料:

$\bullet$ ${\varphi }_V:V\to V^{\prime },{\varphi }_H:H\to H^{\prime }$ 给出集合上的双射.

$\bullet$ 对 $v\in V,h\in H$, 我们有: $$v^{\prime }({\varphi }_H(h))={\varphi }_V(v(h)),{\varphi }_H(\iota (h))={\iota }^{\prime }({\varphi }_H(h)),g^{\prime }({\varphi }_G(v))=g(v).$$

$\bullet$ $n=n^{\prime }$.

$\bullet$ 对任意正整数 $1\le k\le n$, $p^{\prime }(k)={\varphi }_V(p(k))$.

换言之, 对应的 ${\varphi }_V,{\varphi }_H$ 具有一切需要的相容性. 容易证明, $\Gamma$ 的全体自同构形成一个群, 记为 $\mathrm{Aut}(\Gamma )$, 称 $\Gamma$ 的自同构群. 一些简单的自同构群例子如下:

定义 1.8. 定义对偶图 $\Gamma$ 的亏格 $g(\Gamma )$ 为$$g(\Gamma ):=1+\#E-\#V+\sum _{v\in V}g(v).\#E=\frac{1}{2}\#H.$$即 $\Gamma$ 作为图 $(V,E)$ 的图论亏格加上所有顶点的亏格, 因为本质上把顶点想象为有 $g(v)$ 亏格的闭曲面, 然后依照图的边构建这些对象的连通和, 这时候计算的亏格就是真切的作为拓扑对象的亏格.

另外对偶图 $\Gamma$ 的标记点数记 $n(\Gamma ):=n$.

现在我们终于可以对一个节点曲线 (稳定曲线) 定义其对应的对偶图 (稳定图):

定义 1.9. 一个稳定曲线 $(C;p_1,\cdots ,p_n)$ (更一般地, 对复射影节点曲线 $C$ 也能作此讨论, 其上允许添加有限个互不相同, 不在节点处的标记点 $p_1,\cdots ,p_n$) 的对偶图, 是其按照如下构建规则得到的对偶图:

$\bullet$ 顶点集 $V$ 取作正规化 $\tilde{C}$ 的连通分支 ${\tilde{C}}_v$.

$\bullet$ 半边集 $H$ 取作 $C$ 中节点在正规化 $\tilde{C}\to C$ 下的原像.

$\bullet$ 函数 $v$ 取作节点原像 $h\in H$ 所在的连通分支 ${\tilde{C}}_v$.

$\bullet$ 对合 $\iota$ 交换节点对应的原像对子 (注意一个节点恰好有两个原像).

$\bullet$ 亏格 $g(v):=g({\tilde{C}}_v)$.

$\bullet$ 标记点数 $n$ 就是稳定曲线的标记点数 $n$.

$\bullet$ 标记函数 $p$ 将正整数 $k$ 打到 $p_k$ 正规化原像所在的连通分支 ${\tilde{C}}_v$(注意标记点不能是节点恰好有一个原像).

对偶图有关的性质, 我们将在下一小节进行展示.

对偶图的基本性质

首先是一些最基本的概念:

命题 1.10. 关于曲线与对偶图最基本的概念对应:

(1) 一个复射影带标记节点曲线的算术亏格等于其对偶图的亏格.

(2) 一个复射影带标记节点曲线稳定当且仅当其对偶图稳定. 由此, 说法 " 稳定曲线的稳定图 " 是良定义的.

(3) 对复射影带标记节点曲线 $(C;p_1,\cdots ,p_n)$ 及对偶图 $\Gamma$, 有群正合列$$0\to \prod _{v\in V(\Gamma )}\mathrm{Aut}({\tilde{C}}_v,\text{其上全体特殊点(节点原像与标记点)})\to \mathrm{Aut}(C;p_1,\cdots ,p_n)\to \mathrm{Aut}(\Gamma ).$$

证明. (1) 与 (2) 留给读者. 对于 (3), $C$ 固定诸 $p_i$ 的自同构 $\sigma$ 诱导了对应对偶图的自同构 ${\sigma }^{\prime }$, 具体来说, $\sigma$ 诱导了 $\tilde{C}$ 连通分支间的对应关系, 给出了 ${\sigma }_V^{\prime }$; 而节点仍映射为节点, 节点对应两个 (可能为同一个) 连通分支也被 $\sigma$ 连带作用, 给出了 ${\sigma }_H^{\prime }$ 以及对应函数 $\iota$ 和 $v$ 的相容条件. 而且 $\sigma$ 不改变亏格, 也不改变标记点数和标记点所在的分支. 于是 ${\sigma }^{\prime }$ 良定义.

然后观察 ${\sigma }^{\prime }$ 平凡当且仅当 ${\sigma }_V^{\prime }$ 和 ${\sigma }_H^{\prime }$ 平凡, 换言之每个分支映射 ${\tilde{C}}_v$ 到自身, 不改变其上的标记点以及节点, 换言之该自同构来自每个 ${\tilde{C}}_v$ 上固定特殊点作自同构, 即来自正合列的第二项, 结论得证.

$\square$

注 1.11. 这里的正合列中最后的映射不见得总是满的, 例如可以两个不同构的椭圆曲线通过一个节点适当地粘起来, 稳定图上看无法区分这二者, 从而存在自同构交换它们, 但是这一自同构无法在黎曼面的层面实现.

另外尽管这里的命题 (1)(3) 都对节点曲线陈述, 但是一般使用时都只考虑稳定者.

然后是一些关于对偶图及稳定性本身的性质:

命题 1.12. (1) 对偶图的亏格和标记点数是各个连通分支对应者的和.

(2) 稳定图 $\Gamma$ 作为图的边数 $\#E$ 至多为 $3g(\Gamma )-3+n(\Gamma )$, 顶点数 $\#V$ 至多为 $2g(\Gamma )-2+n(\Gamma )$.

(3) 给定 $g,n\in {\mathbb{Z}}_{\ge 0}$, 存在有限多种 (同构意义下) 稳定图 $\Gamma$ 具有 $g(\Gamma )=g,n(\Gamma )=n$.

证明. (1) 显然. 对于 (2), 注意对每个顶点, 展开 $n(v)$ 后, 稳定的定义为$$2g(v)-2+v\text{的标记点数}+v\text{的度数}\ge 1,$$稍微变形一下然后对全体顶点求和即得到$$2\sum _{v}g(v)-3\#V(\Gamma )+n(\Gamma )+2\#E(\Gamma )\ge 0.$$这也就是$$2g(\Gamma )-2+n(\Gamma )\ge \#V(\Gamma ).$$注意到 $\sum g(v)\ge 0$, 于是把它也加一份到左边, 得到$$3g(\Gamma )-3+n(\Gamma )=3\sum _{v}g(v)+3+3\#E(\Gamma )-3\#V(\Gamma )+n(\Gamma )\ge \#E(\Gamma ).$$最后 (3) 则是 (2) 的立刻推论.

$\square$

这里 $3g-3+n$ 第一次出现, 以后我们将会看到它和维数间的密切联系. 另外, 其实亏格和标记点数给定后, 稳定图的可能性仍然非常多. 下面是一个表格, 记录了对于一些 $(g,n)$ 稳定图的数量:

$n$	$0$	$1$	$2$	$3$	$4$	$5$	$6$	$7$
$g=0$	$0$	$0$	$0$	$1$	$4$	$26$	$236$	$2752$
$g=1$	$0$	$2$	$5$	$23$	$163$	$1576$	$\cdots$
$g=2$	$7$	$16$	$75$	$555$	$5608$	$\cdots$
$g=3$	$42$	$181$	$1355$	$\cdots$
$g=4$	$379$	$\cdots$

看到这里会觉得, 稳定图不就是按照真正的几何对象, 照猫画虎捏出来的小手办, 做出来的 q 版玩具. 那么下面的一些结果将真正揭晓魔法的对应, 就像茵蒂克丝 (自动书记状态) 在小萌老师家用桌子和小道具做出了神殿和天使降临仪式.

——这是这个房间的缩小模型吗?

——使用何种素材都无妨, 只要外型和职责分配无误就可以进行魔法仪式.

命题 1.13. 设 $g,n\ge 0$ 满足 $2g-2+n>0$, 则任意给定亏格 $g$ 具有 $n$ 个标记的稳定图 $\Gamma$:

考虑 ${\overline{M}}_{g,n}$ 中稳定图同构 $\Gamma$ 的曲线等价类集合: $$M^{\Gamma }=\{(C;p_1,\cdots ,p_n):{\Gamma }_C\cong \Gamma \}\subset {\overline{M}}_{g,n},$$它是 ${\overline{M}}_{g,n}$ 中非空, 不可约, 局部闭的子集, 满足$$\dim M^{\Gamma }=\dim {\overline{M}}_{g,n}-\#E(\Gamma ).$$最后, ${\overline{M}}_{g,n}$ 显然是诸 $M^{\Gamma }$ 的无交并. 维数为 $3g-3+n$.

这些 $M^{\Gamma }$ 称为 ${\overline{M}}_{g,n}$ 的阶层 (strata).

为了证明这个定理, 我们的想法实则是从图出发, 相当于拿到了节点曲线 $C$ 的正规化 $\tilde{C}$ 的诸连通分支以及上面的粘接信息, 我们要试图还原出 $C$ 本身. 所以我们需要粘接映射:

命题 1.14. 设 $\Gamma$ 是稳定图, 则存在态射$${\xi }_{\Gamma }:{\overline{M}}_{\Gamma }=\prod _{v\in V(\Gamma )}{\overline{M}}_{g(v),n(v)}\to {\overline{M}}_{g,n}.$$将 $C_v$ 以及其上的标记点打到 $C$, 使得对应的点被粘成节点, 标记点被打到标记点. 而且映射 ${\xi }_{\Gamma }$ 是有限的, 它的像为 $M^{\Gamma }$ 的闭包 ${\overline{M}}^{\Gamma }$.

注意看清楚定理中的上下标, ${\overline{M}}_{\Gamma }$ 是我们在定理中造出来的.

注 1.15. 由此我们实则看出了背后更加奇妙的图景, 整个空间 ${\overline{M}}_{g,n}$ 经由阶层分成了一块一块的, 而这些阶层又几乎和更小的 ${\overline{M}}_{g(v),n(v)}$ 从乘积长得差不多, 所以这些结构也被叫做 ${\overline{M}}_{g,n}$ 的递归边界结构. 这也算是模空间最重要的特性 (feature) 之一. 很多模空间的结论证明都或多或少使用了这一特性.

另外注意一点, 如果某个顶点 $v$ 使得 $g(v)=g,n(v)=n$, 请读者证明这个图中不再有其他顶点和边, 这表明分层是真实有效的, 如果只有一个顶点, 这表明该稳定流形就是光滑的, 不过这时候让我们稍稍怀旧, 看看黎曼是怎么知道模空间的维数的:

黎曼的远见卓识

首先假设 $d$ 是一个很大的待定整数, $X$ 是一个亏格 $g$ 的可定向闭曲面. 我们首先具有一个事实

命题 1.16. 设 $f:X\to M$, 其中 $M$ 是黎曼面 (带有复结构), 而且 $f$ 是拓扑上的分歧覆盖, 则 $X$ 存在唯一的复结构使得 $f$ 是解析的.

证明概要. $M$ 上不包含分歧点的单连通开集, $f$ 原像上的复结构自然存在唯一, 过渡到 $M$ 挖掉分歧点后的万有覆叠空间 $\tilde{M}$ 观察, 即可得知 $\tilde{M}$ 的复结构至多唯一, 不难检查可以下降到 $M$ 上. 于是 $X$ 上除了有限个点外的复结构被确定, 换句话说, 我们现在局部上有 $\mathbb{D}\backslash 0$ 上仅在 $0$ 分歧的映射 $z\mapsto f_0(z)$, 而且在 $\mathbb{D}$ 上连续, 于是 $0$ 看作有界奇点, 所以可去. 自然可以将 $\mathbb{D}$ 上的复结构放在 $M$ 处对应的局部上, 最后因为复结构的连续性所以唯一.

$\square$

命题 1.17 (拓扑 Riemann–Hurwitz). 设 $f:X\to M$ 是拓扑可定向曲面间的分歧覆盖, 且记 $i(x)$ 为 $x\in X$ 的分歧指数, $d$ 为映射次数, 那么$$(2g(X)-2)-d(2g(M)-2)=\sum _{x\in X}i(x).$$反过来符合这个等式的任意 $X,M,d,x,i(x)$, $f$ 总能被构造出来.

证明可以使用三角剖分等手段, 因为技术和本文关系不大而且较长, 故略去.

现在我们令 $M={\mathbb{P}}^1$ 为黎曼球面, 那么 $g(M)=0$ 于是等式成为 $2g+2d-2=\sum i(x)$. 这表明我们可以在 $X$ 上任意取 $2g+2d-2$ 个互不相同的点 $x_1,\cdots ,x_{2g+2d-2}$, 使得分歧指数都是 $1$, 换言之局部为双页分歧. 实际上这才是分歧的一般情况, 高分歧应该在这个参数空间中是 " 更低维数 " 的存在, 现在前一个命题给出我们 $X$ 上的一个可能的复结构. 但是我们知道有很多映射可能对应同一个复结构, 为了确认这一点, 需要使用 Riemann-Roch 定理:

任取 $X$ 上互不相同的 $d$ 个点 $y_i$ 就定义 $X$ 上的除子 $D=\sum y_i$, 显然 $\mathrm{deg}D=d$, 于是$$l(D)=d+1-g+i(D).$$对 $d$ 充分大我们有 $i(D)=0$ 从而 $l(D)=d+1-g$.

我们要构造 $X\to {\mathbb{P}}^1$ 的 $d$ 次 (一般位置) 映射, 其实相当于给出某 $L\in {\mathrm{Pic}}^d(C)$ 的两个线性无关截面, 然后射影化, 射影化使得截面 $(s_1,s_2)$ 和 $(a{s}_1,a{s}_2)$ 构造相同的映射, 维数减 $1$, 于是给定 $L$ 后, $(s_1,s_2)$ 的模空间维数即 $2l(D)-1=2d+1-2g$, 因为只需它们的位置充分一般. 最后注意到 ${\mathrm{Pic}}^d(C)\cong {\mathrm{Pic}}^0(C)$ 是 $g$ 维的, 而且一般位置的 $L\in {\mathrm{Pic}}^d(C)$ 对应的除子都形如 $D$, 这表明 $X\to {\mathbb{P}}^1$ 的映射模空间维数是 $(2d+1-2g)+g=2d+1-g$.

反过来, 任意一个 $X$ 上的复结构都能如上面这样诱导到 $X$ 的分歧映射, 所以 $X$ 上的复结构都是被这么做出来的, 这表明 $X$ 上复结构的模空间, 也正对应着模空间 $M_g$, 维数为: $2g+2d-2$ 减掉对应出同一个复结构的 $2d+1-g$ 者, 所得即 $3g-3$.

问题来了, 所有的计算都很正确, 但是我们知道椭圆曲线的复结构模空间其实是 $1$ 维的, 但是为何 $3\cdot 1-3=0$ 呢? 另一方面所谓的 $3\cdot 0-3=-3$ 又是什么意思呢? 为了说清楚它们, 我们需要弄清楚这三个模问题是什么:

$\bullet$ 首先我们算的第一个量 $2d+2g-2$. 模问题是 $M:=\{X_{\mathrm{top}}\to {\mathbb{P}}^1\}/\sim$ 的全体 $d$ 次拓扑分歧覆盖, 商掉 $\sim$: 同伦等价, 首先因为同伦等价的映射具有相同分歧点, 于是同伦等价的映射, 能提升成去掉分歧点后万有覆叠 $\mathbb{D}$ 到自身的映射, 而 $\mathbb{D}$ 上的复结构唯一 (另一方面同伦群在这种意义上看是离散的, 因此商同伦等价, 和商具有相同分歧点不改变维度), 当然我们真正关心的是 $X_{\mathrm{top}}$ 上由此方法得到的一个复结构, 第一个量正是这一模空间的维数 $2d+2g-2$.

$\bullet$ 第二个量 $2d+1-g$. 模问题是给定 $X$ 一个具体复结构后, $M^{\prime }:=\{X_{\mathrm{cpx}}\to {\mathbb{P}}^1\}$ 的全体 $d$ 次解析映射, 此模空间维数为 $2d+1-g$.

$\bullet$ 而我们关心的所谓 $1$ 维的复结构, 是 $M^{\prime \prime }:=\{X_{\mathrm{top}}/X_{\mathrm{cpx}}\}$, 相当于给 $X$ 安装复结构的维数.

问题出在第一个数减去第二个数不等于 $1$, 第一个模问题和第三个模问题在 $X_{\mathrm{cpx}}$ 的自同构下表现相同: 自同构即所谓的椭圆曲线上的加法 $X\mapsto X+P$. 但是第二个问题不允许, 因为在自同构下不同的函数真的是不同的函数. 如果我们把第二个模问题换成 $\{X_{\mathrm{cpx}}\to {\mathbb{P}}^1\}/\mathrm{Aut}(X_{\mathrm{cpx}})$, 那么它们实则也对应了第一个模问题中相同的复结构, 这样才真的有它们的差是 $1$. 而巧的是, 这些自同构在第二个模问题上, 恰好贡献了 $1$ 个复维数. 换言之 $\mathrm{Aut}(E)$ 是 $1$ 维的, 这才真正解释了这里的差别. 根据这正确的商的形式: $M/(M^{\prime }/\mathrm{Aut}(X_{\mathrm{cpx}}))=M^{\prime \prime }$, 我们得到更加一般的: $$3g-3+{\dim }_{\mathbb{C}}\mathrm{Aut}(X_{\mathrm{cpx}})={\dim }_{\mathbb{C}}(X_{\mathrm{top}}/X_{\mathrm{cpx}}).$$这不仅解释了 $g=0,1$ 时的现象, 还为我们将来讨论模叠做准备.

本质上说, 正确的模空间对象是一个纤维丛, 底空间是复结构即复 $1$ 维的 $\mathbb{H}/\mathrm{PGL}(2,\mathbb{Z})$, 每个纤维是 " 复 $-1$ 维的 "$\mathbf{B}E$, 由此整个东西是 $3\cdot 1-3=0$ 维的.