2. 从图的分割出发
此部分主要参考自文章 A Tutorial on Spectral Clustering 的 Section 2, 3, 5.
建模: 将数据点 之间的相似度 [similarity] , 可以表示为一个 阶的带权无向图 [similarity graph] , 其每条边 的权重 表示 的相似程度.
目的: 给出图 的一个分割, 使得组间边的权重尽可能低, 同时各组内边的权重尽可能高.
2.1图的基本概念
给定一个带权的无向图 , 其权重可以排成一个对称矩阵 , 称为带权邻接矩阵 [Weighted adjacency matrix] . 由此可以定义顶点 的度 , 排成一个对角阵 , 称为度矩阵 [Degree matrix] .
对于 的子集 , 我们可以定义其指示向量 [Indicator vector] 为 , 其中 当且仅当 , 简记为 . 其在 中的补集表为 . 两个子集之间连边的权重之和
2.2图的分割
最简单直接的方式是最小割方法 [mincut approach] : 其中的 是因为每条边都计算了两遍.
这样定义的问题往往较为简单 (特别当 时) , 可以被高效解决. 但它往往将单点分割开, 这并不是 “聚类” 所希望得到的结果!
因此, 我们希望得到的 都适当大, 而子集的大小一般有两种衡量方式:
• | 顶点个数 |
• | 顶点度的和, 即与之相关联边的权重之和, 也称 “体积” |
故引入如下两个目标函数 RatioCut 和 normalized cut:
注意到其中等式成立 (取得最小值) 分别当且仅当 都相等、 都相等. 因此直观上看, 这两个目标函数都是希望让 “聚类” 的结果更加 “平衡” [balanced] . 这就是我们想要的!
然而, 这两个优化问题都是 NP-hard 的, 这意味着我们目前普遍相信不能在多项式时间内准确求解. 因此我们考虑对它们作近似求解. 谱聚类就是对这两个目标函数作松弛 [relaxation] 的近似求解方法.
2.3对 RatioCut 的松弛
基础情形:
我们的目标函数是先尝试将其计算出来. 其中其中 是由 各行和组成的向量, 即 , 于是因此 , 于是
为了方便求解其最小值, 我们考虑将与 有关的系数和指示向量 合并, 从而用一个向量 来表示 这个极小化变量. 我们看只要 仍是某种 “指示向量”, 那么当 同属于 或 时, 应有 , 从而其中的 一项应是常值, 先记为 , 则 , 从而根据我们的目的, 注意到 , 我们将上式化为因此只需让 即可.
这仍然使得 有不同选择, 我们再由上述得到的可知 是 关于特征值 0 的特征向量. 又而一般来说, 图 是连通的 (否则问题平凡) , 从而每个 , 故有 , 即 . 而 是对称阵, 故 0 是其单特征值. 因此, 只要我们取 , 就有 的最小值在 为第二特征向量 (第二小特征值对应的特征向量) 时取到.
因此我们取则有并且从而原优化问题可以等价地表为这仍然是一个离散的优化问题, 仍是 NP-hard 的. 最简单的松弛就是去掉离散的约束, 成为正如刚才所说, 其最优解 即为模为 的第二特征向量. 为了最终得到图的分割, 我们还需要回到离散的原问题, 最简单的方式是看 各分量的符号, 将符号为正的指标归入 . 但是, 为了将这个算法推广到一般的 , 这个方式显然过于简单. 因此在谱聚类算法中, 我们采用 K-means 方法对 的分量在 中进行聚类, 从而形成图的分割.
一般情形:
显然我们不能像一开始那样去化简目标函数, 但我们仍然想用 的二次型来表示目标函数. 我们已经有故只要取从而目标函数化为其中 各列相互正交, 从而 . 仍然去掉对 的离散约束, 得到松弛的优化问题
这是一个等式约束问题, 我们可以用 Lagrange 乘子法求解之: 先将约束条件写成向量形式然后得到 Lagrange 函数为其中 . 其驻点 满足将这些条件写成一个矩阵 (其实就是矩阵函数的微分记号) , 即为其中 是 阶对称阵, 可作对角化, 即存在同阶正交阵 及对角阵 使得令 , 则 , 并且故 也是松弛优化问题的解. 最优化条件化为 , 故 的列即为 的 个互相正交的特征向量, 并且的最小值当 的对角元是 的前 个特征值时取到, 故最优解 由 的前 个特征向量组成. 最后, 和上述同理, 我们对 的 个行向量作 K-means 聚类, 形成图的分割. 此即非规范的谱聚类算法 [Unnormalized Spectral Clustering] .
回到上述 的情形, 的前两个特征向量为 , 其 个二维的行向量其实只有第二个分量是不同的, 确实只需对该分量在 上作聚类.
2.4对 Ncut 的松弛
将上面的 都换成 就可以得到相应的结果. 直接看一般情形: 取则由
可知 . 易见 , 故有 . 仍然去掉对 的离散约束, 并作换元 , 得到松弛的优化问题利用前面的结果, 可知其最优解 由 的前 个特征向量组成. 此即由此也可见 与 具有相同的特征值, 并且相应的特征向量只差一个坐标变换 . 故最优解对应的 由 的前 个特征向量组成, 也即广义特征值问题 的前 个广义特征向量. 回到离散问题的方式与上一方法相同, 此即规范的谱聚类算法 [Normalized Spectral Clustering] .
2.5评价
“松弛 + 离散化” 这个过程不能保证得到原问题的最优解, 甚至可能距离很远. 看一个例子:
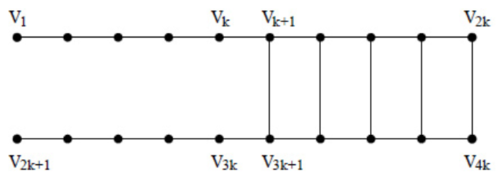
例 (蟑螂图 [The cockroach graph] ).
作 聚类:
• | 原 RatioCut 问题的最优解: 竖直从中间劈开, 有 ; |
• | 非规范松弛方法: 简单用 的第二特征向量分量的正负来分类, 可以得到最优解为: 水平从中间劈开, 有 ; |
当 很大时, 这两个解的差别是巨大的!
虽然如此, 我们还是对谱松弛的方法感兴趣. 之所以这样, 不是因为它给出很好的结果, 而是因为它给出了易于求解的标准线性代数问题.