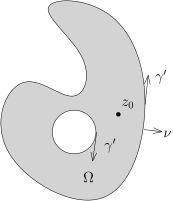
假设 Ω⊂C 是开集, K⊂Ω 是有界带边区域 (特别地, K 是紧的) , 其边界 γ=∂K 是 C1 曲线 (可以有多个连通分支) .
我们已经对复解析函数 F(z) 证明了 Cauchy 积分公式: 如果 F(z) 在 Ω 上是复解析的, 那么, 对于 z0∈K˚ (K 的内部) , 我们有F(z0)=2πi1∫γz−z0F(z)dz.
利用 Cauchy 公式, 我们证明, 复解析函数是 “解析” 的, 也就是说可以在如下意义下写成幂级数的形式:
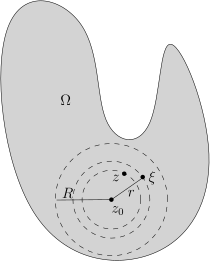
假设 F 为开集 Ω⊂C 上的复解析函数, 并且以 z0 为圆心以 R 为半径的开球 BR(z0)⊂Ω. 那么, F(z) 在 z0 处的解析半径至少是 R, 也就是说, 在 BR(z0) 上, 我们有F(z)=a0+a1(z−z0)+a2(z−z0)2+⋯+an(z−z0)n+⋯,其中ak=2πi1∫∣ξ−z0∣=r(ξ−z0)kF(ξ)dξ, r<R.这里, 等式右边的幂级数对任意的 z∈BR(z0) 都是收敛的. 上面系数定义中的 r 可以是 (0,R) 中的任意一个数.
证明的想法很简单: 我们把 Cauchy 积分公式
F(z)=2πi1∫γξ−zF(ξ)dξ的右边的积分项强行展开即可.
证明. 我们选取一个正实数
r, 使得
∣z−z0∣<r<R. 我们任意给定
ξ, 使得
∣ξ−z0∣=r.
此时, 我们有
ξ−z1=(ξ−z0)−(z−z0)1=ξ−z011−ξ−z0z−z01=k=0∑∞(ξ−z0)k+1(z−z0)k.在上面的式子中, 由于
∣∣ξ−z0z−z0∣∣<1, 所以, 我们有 (级数收敛) :
1−ξ−z0z−z01=k=0∑∞(ξ−z0z−z0)k.这些级数显然是绝对收敛的, 从而与积分可交换 (也可以利用 Lebesgue 控制收敛定理) . 所以, 代入 Cauchy 积分公式, 我们就得到
F(z)=2πi1∫∣ξ−z0∣=rk=0∑∞F(ξ)(ξ−z0)k+1(z−z0)kdξ=k=0∑∞(2πi1∫∣ξ−z0∣=r(ξ−z0)k+1F(ξ)dξ)(z−z0)k比较系数, 这就给出了定理的证明.
这里的假设与定理中是一致的. 我们进一步假设 Ω 是道路连通的, 即对任意的 z1,z2∈Ω, 存在连续映射γ:[0,1]→Ω, t↦γ(t),使得 γ(0)=z1,γ(1)=z2. 那么, 复解析函数 F 在 Ω 中的零点是离散的 (即如果 z0 是 F 的一个零点, 那么, 存在 ε>0, 使得对任意的 z, ∣z−z0∣<ε, F(z)=0) , 除非 F≡0.
特别地, 给定 Ω 上的两个复解析函数 F 和 G, 如果 F 和 G 在 Z⊂Ω 上取值相同, 并且 Z 在 Ω 中有聚点, 那么, F≡G.
证明. 假设 z0 是 F 的一个零点, 即 F(z0)=0. 根据 F 的解析表达式, 在 BR(z0)⊂Ω 上, 我们有F(z)=a0+a1(z−z0)+a2(z−z0)2+⋯+an(z−z0)n+⋯.如果这些系数 ai 全部为 0, 那么, F 在 BR(z0) 上恒为 0; 否则, 假设 am 是第一个不是 0 的系数, 那么, 我们有F(z)=(z−z0)m(am+am+1(z−z0)+am+2(z−z0)2+⋯)=(z−z0)mG(z).根据定理的证明, 级数G(z)=am+am+1(z−z0)+am+2(z−z0)2+⋯也是绝对收敛的, 特别地, 这是连续的, 所以, 当 z=z0 时, G(z0)=am=0. 从而, 存在 δ, 使得 G 在 Bδ(z0) 上不会等于 0, 此时, 我们知道, F 在 z0 的附近 (Bδ(z0) 上) 恰好有一个零点.
我们现在证明, 如果 F 在 z0 的一个邻域 Bδ(z0) 上恒为 0, 那么, F 在 Ω 上恒为 0: 任意选取 z1∈Ω 和曲线γ:[0,1]→Ω, t↦γ(t),使得 γ(0)=z0,γ(1)=z1. 令t∗=sup{t∈[0,1]∣∣F(γ(t))∣∣[0,t]≡0}.由于 F 在 z0 的一个邻域 Bδ(z0) 上恒为 0, 所以, t∗>0. 我们现在证明 t=1: 如果假设 t∗<1, 根据连续性, 我们知道 F(γ(t∗))=0. 根据前面的构造, 由于 F 在 γ(t∗) 的任意一个小邻域中都有零点 (因为和 γ−1([0,t∗]) 相交) , 根据之前的推导, 存在 γ(t∗) 一个邻域 Bδ1(γ(t∗)), 使得 F 在 Bδ1(γ(t∗)) 上恒为 0, 根据连续性, 那么, 存在 ε>0, 使得 F(γ(t))∣∣[0,t∗+ε]≡0, 这和 t∗ 的最大性矛盾.
由于 t∗=1, 所以, F(z1)=0, 这就证明了在 Ω 上, F≡0.
这里的假设与定理中是一致的. 那么, F 的 n 次导数 F(n) 仍然是解析函数. 我们进一步有如下的公式: F(n)(z)=2πin!∫∣ξ−z∣=r(ξ−z)n+1F(ξ)dξ.特别地, 我们有如下的导数估计: ∣F(n)(z)∣⩽rnn!∣ξ−z∣=rsup∣F(ξ)∣.
证明. 我们将
F 在
z0=0 (不妨) 处展开为级数
F(z)=a0+a1z+a2z2+⋯,其中, 我们假设上面的级数的收敛半径至少是
R>0, 即对于
∣z∣<R 都是绝对收敛的. 根据定理中系数的计算, 我们知道
∣ak∣⩽rk1∣ξ∣=rsup∣F(ξ)∣⩽rk1M, r<R.其中,
M 为
∣F∣ 在半径为
r 的圆圈上的最大值. 从而, 对
∣z∣⩽r′<r, 对任意的
k⩾0, 我们有
∣kakzk−1∣⩽Mbkrk∣∣rr′∣∣k−1.当
k 足够大的时候, 比如说
k>k0=⌊(1−rr′)−1⌋时, 我们有
bkbk+1=(1+k1)rr′<1,所以,
{bk}k⩾k0 可以被一个公比小于
1 几何级数来控制, 从而, 级数
a1+2a2z1+3a3z2+⋯在
∣z∣<r′ 时是绝对收敛, 这表明可以逐项求微分 (根据 Lebesgue 控制收敛定理的推论) . 这说明
F′(z)=a1+2a2z1+3a3z2+⋯对于
∣z∣<r′<r<R 成立. 由于
r′ 和
r 是任意选取的, 所以, 上面的的式子对于
∣z∣<R 都成立. 特别地, 我们证明了
F′(z0)=a1.由归纳法, 对任意的
k, 我们就有
F(k)(z0)=k!ak.再根据定理中的计算, 这就证明了这个推论叙述中的公式. 导数估计是显然的.
假设 F(z) 是在整个 C 上定义的复解析函数 1. 如果 F 是有界函数, 那么 F 是常值函数.
证明. 我们只要证明 F′(z)≡0 即可: 根据 F 在一点处的展开, F′(z)≡0, 意味着定理中的系数a1=2a2=3a3=⋯=0.所以, F 在一点附近恒为 a0, 从而 F 为常数 (一点附近的邻域有聚点) .
我们利用导数估计:
∣F′(z)∣⩽r1∣ξ−z∣=rsup∣F(ξ)∣⩽r∥F∥∞.由于
F 在整个
C 上定义, 从而可以将
r 取得任意大, 这表明对任意的
z∈C,
F′(z)=0.
对任意的次数非零的复系数多项式P(z)=zn+an−1zn−1+⋯+a1z+a0,它在 C 上必有一个根.
证明. 我们观察到
P 在整个
C 上是复解析的, 并且当
∣z∣→∞ 时, 我们有
∣P(z)∣→∞.我们用反证法: 如若不然,
F(z)=P(z)−1是在全平面
C 上良好定义的函数. 另外, 我们有
∂(F)=−P(z)−2∂P=0.所以,
F 是复解析的. 另外, 当
∣z∣→∞ 时, 我们还有
∣F(z)∣→0.这说明,
F 是有界的. 根据 Liouville 定理,
F 为常数, 从而
P 也是, 那么它的次数是
0, 矛盾.
Cauchy 积分公式是复分析中最重要的公式, 除了用来证明解析性, 它还有其他众多重要的推论, 比如说关于复解析函数的极大模原理:
假设 F(z) 是区域 Ω⊂C 上的复解析函数, 那么 ∣F(z)∣ 的最大值, 如果能取到的话, 一定在 Ω 的边界 ∂Ω 上取到. 进一步, 如果 ∣F∣ 在 Ω 的内部有最大值点, 那么 F 一定是常值函数.
证明. 假设 z0∈Ω˚ 是 ∣F∣ 的最大值点, 即∣F(z0)∣=z∈Ωsup∣F(z)∣.根据 Cauchy 积分公式, (选取较小的 ε, 使得 Bε(z0)⊂Ω, 下面的的 r 只要满足 r<ε 即可) 我们有∣F(z0)∣=∣∣2π1∫02πF(z0+reiθ)dθ∣∣⩽2π1∫02π∥F∥L∞dθ=2π1∫02π∣F(z0)∣dθ=∣F(z0)∣.这表明, 上述不等式必须处处取等号, 这表明在 z0 的整个邻域 Bε(z0) 上, ∣F(z)∣ 为常数.
我们现在证明
F 在
Bε(z0) 上为常数, 不妨假设
z0=0. 如若不然, 那么, 我们当
ε 较小时, 我们有解析表达式
F(z)=a0+zm(am+am+1z+am+2z2+⋯),其中
am=0. 通过对
F(z) 乘以一个常数, 我们还可以假设
a0>0 (如果
a0=0, 那么
∣F∣ 在
z0 附近恒为零) . 选取
ξ, 使得
ξm=−am, 所以, 对于比较小的
δ>0, 我们有
F(δξ)=a0−δm∣am∣2+O(δm+1).令
δ→0, 这就和
∣F(z0)∣ 最大矛盾. 所以,
F 在
Bε(z0) 上为常数, 所以
F 为常数.
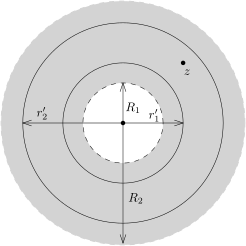
F 是环面 {z∈C∣∣R1<∣z∣<R2} (我们经常取 R1=0) 上的复解析函数. 对每个整数 k∈Z, 对任意的 R1<r<R2, 我们定义ak=2πi1∫∣z∣=rzk+1F(z)dz=2πrk1∫02πe−ikθF(reiθ)dθ.那么, 对任意满足 R1<∣z∣<R2 的 z, 我们有 (对每个固定的 z, 以下的级数绝对收敛) F(z)=k=−∞∑∞akzk.
证明. 根据 Cauchy 积分公式, ak 与 r 在 (R1,R2) 中的选择无关. 我们选取R1<r1′<r1<∣z∣<r2<r2′<R2并令 Ci′ 为半径为 ri′ 并且中心在原点的圆, 其中 i=1,2. 根据 Cauchy 积分公式, 我们有F(z)=2πi1∫C2′ξ−zF(ξ)dξ−2πi1∫C1′ξ−zF(ξ)dξ.我们重复之前证明复解析函数能做解析展开的做法.
对于第一项, 由于对任意的
ξ∈C2′, 我们有
∣z∣<∣ξ∣, 我们有
ξ−z1=ξ11−ξz1=ξ1k=0∑∞(ξz)k.第二项之中, 由于
∣z∣>∣ξ∣, 其中
ξ∈C1′, 我们有
ξ−z1=−z11−zξ1=−z1k=0∑∞(zξ)k.将上面的两个展开代入
F(z) 的表达式, 我们就有
F(z)=2πi1∫C2′ξF(ξ)k=0∑∞(ξz)kdξ+2πi1∫C1′zF(ξ)k=0∑∞(zξ)kdξ.将求和与积分交换就得到了要证明的结论.
假定 F(z) 在区域 {z∣∣0<∣z−z0∣<r} 上是复解析的, 其中 r>0, 它的 Laurent 展开为F(z)=k=−∞∑∞akzk.我们称其中的 z−1 的系数 a−1 为 F 在 z0 处的留数, 并记作 Res(F;z0).
按照定义, 我们有Res(F;z0)=2πi1∫∣z−z0∣=rF(z)dz.这因为 Laurent 展开中其它幂次的积分都是 0.
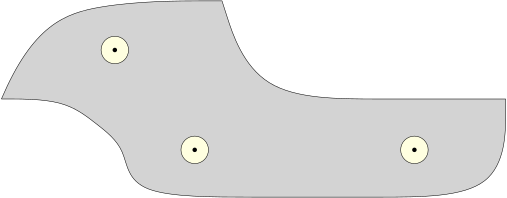
假定 Ω⊂C 是一个紧区域, Ω 边界为分段光滑的 C1-曲线. 除去点 z1,⋯,zN∈Ω˚ 之外, F 为 C−{z1,⋯,zN} 上的复解析函数, 那么, k=1∑NRes(F;zk)=2πi1∫∂ΩF(z)dz.
证明. 对每个
k⩽N, 先将每个
zk 附近的小圆盘
Bε(zk) 从
Ω 上抠掉, 使得
z∈Ω−⋃k⩽NBε(zk). 我们在区域
Ω−⋃k⩽NBε(zk) 上用 Cauchy 积分公式.
考虑到曲线的定向, 我们有
2πi1∫∂ΩF(z)dz−k=1∑N2πi1∫∂Bε(zk)F(z)dz=0.所以,
2πi1∫∂ΩF(z)dz=k=1∑N2πi1∫∂Bε(zk)F(z)dz=k=1∑NRes(F;zk).这就证明了留数定理.
我们试举一个有趣的应用, 其它在计算上的应用我们将在 Fourier 变换的一部分再做演示.
我们在第一学期已经定义了三角函数cos(z)=21(eiz+e−iz), sin(z)=2i1(eiz−e−iz).我们研究 sin(z) 的零点, 即找到 z0, 使得eiz0−e−iz0=0 ⇔ e2iz0=1 ⇔ z0∈πZ.对任意的 a∈/Z, 我们考虑F(z)=(z−a)2πcot(πz)=sin(πz)(z−a)2πcos(πz).那么, F(z) 不解析的地方只能是 a 和 n∈Z.
在 z=a 处, 要想有非平凡的留数, cot(πz) 需要贡献一个 z−a 的因子, 所以Res(F;a)=(πcot(πz))′∣z=a=−sin2(πa)π2.
在 z=n 处, 由于 sin(πz)′∣∣z=n=0, 所以, sin(πz) 的零点是 1 阶的, 据此, 我们知道Res(F;n)=(n−a)21.
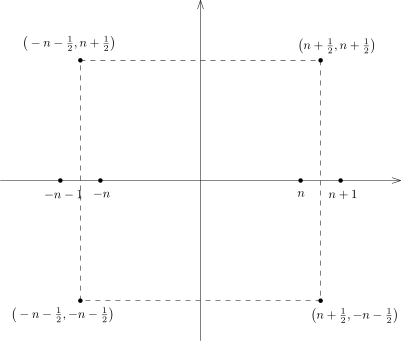
我们对于顶点在
(±(n+21),±(n+21)) 的正方形
Qn 上用留数定理, 其中,
n 足够大使得
a∈Qn. 所以,
∣k∣⩽n∑(k−a)21−sin2(πa)π2=2πi1∫∂Qnsin(πz)(z−a)2πcos(πz)dz.利用
z=x+iy, 我们很容易看出
sin(πz)(z−a)2πcos(πz)=O(n21).所以上面的积分项的贡献为
2πi1∫∂Qnsin(πz)(z−a)2πcos(πz)dz=O(n1).令
n→∞, 我们就得到了
n∈Z∑(n−a)21=sin2(πa)π2.利用上面例子中的分析, 我们还可以证明 Euler 的著名公式. 首先, 在 C−Z 上的任意一个紧集上, 级数f(z)=n∈Z∑(z−n)21是一致收敛的, 所以, f(z) 是 C−Z 上的复解析函数 (可逐项求导数) . Euler 观察到, 函数g(z)=sin2(πz)π2也是 C−Z 上的复解析函数. 进一步, 由于 sin(πz) 的零点是单零点, 所以, g(z) 在每个 n∈Z 处的 Laurent 展开的负幂和 f(z) 的是一致的. 所以, F(z)=g(z)−f(z)=sin2(πz)π2−n∈Z∑(z−n)21是全平面上定义的复解析函数并且具有周期性 F(z+1)=F(z).
对于任意的 x∈[0,1], 我们很容易证明下面的极限: ∣y∣→∞limF(x+iy)=0.利用周期性, 我们就知道 F 是有界的, 从而根据 Liouville 定理, 我们得到 F≡0. 这表明sin2(πz)π2=n∈Z∑(z−n)21.稍加变形, 我们有sin2(πz)π2−z21=n=0∑(z−n)21.左右在 z=0 处取极限, 我们就证明了著名的 Euler 公式: 121+221+321+421+⋯=61π2.