基本习题
习题 A: 中值定理和 Taylor 展开
如果不额外说明, f 总代表一个区间 I 上定义的函数.
A1) | 设 f 在点 x 处有二阶导数. 证明, 下面的极限给出了二阶导数: f′′(x)=h→0limh2f(x+h)+f(x−h)−2f(x) |
A2) | (Taylor 展开式的唯一性, Peano 余项) . 假设 f 是在 x0 附近的函数, 并且当 x→x0 时, 满足f(x)=a0+a1(x−x0)+a2(x−x0)2+⋯+an(x−x0)n+o(∣x−x0∣n)=b0+b1(x−x0)+b2(x−x0)2+⋯+bn(x−x0)n+o(∣x−x0∣n)其中 ai,bi,i=0,⋯,n 是实数, 那么, 对任意的 i, 我们都有 ai=bi. |
A3) | 假设 f 在 0 处有 n 阶导数. 证明, 如果 f(x) 是偶函数 (奇函数) , f 在 0 处的 Taylor 展开式 (Peano 余项) 中只有 x 的偶次项 (奇数项) . |
A4) | (Rolle 定理的简单推广) 设函数 f 在有限或无穷的区间 (a,b) 上可微并且 x→a+limf(x)=x→b−limf(x). 证明, 存在 x0∈(a,b), 使得 f′(x0)=0. |
A5) | 设函数 f∈C0([a,b]) 并且在 (a,b) 上可微. 证明, f 在 [a,b] 上严格递增的充分必要条件是对任意 x∈(a,b), f′(x)⩾0 并且在任意子区间 (c,d)⊂(a,b) 上, f′(x) 不恒等于 0. |
A6) | g∈C(R) 在 R 上可微. 假设存在常数 M, 使得 x∈Rsup∣g′(x)∣⩽M. 对任意的 ε>0, 我们定义fε(x)=x+εg(x).证明, 存在仅依赖于 M 的常数 δ=δ(M)>0, 使得当 ε<δ 时, f:R→R 是双射. |
A7) | 设函数 f 在 [a,b] 上有两阶导数并且 f′(a)=f′(b)=0. 证明, 存在 c∈(a,b) 使得∣f′′(c)∣⩾(b−a)24∣f(b)−f(a)∣ |
A8) | 假设 f 在 R 上二次可导, 对 k=0,1,2, 我们假设 Mk=x∈Rsup∣f(k)(x)∣ 都是有限的. 证明, M12⩽2M0M2. |
A9) | 假设 f 在 (0,+∞) 上二次可导, f′′ 在 (0,+∞) 上有界并且 x→+∞limf(x)=0. 证明, x→+∞limf′(x)=0. |
习题 B: L’Hôpital 法则
用 L’Hôpital 法则求极限: (1)(4)(7)(10)(13)(16)x→+∞limxalogx,a>0x→0limx−sinxtanx−xx→1−limlog(x)log(1−x)x→1limx1−x1x→0lim(xsinx)1/(1−cosx)x→+∞lim(logx)xxlogx(2)x→+∞limbxxa,a>0,b>1(5)x→0limx2sinx21−cosx2(8)x→0+limlogsinbxlogsinax,a,b>0(11)x→1lim(logx1−x−11)(14)x→alimx−aax−xa,a>0(17)x→+∞lim[(x+a)1+1/x−x1+x+a1](3)x→0limsinax−sinbxeax−ebx(6)x→1lim1−x4/32x−x4−3x(9)x→0+limxx(12)x→0+lim(sinx)x(15)x→+∞lim1/x(1+1/x)x−e(18)x→+∞lim[3x3+x2+x+1−x2+x+1⋅xlog(ex+x)]
习题 C: 函数最值
求下列函数在给定区间上的最大值和最小值:
1) | f(x)=x4−2x2+5, x∈[−2,2]; 2) f(x)=1+x22x, x∈R; |
3) | f(x)=arctanx−21log(1+x2); 4) f(x)=xlogx, x∈(0,+∞); |
5) | f(x)=xlogx, x∈(0,+∞); 6) f(x)=2tanx−tan2x, x∈[0,2π). |
习题 D: 极大值的判定, 重要
f 在 (a,b) 上可微. 假设对于 x0∈(a,b), 我们有 f′(x0)=0.
D1) | 证明, f 在 x0 处取局部极大值的一个充分条件是: 存在某一邻域 (x0−δ,x0+δ)⊂(a,b), 使得f′(x)={>0, 对所有的 x∈(x0−δ,x0);<0, 对所有的 x∈(x0,x0+δ). |
D2) | (最重要的判别方法, 有很多应用) 证明, 如果 f′′(x0) 存在并且 f′′(x0)<0, 那么 f 在 x0 处取局部极大值. |
D3) | 假定 f 在 x0 处有 n 阶导数, f′(x0)=⋯=f(n−1)(x0)=0 并且 f(n)(x0)=0, 试讨论 f 在 x0 处取局部极大值的条件 (对 n 分奇偶讨论) . |
习题 E: 多项式的根
(提示: 利用中值定理和 n-次的多项式至多 (恰好) 有 n 个根)
E1) | 证明, 如果实系数多项式 Pn(x)=anxn+an−1xn−1+⋯+a0 的根都是实数 (不妨设 an=0) , 那么它的逐次导函数 Pn′(x), Pn′′(x) , ⋯, Pn(n−1)(x) 的根也都是实数. |
E2) | 证明, Legendre 多项式 Pn(x)=2nn!1dxndn(x2−1)n 的根都是实数并且包含于区间 (−1,1) 中. |
E3) | 证明, Ln(x)=n!exdxndn(e−xxn) 是多项式 (被称作是 Laguerre 多项式) 并且它所有的根都是正实数. |
E4) | 证明, Hn(x)=(−1)nex2dxndn(e−x2) 是多项式 (被称作是 Hermite 多项式) 并且它所有的根都是实数. |
习题 F: Émile Borel 引理
第一部分: 截断函数的构造
F1) | 定义函数 ϕ:R→R: ϕ(x)={e−x21, x>0;0, x⩽0.证明, ϕ∈C∞(R). |
F2) | 定义函数 χ:R→R: χ(x)=ϕ(2−∣x∣)+ϕ(∣x∣−1).ϕ(2−∣x∣)证明, χ(x)∈C∞(R) 并且 χ∣∣[−1,1]≡1, χ∣∣(−∞,−2]∪[2,∞)≡0, 0⩽χ(x)⩽1 并且是偶函数. |
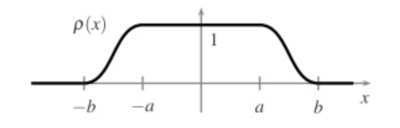
F3) | 证明, 对任意的 0<a<b, 存在光滑偶函数 ρ(x)∈C∞(R), 使得 ρ∣∣[−a,a]≡1, ρ∣∣(−∞,−b]∪[b,∞)≡0, 0⩽ρ(x)⩽1. |
F4) | 证明, 存在偶函数 ψ∈C∞(Rn), 使得 ψ∣∣{x∣∣x∣⩽1}≡1, ψ∣∣{x∣∣x∣⩾2}≡0, 0⩽ψ(x)⩽1. |
第二部分: 逐项求导定理
I=[a,b] 是闭区间, {fk}k⩾0 是 C1(I) 的一列函数, 我们假设 k=0∑∞fk 在 I 上逐点收敛, 即对任意的 x∈I, k=0∑∞fk(x) 收敛, 我们记 f(x)=k=0∑∞fk(x).
F5) | 我们假设函数级数 k=0∑∞fk′(x) 在 I 上绝对收敛, 即数项的级数 k=0∑∞∥fk′∥∞ 收敛, 其中 ∥f∥∞=x∈Isup∣f(x)∣. 证明, f 是可导的并且 f′(x)=k=0∑∞fk′(x). (提示: 设法将求和拆成 k=0∑∞=k=0∑N+k=N+1∑∞) |
F6) | (逐项求导定理) I=[a,b] 是闭区间, {fk}k⩾0 是 C1(I) 的一列函数, 我们假设 k=0∑∞fk 在 I 上逐点收敛. 如果函数级数 k=0∑∞fk′(x) 在 I 上一致收敛, 那么 f 是可导的并且 f′(x)=k=0∑∞fk′(x). |
F7) | 试利用逐项求导定理计算 ex 的导数. |
第三部分: Borel 引理的证明
我们现在任意给定一个数列 {ak}k⩾0.
F8) | 对任意给定的正数 tk>0, 试计算函数 fk(x)=k!akxkχ(tkx) 在 x=0 处的任意阶导数 (包括零阶) . |
F9) | 证明, 当 k⩾2n 时, 我们有fk(n)(x)=akℓ=0∑n(ℓn)(k−ℓ)!tkn−ℓxk−ℓχ(n−ℓ)(tkx). |
F10) | (Borel 引理) 任意给定一个数列 {ak}k⩾0, 证明, 存在 R 上的光滑函数 f, 使得对任意的 k⩾0, f(k)(0)=ak. (提示: 略难. ) |
第四部分: Peano 对 Borel 引理的证明 (选做部分, 不交作业)
F11) | {ck}k⩾0 和 {bk}k⩾0 是两个序列, 其中 bk 都是正数. 证明, (1+bkx2ckxk)(n)(0)={n!(−1)jcn−2jbn−2jj, 若 k=n−2j,j∈Z⩾0;0, 其它情形. |
F12) | 证明, 存在常数 C, 对任意的 k⩾n+2, 对任意的 x, 我们有∣∣(1+bkx2ckxk)(n)(x)∣∣⩽C(n+1)!bk∣ck∣k!∣x∣k−n−2. |
F13) | 证明, 当 {ck}k⩾0 给定的时候, 我们可以选取 bk, 使得 bk 仅依赖于 ck 的选取, 并且函数级数 f(x)=k=0∑∞1+bkx2ckxk 是无限次可微分的. |
F14) | 证明, f(0)=c0, f′(0)=c1, 并且当 n⩾2 时, 我们有n!f(n)(0)=cn+j=1∑⌊2n⌋(−1)jcn−2jbn−2jj. |
F15) | 证明, 我们可以通过恰当的选取 {ck}k⩾0 和 {bk}k⩾0 来证明 Borel 引理. |
期中考试题目 B
以下为上学期期中考试的 B 部分, 供同学参考, 不交作业
考虑在整个实数上定义的函数 f:R→R.
• | 如果存在正实数 A (不是无穷) , 使得对任意的 x∈R, 都有 ∣f(x)∣⩽A, 我们就称 f 是有界的. 我们将 R 上定义的所有有界函数的集合记作 B. |
• | 如果存在正实数 B (不是无穷) , 使得对任意的 x,y∈R, 都有 ∣f(x)−f(y)∣⩽B∣x−y∣, 我们就称 f 是 Lipschitz 函数. 我们将 R 上定义的所有 Lipschitz 函数的集合记作 L. |
假设 a,λ∈R, f∈B∩L, 这个问题的目的是找到一个函数 F∈L 来解下面的函数方程: F(x)−λF(x+a)=f(x), x∈R.(⋆)
第一部分: Lipschitz 函数的基本性质
B1) | 证明, 如果 f,g∈B∩L, 那么它们的乘积 fg∈L. |
B2) | 证明, 如果 f 是 R 上的可微函数并且 f∈L, 那么 f′∈B. |
B3) | 证明, 如果 f 是 R 上的可微函数并且 f′∈B, 那么 f∈L. |
B4) | 如果 f∈B 并且存在正实数 B, 使得对任意的 x,y∈R, ∣x−y∣⩽1, 我们都有 ∣f(x)−f(y)∣⩽B∣x−y∣, 证明, f∈L. |
第二部分: ∣λ∣<1 时方程 (⋆) 的解
此后我们设 f∈B∩L. 我们在这一部分假设 ∣λ∣<1.
B5) | 假设 F 满足 (⋆), 证明, 对任意的 x∈R 和 n∈Z⩾1, 我们都有F(x)=λnF(x+na)+k=0∑n−1λkf(x+ka) 和 F(x)=λ−nF(x−na)−k=1∑nλ−kf(x−ka).请任选其一来证明即可. |
B6) | 证明, 对任意的 x∈R, 级数 k⩾0∑λkf(x+ka) 是收敛的. |
B7) | 根据上述, 对每个 x∈R, 我们定义 F(x)=k⩾0∑λkf(x+ka). 证明, F∈L 并且解方程 (⋆). |
B8) | 证明, 如果 F1,F2∈L 都满足方程 (⋆), 那么 F1=F2. |
B9) | 在 (⋆) 中取函数 f(x)≡1, 试求方程的解 F1; 在 (⋆) 中取函数 f(x)=cos(x), 证明, F2(x)=1−2λcos(a)+λ2cos(x)−λcos(x−a) 是 (⋆) 的解. |
第三部分: ∣λ∣>1 时方程 (⋆) 的解
B10) | 参照第二部分的结论, 试陈述当 ∣λ∣>1 时应当如何来解方程. 你的陈述不要超过 100 个汉字. |
B11) | 当 ∣λ∣>1 时, 在 (⋆) 中取函数 f(x)≡1, 试求方程的解 F1; 当 ∣λ∣>1 时, 在 (⋆) 中取函数 f(x)=cos(x), 试求 (⋆) 的解 F2(x). |
第四部分: ∣λ∣=1 时的情形.
B12) | 假设 λ=1. 证明, 存在非零的函数 F∈L, 使得对任意的 x, 我们都有 F(x)−F(x+a)=0. |
B13) | 假设 λ=1. 在 (⋆) 中取函数 f(x)=cos(x). 证明, 如果 cos(a)=1, 那么存在 F∈L 是 (⋆) 的解. 进一步阐述这个解是否唯一? |
B14) | 假设 λ=1. 在 (⋆) 中取函数 f(x)=cos(x). 证明, 如果 a=2π, 那么我们不能在 L 中找到 F, 使得 F 是 (⋆) 的解. |
B15) | 假设 λ=−1. 证明, 存在非零的函数 F∈L, 使得对任意的 x, 我们都有 F(x)+F(x+a)=0. |
B16) | 假设 λ=−1, a=1, f∈L, f 是递减的并且 x→+∞limf(x)=0, f 可微并且 f′ 是递增的. 证明, 存在 F∈L, 解如下方程: F(x)+F(x+1)=f(x), x∈R.进一步, 如果我们要求 F∈L 并且 x→+∞limF(x)=0, 那么这样的解是存在唯一的. |