习题课: 球极投影
隐函数定理的习题
第三次作业 B3)
假设 是光滑映射, 是 的不动点, 即 . 假设 不是 在 处的微分的特征值.
• | 证明, 是一个孤立的不动点, 即存在开集 , 使得 , 在 有且仅有 为其不动点. |
• | 任意给定 . 对任意的 , 我们定义映射证明, 存在 , 存在 在 的开邻域 以及 的映射使得对任意的 , 在 中恰好有一个不动点 . |
第三次作业 D2)
(根对系数的光滑依赖性) 考虑实系数多项式 . 如果对 , 恰好有 个两两不同的实根 . 证明, 存在 的开邻域 和 上的光滑函数 , 使得对任意的 , 我们有并且
子流形
子流形的切空间的线性结构 (参考第六课讲义的脚注)
假设 是子流形, 我们想要说明 是线性空间. 根据定义, 存在开集 , , 存在开集 以及微分同胚, 使得 是微分同胚. 所以, 我们有对于 这种情况, 我们课上已经计算了 处的切空间, 这是一个 的 维线性子空间. 另外, 根据切空间的微分不变性, 我们有由于 是线性同构, 所以, 作为一个线性子空间的逆像还是线性子空间.
你是否能说明, 作为线性空间结构不依赖于开集 , , 开集 以及微分同胚 的选取?
球极投影 (未完待续)
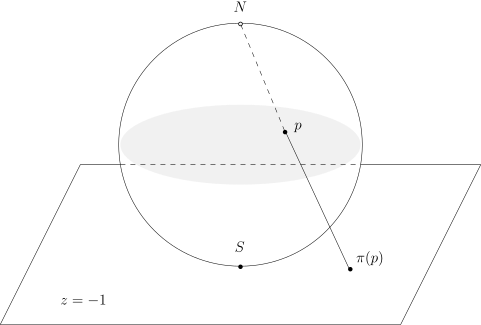
我们考虑 (用坐标 ) 中的单位球面 , 令 为其北极, 为其南极. 我们知道, 就是平面 , 我们用 来表示这个平面. 对任意的 , , 我们考虑从 到 的连线, 它与 恰好相交于一个点 . 于是, 我们有映射这个映射被称作是从北极到南极切平面的球极投影.
• | 证明, 中的任意的平面 (由某个线性函数 的零点定义) 与 的交是圆 (如果非空的话, 半径可以是 ) . 我们称它们为球面上的圆. |
• | 证明, 是子流形之间的光滑映射并且给出了 与 之间的微分同胚. |
• | 证明, 对任意的 , 试计算微分 . |
• | 证明, 这个映射是所谓的共形映射, 即它保持角度: 对于任意的 , 我们有 (用 中的内积) |
• | 把 上不过北极的圆映成圆, 把过北极的圆映射成直线并且 上的每个圆和直线都可以这么得到. |
• | 如果把 换成其他点 处的切空间, 上面的结论是否成立? |