用户: Noneghost/几何与对称

本文来源于作者 2018 年在清华大学为首届丘成桐英才班开设的教改课程《几何与对称》的部分内容 [链接], 通过几何直观和棋盘游戏实例来解释 “群” 这个重要数学概念的一些基本思想和应用方法. 我们把部分内容作为附录放在这份讲义里, 希望能帮助读者更好地了解我们在定义行列式时使用的置换变换, 并初步了解群这个概念.

引言

大学数学系里通常有一门基础课称为 “抽象代数”, 主要内容是群、环、域等这些现代代数学中的基本概念和方法. 读书的时候感觉这些概念初学起来的确很 “抽象”, 就像这门课的名称一样. 随着不断学习和积累, 逐渐发现这些概念其实非常直观, 朋友们也经常笑谈到这门课应该被教为 “非抽象代数”. 本文通过一个具体的数字游戏来聊聊非抽象代数.

我们探讨的这个经典例子称为数字推盘问题, 玩法类似于华容道. 考虑一个 $4 \times 4$ 的方形棋盘以及标记 $1 - 15$ 的数字方块. 游戏者每次移动一个数字方块到相邻空白格, 例如

问题: 是否可以由下图左还原到下图右的原始状态?

我们将围绕如何解决这个经典问题来解释 “群” 这个基本数学概念.

几何变换与对称性

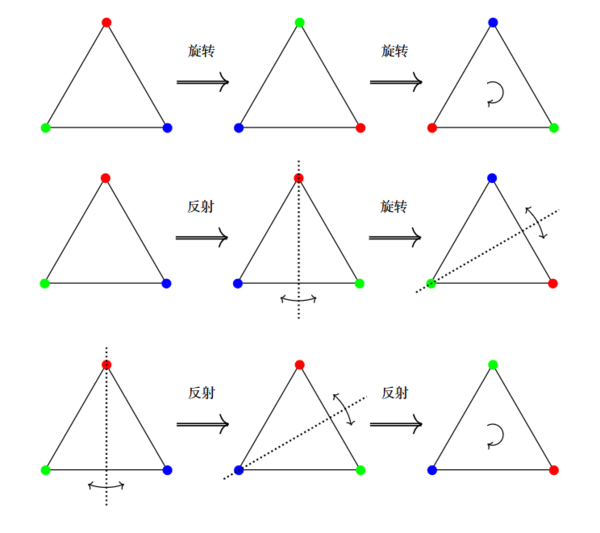
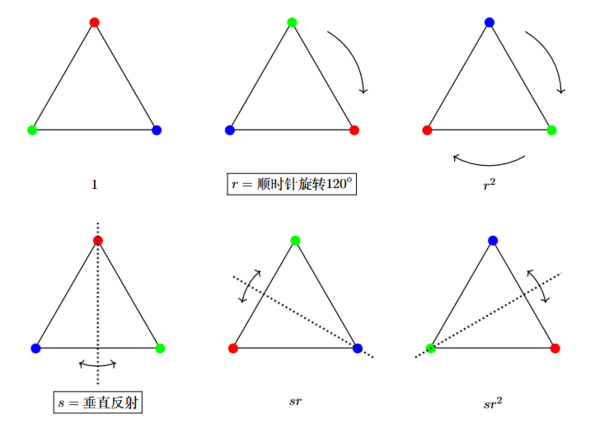
具有几何对称的物体通常都有强烈美感和丰富结构, “群” 即刻画如此. 考虑等边三角形

这个图形具有很强的几何对称性: 我们可以通过如下的几何变换把三角形变换到它自己

我们总共得到如下 6 个对称变换

观察到这些几何变换满足如下两个重要性质:

1. 对称变换的复合还是对称变换

2. 对称变换可以由逆变换来还原

群的概念

几何对称变换的这些性质构成的数学对象称为 “群”.

抽象定义而言, 一个群由一个集合 $G$ 和满足结合律的二元运算 $∙ : G \times G \to G$ (称为群 $G$ 中的乘积) 组成, 满足

•	单位元: 存在单位元 $1_{G}$ , 使得: $1_{G} ∙ g = g ∙ 1_{G} = g$
•	可逆性: 对任一元素 $g$ , 存在逆元 $g^{- 1}$ 使得: $g ∙ g^{- 1} = g^{- 1} ∙ g = 1_{G}$

例如:

1.

$G = R - {0}$ , $∙$ 为实数的乘法 $a ∙ b := ab$

单位元= $1$ , $a$ 的逆元是 $\frac{1}{a}$

2.

$G = Z$ , $∙$ 为整数的加法 $m ∙ n := m + n$

单位元= $0$ , $m$ 的逆元是 $- m$

上述例子中 $∙$ 是交换的, 即满足: $a ∙ b = b ∙ a$ . 乘积满足交换性质的群称为阿贝尔群.

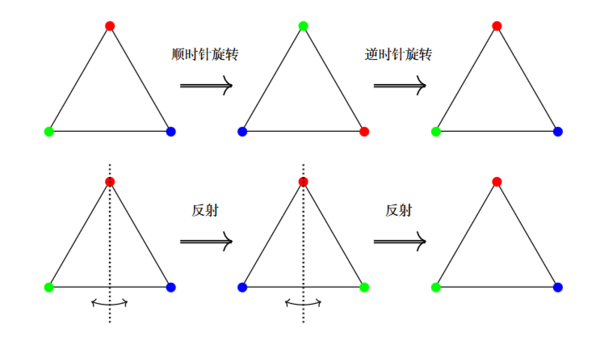
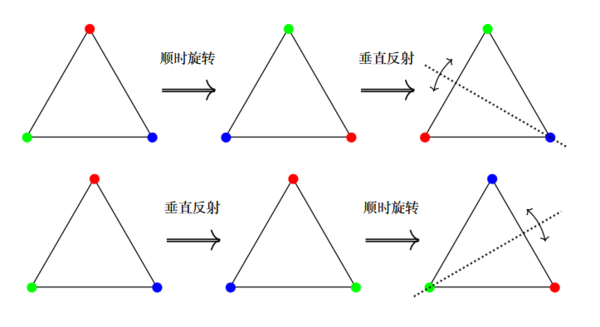
例如: 如下 6 个几何变换组合成一个群 (称为二面体群 $D_{3}$ )

$D_{3}$ 是非阿贝尔群: 旋转和反射不交换!

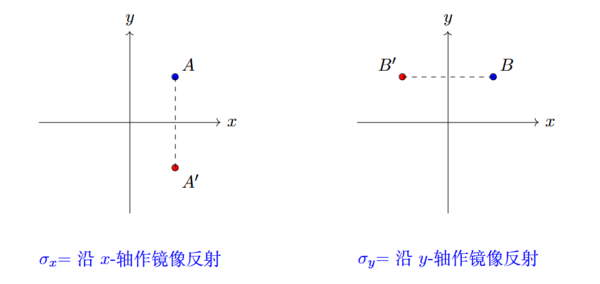
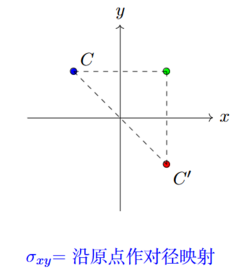
例如: 考虑平面上的几何变换

我们得到如下的变换复合关系: $σ_{x} \cdot σ_{x} = σ_{y} \cdot σ_{y} = σ_{x y} \cdot σ_{x y} = 恒等变换 σ_{x} \cdot σ_{y} = σ_{y} \cdot σ_{x} = σ_{x y} σ_{y} \cdot σ_{x y} = σ_{x y} \cdot σ_{y} = σ_{x} σ_{x y} \cdot σ_{x} = σ_{x} \cdot σ_{x y} = σ_{y}$ 这些变换 ${1, σ_{x}, σ_{y}, σ_{x y}}$ 构成一个阿贝尔群, 称为 Klein 四元群. 特别的我们有 $σ_{x} \cdot σ_{y} \cdot σ_{x y} = 恒等变换（单位元 1 ）$

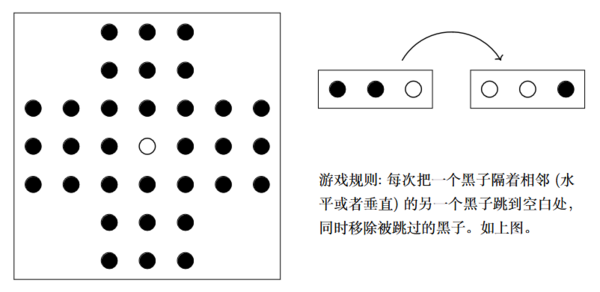
一个古老的游戏 (Peg Solitaire)

群的结构表现为变换. 在实际运用中, 一个重要的思想是在一系列丰富的变换中找到不变的对象. 作为一个例子, 我们考虑一个古老的游戏:

问题: 是否可以使得棋盘上最后只剩下一个黑子? 如果可以, 这个黑子落在哪里?

通过实践很容易发现第一问的答案是肯定的, 我们用群论方法来分析第二问. 把 Klein 四元群元素如下标记到棋盘中

这个标记方法使得直线上任意三个相邻元素的乘积都是恒等变换单位元 1.

设 $C$ 是棋盘上的一个黑子分布. 定义 $C$ 的权为

$[C] =$ 所有的黑子位置上的 Klein 四元群元素相乘

上图右的权= $σ_{x} \cdot σ_{x y} \cdot σ_{x} \cdot σ_{x} = σ_{y}$

观察到: 如果 $C$ 走一步得到 $C^{'}$ , 则 $[C] = [C^{'}]$ 具有相同的权. 因此 “权” 为游戏过程中的一个不变量.

容易计算初始黑子分布的权为 $σ_{y}$

因此最后一个黑子只可能落在标记为 $σ_{y}$ 的位置.

黑子最后不可能落在如下右图绿点的位置 (权为 $σ_{x y}$ ). 由左右对称性, 可以排除最后一个黑子落在如下左图的可能性 (否则可以采取左右镜像的走法使得最后落在右图绿点) .

类似对称性分析, 我们可以共排除如下 6 种可能

最后一个黑子只能落在如下图中的某个位置

实际上这 5 种可能性都可以达到, 而且我们总可以使得最后一个黑子落在正中间. 假如最后一个黑子落在如下左图的位置, 则上一步如中间图. 可以改变走法使得最后一个黑子落在右图的位置. 这样我们就完整地解决了这个问题.

置换群

集合 ${1, 2, \dots, n}$ 到自己的一个一一映射称为一个 $n$ 元置换. 例如: 如下映射 $σ$ 是一个 5 元置换

$σ : 1, 2, 3, 4, 5 \to 3, 1, 5, 2, 4$

两个置换的复合也是置换. 所有 $n$ 元置换构成一个群 (称置换群), 记为 $S_{n}$ .

一个 $n$ 元置换 $σ$ 可以记为

$σ = [1 i_{1} 2 i_{2} \dots \dots n i_{n}]$

$σ$ 表示将 $1$ 变成 $i_{1}$ , $2$ 变成 $i_{2}$ , ..., $n$ 变成 $i_{n}$ . 例如

$σ = [1321354254]$

表示置换 $σ : 1, 2, 3, 4, 5 \to 3, 1, 5, 2, 4$ . 乘积 $α β$ 表示先作用 $β$ 置换, 再作用 $α$ 置换. 例如 $[122133] [112332] = [122331]$

如果置换 $σ$ 把其中 $k$ 个元素映射为

$σ : i_{1}, i_{2}, i_{3}, \dots, i_{k} \to i_{2}, i_{3}, \dots, i_{k}, i_{1}$

而把其他元素映射到自己, 我们称 $σ$ 是一个长度为 $k$ 的轮换, 并把 $σ$ 简化标记为 $σ = (i_{1} i_{2} \dots i_{k})$ 例如: $σ = [1123354452] = (235)$

任意一个置换总可以表示为一些轮换的乘积, 例如 $[112436425365] = (1) (24) (365) = (24) (365)$ 其中 $(1)$ 表示的是恒等置换, 可以省略不记.

交错群 (偶置换群)

长度为 2 的轮换 $(i j)$ 称为一个对换. 例如 $σ = [1125334452] = (25)$ 每个轮换均可以表示为一些对换的乘积, 但是这种表达方式不唯一. 例如 $(123) = (13) (12) = (12) (23)$ $[122331] = [122133] [112332]$

由于每个置换总可以表示为一些轮换的乘积, 因此每个置换也总可以表示成一些对换的乘积. 虽然表达法不唯一, 但是容易发现不同表达法里包含的对换个数的奇偶性是确定不变的, 称为该置换的奇偶性. 例如: 长度 $k$ 的轮换可以写成 $k - 1$ 个对换相乘

$(123 \dots k) = (1 k) (1 k - 1) \dots (13) (12)$

因此我们知道奇长度的轮换是偶置换, 偶长度的轮换是奇置换. 例如 $奇置换 : 偶置换 : (23), (1347) = (17) (14) (13) (123) = (13) (12), (43216)$

置换的复合满足 $奇置换 \times 奇置换 \to 偶置换奇置换 \times 偶置换 \to 奇置换偶置换 \times 偶置换 \to 偶置换$

因此 $S_{n}$ 中所有偶置换构成一个群 (称为交错群) , 记为 $A_{n}$ .

数字推盘问题的解-必要条件

问题: 是否可以由图左还原到图右原始位置?

上图左对应于一个置换 $σ = [1152231412586576811941091110127133141415131616]$ 这里我们把空白标记为 $16$ .

如果棋盘的布置可以从原始的位置 (上图右) 移动得到, 它对应的置换 $σ$ 应该满足什么性质? 移动过程可以通过记录空白位置的走动来标志

每个移动为 $S_{16}$ 中的一个对换 (空白标志为 $16$ ). 如果要求将空白移回到出发点, 则

往上走步数＝往下走步数, 往左走步数＝往右走步数

总共要移动偶数步! 因此数字推盘问题可解的一个必要条件是

推盘对应的数字置换是偶置换

回到这节开始的问题, 推盘对应的置换 $σ = [1152231412586576811941091110127133141415131616] = (115133) (412765811109)$ 是奇置换, 因此我们知道它对应的数字推盘不可能还原到原始状态.

进一步, 我们可以考虑

问题: 如果数字推盘对应的数字置换是偶置换, 是否一定可以还原?

答案是肯定的. 为了证明这个结论, 我们需要引入群的生成元的概念.

群的生成元

群 $G$ 的一组元素称为生成元, 如果 $G$ 中每个元素都可以通过这组元素反复相乘得到.

例如: Klein 群 $K = {1, a, b, c}$ $a ∙ b = c a^{2} = 1 b ∙ c = a b^{2} = 1 c ∙ a = b c^{2} = 1$

•	${a, b}$ 是一组生成元. 比如 $1$ 可以由 $a ∙ a$ 得到, $c$ 可以由 $a ∙ b$ 得到.
•	${b, c}$ 也是一组生成元. 因此生成元的选法并不唯一.

例如: 二面体群 $D_{3}$ 的一组生成元是 ${r, s}$ , 它们满足 $r^{3} = 1, s^{2} = 1, sr = r^{2} s$

例如: 置换群 $S_{n}$ 可以由如下对换生成 $(12), (13), \dots, (1 n)$ 比如任意的置换 $(i j)$ 可以写成 $(i j) = (1 j) (1 i) (1 j)$ 由此可以生成所有的置换. 类似的, 给定其他一个数比如 $3$ , 如下对换 $(31), (32), (34) \dots, (3 n)$ 也构成 $S_{n}$ 的一组生成元.

例如: 交错群 $A_{n}$ (即 $S_{n}$ 中的偶置换) 的一组生成元是 $(123), (124), \dots, (12 n)$ 类似的, 给定其他两个数比如 2, 4, 如下轮换 $(241), (243), (245) \dots, (24 n)$ 也构成 $A_{n}$ 的一组生成元. 读者可以尝试着证明这个结论.

数字推盘问题的解-充分条件

我们下面来分析求解数字推盘问题的充分条件. 首先我们考虑两个特殊的移动.

第一个移动为:

通过如上移动, 我们知道如下置换是可以还原的 $τ = (111215)$

第二个移动为:

通过如上移动, 我们知道如下置换是可以还原的 $ρ = [152137435962768491310151111121213141410158] = (15913141015843762)$

观察到: 如果置换 $σ_{1}, σ_{2}$ 可以还原, 那么

•	$σ_{1} σ_{2}$ 可以还原: 通过复合操作实现
•	$σ_{1}^{- 1}$ 可以还原: 通过逆向操作实现

换言之, 所有可以还原的置换构成了一个群.

通过上述两个移动, 我们知道如下两个置换是可以还原的 $τ = (111215), ρ = (15913141015843762)$ 因此由它们及其逆元复合生成的置换均可还原. 直接计算发现 $τ, ρ τ ρ^{- 1}, ρ^{2} τ ρ^{- 2}, \dots, ρ^{12} τ ρ^{- 12}$ 恰好构成集合 (顺序不一致) $(11121), \dots (111210), (111213), (111214), (111215)$ 因此这些置换均可以被还原. 由上述讨论, 我们知道元素 $(11121), \dots (111210), (111213), (111214), (111215)$ 生成所有的 15 元的偶置换. 因此任意一个对应于偶置换的数字推盘均可以还原! 总结上述讨论, 我们通过置换群的结构证明了如下结论:

定理. 数字推盘可以被还原到初始状态当且仅当其对应的数字置换是偶置换.

例如对于上面这个问题, 它对应的置换 $σ = = [192431412510657681192101511812713314141513] (1924127651015133) (811)$ 是偶置换, 因此我们知道它一定可以被还原.

名字空间

视图