用户: Jin1/纤维丛的同伦群计算

本文参考 A.Hatcher, Algebraic Topology 4.2 节, Fiber Bundles.

定义 0.1 (同伦提升性质). 称一个映射 $p:E\to B$ 具有关于 $X$ 的同伦提升性质, 是指, 只要有一个同伦 $g_t:X\to B$ 且 $g_0$ 有提升 ${\tilde{g}}_0:X\to E$, 那么整个同伦就有提升 ${\tilde{g}}_t:X\to E$.

定义 0.2 (提升扩张性质). 称一个映射 $p:E\to B$ 具有关于有序对 $(Z,A)$ 的提升扩张性质, 是指, 对任意映射 $f:Z\to B$, 只要给定 $A$ 上的提升 $\tilde{f}:A\to E$, 就有 $Z$ 上的提升 $\tilde{f}:Z\to E$.

关于 $X$ 的同伦提升性质就是关于 $(X\times I,X\times \{0\})$ 的提升扩张性质.

同伦提升性质还有一个 “相对” 的版本.

定义 0.3. 称一个映射 $p:E\to B$ 具有关于有序对 $(X,A)$ 的相对同伦提升性质, 是指, 只要有一个同伦 $g_t:X\to B$ 且 $g_0$ 有提升 ${\tilde{g}}_0:X\to E$ 且给定了 $A$ 上的提升 ${\tilde{g}}_t:A\to E$, 那么就有提升 ${\tilde{g}}_t:X\to E$.

换句话说, 关于有序对 $(X,A)$ 的相对同伦提升性质就是 $(X\times I,X\times \{0\}\cup A\times I)$ 的提升扩张性质.

定义 0.4 (纤维化). 称一个映射 $p:E\to B$ 是纤维化是指它对任意空间 $X$ 都有同伦提升性质.

例 0.5. 投影映射 $p:B\times F\to B$ 是纤维化.

纤维化可以看作同伦意义下的覆盖空间.

定理 0.6. 假设 $p:E\to B$ 对于所有 $I^n(n\ge 0)$ 有同伦提升性质. 选取 $b_0\in B$ 与 $x_0\in F=p^{-1}(b_0)$, 则有同构$$p_{\ast }:{\pi }_n(E,F,x_0)\to {\pi }_n(B,b_0)(n\ge 1).$$从而在 $B$ 道路连通时就有长正合列$$\begin{array}{rl}\cdots \to {\pi }_n(F,x_0)\to {\pi }_n(E,x_0)& \stackrel{p_{\ast }}{\to }{\pi }_n(B,b_0)\to {\pi }_{n-1}(F,x_0)\to \cdots \\ \to {\pi }_0(F,x_0)& \to {\pi }_0(E,x_0)\to 0.\end{array}$$

注意到, 关于 $I^n$ 的同伦提升性质等同于关于 $(I^n,\partial I^n)$ 的同伦提升性质. 这是因为有序对 $(I^n\times I,I^n\times \{0\})$ 同胚于 $(I^n\times I,I^n\times \{0\}\cup (\partial I^n)\times I)$. 具有这个性质的映射有时称作 Serre 纤维化.

证明. 先证明 $p_{\ast }$ 满. 对于 ${\pi }_n(B,b_0)$ 的一个元素, 将其表示为$$f:(I^n,\partial I^n)\to (B,b_0).$$

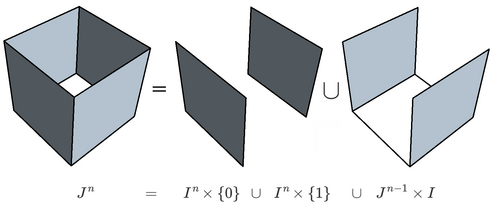
定义 $J^{n-1}=\overline{\partial I^n-I^{n-1}}$, 即 $I^n$ 除了一个面以外其余的面. 右图是 $J^2$.

注意到$$J^{n-1}\simeq I^{n-1}\times \{0\}\cup (\partial I^{n-1})\times I,$$故关于 $(I^{n-1},\partial I^{n-1})$ 的同伦提升性质即关于 $(I^n,J^{n-1})$ 的提升扩张性质.

如下图, 常值映射 $x_0$ 是常值映射 $b_0$ 的提升, 因此, 由关于 $(I^n,J^{n-1})$ 的提升扩张性质, 这个提升可扩张到 $I^n$ 上, 得到其中 $\tilde{f}$ 表示了 ${\pi }_n(E,F,x_0)$ 的一个元素.

再证明 $p_{\ast }$ 是单射. 设 ${\tilde{f}}_0,{\tilde{f}}_1:(I^n,\partial I^n,J^{n-1})\to (E,F,x_0)$ 满足 $p_{\ast }([{\tilde{f}}_0])=p_{\ast }([{\tilde{f}}_1])$. 那么, 可取 $p{\tilde{f}}_0$ 到 $p{\tilde{f}}_1$ 的同伦$$G:(I^n\times I,(\partial I^n)\times I)\to (B,b_0).$$

注意到

故

•	${\tilde{f}}_0:I^n\times \{0\}\to E,$
•	${\tilde{f}}_1:I^n\times \{1\}\to E,$
•	$x_0:J^{n-1}\times I\to E$

共同给出了 $G$ 在 $J^n$ 上的提升. 由关于 $(I^n\times I,J_n)$ 的提升扩张性质, 存在提升 $\tilde{G}:I^n\times I\to E$, 即 ${\tilde{f}}_0$ 与 ${\tilde{f}}_1$ 同伦. 这证明了 $p_{\ast }$ 是单射.

最后, 假设 $B$ 道路连通. 回忆, 存在长正合列$$\begin{array}{rl}\cdots \to {\pi }_n(F,x_0)\to {\pi }_n(E,x_0)& \to {\pi }_n(E,F,x_0)\stackrel{\partial }{\to }{\pi }_{n-1}(F,x_0)\to \cdots \\ \to {\pi }_0(F,x_0)& \to {\pi }_0(E,x_0)\to 0.\end{array}$$使用上面证明的同构将 ${\pi }_n(E,F,x_0)$ 换成 ${\pi }_n(B,b_0)$. 长正合列末端的满射 ${\pi }_0(F,x_0)\to {\pi }_0(E,x_0)$ 是由于 $B$ 道路连通, 从而对任意 $x\in E$, 将 $p(x)$ 到 $b_0$ 的道路提升, 就得到了 $x$ 到 $F$ 的道路.

$\square$

术语翻译

纤维化 • 英文 fibration

同伦提升性质 • 英文 homotopy lifting property

提升扩张性质 • 英文 lift extension property

相对同伦提升性质 • 英文 relative homotopy lifting property