用户: ACR/Dedekind 整环

为了弥补代数整数环不再具有唯一分解性质这一缺陷, Kummer 引入了理想数这一概念, 并证明了理想数具有的唯一分解性质. 随后, “理想” 这一概念被推广到一般的环上.

我们关心的问题是: 对什么样的整环 $R$, $R$ 中的非零理想可以被唯一分解成素理想的乘积. 这就是我们接下来要考虑的 Dedekind 整环:

定义. 称整环 $R$ 是一个 Dedekind 整环, 如果有如下条件:

$(1)$ $R$ 是 Noether 环;

$(2)$ $R$ 是整闭的, 即若 $x\in \mathrm{Frac}(R)$ 满足方程$$x^n+a_{n-1}{x}^{n-1}+\cdots +a_0=0,a_i\in R,$$则一定有 $x\in R$.

$(3)$ $R$ 中的每一个非零素理想都是极大理想. 也就是说, $R$ 的维数是 $1$.

性质. 如下条件等价:

$(1)$ $R$ 是 Dedekind 整环;

$(2)$ $R$ 是 Noether 整环, 且对每个非零素理想 $\mathfrak{p}$, $R_{\mathfrak{p}}$ 是离散赋值环.

$(3)$ $R$ 的每一个非零分式理想 ¹ 都是可逆的.

证明. $(1)\Rightarrow (2)$. 根据离散赋值环的性质, 我们只需要证明对每个素理想 $\mathfrak{p}$, $R_{\mathfrak{p}}$ 是 Noether 且整闭的, 同时有且仅有一个非零素理想.

每一个 $R_{\mathfrak{p}}$ 中理想形如 ${\mathfrak{a}}_{\mathfrak{p}}$, 其中 $\mathfrak{a}$ 是 $R$ 中理想. 由于 $R$ 是 Noether 的, $\mathfrak{a}$ 被 $R$ 中有限个元素生成. 这些元素在 $R_{\mathfrak{p}}$ 中生成 ${\mathfrak{a}}_{\mathfrak{p}}$, 因此 $R_{\mathfrak{p}}$ 也是 Noether 的.

设 $K$ 是 $R$ 的分式域, 那么 $K$ 同样是 $R_{\mathfrak{p}}$ 的分式域. 由于 $R$ 在 $K$ 中整闭, $R_{\mathfrak{p}}$ 在 $K_{\mathfrak{p}}=K$ 中同样整闭.

$R_{\mathfrak{p}}$ 的素理想一一对应于 $R$ 中包含在 $\mathfrak{p}$ 里的素理想, 因而只有 $0$ 和 $\mathfrak{p}{R}_{\mathfrak{p}}$. 从而 $\mathfrak{p}{R}_{\mathfrak{p}}$ 是其唯一的非零素理想. 故 $R_{\mathfrak{p}}$ 是离散赋值环.

$(2)\Rightarrow (3)$. 我们只要证对任意非零分式理想 $I$, 都有 $I{I}^{-1}=R$ 成立. 由于 $I{I}^{-1}\subset R$, 如果 $I{I}^{-1}\ne R$, 其一定包含在某个非零素理想 $\mathfrak{p}$ 中. 换言之, $(I{I}^{-1}{)}_{\mathfrak{p}}=I_{\mathfrak{p}}(I^{-1}{)}_{\mathfrak{p}}\subset \mathfrak{p}{R}_{\mathfrak{p}}.$

由 $R$ 是 Noether 环, $I$ 由有限个元素 $a_1,\dots ,a_n\in K$ 的 $R$ 系数线性组合生成. 又由于 $R_{\mathfrak{p}}$ 是离散赋值环, 存在 $x\in R_{\mathfrak{p}}$ 使得 $I_{\mathfrak{p}}=x{R}_{\mathfrak{p}}$. 我们以 $v_{\mathfrak{p}}$ 表示 $R_{\mathfrak{p}}$ 上的离散赋值.

一方面, 对每个 $a_i$, 都有 $b_i\subset R-\mathfrak{p}$, 使得 $a_i{b}_i\in xR$. 从而 $v_{\mathfrak{p}}(x)\le v_{\mathfrak{p}}(a_i)$. 另一方面, $x{R}_{\mathfrak{p}}$ 由 $a_1,\dots ,a_n$ 以 $R_{\mathfrak{p}}$ 为系数的线性组合张成. 因此 $x=\sum a_i{c}_i$, 其中 $c_i\in R_{\mathfrak{p}}$. 强三角不等式表明 $v_{\mathfrak{p}}(x)\ge \min v_{\mathfrak{p}}(a_i)$, 因此 $v_{\mathfrak{p}}(x)=\min v_{\mathfrak{p}}(a_i)$. 不妨设 $v_{\mathfrak{p}}(x)=v_{\mathfrak{p}}(a_1)$.

由于 $v_{\mathfrak{p}}(a_1^{-1}{a}_i)=v_{\mathfrak{p}}(a_i)-v_{\mathfrak{p}}(a_1)\ge 0$, $a_1^{-1}{a}_i\in R_{\mathfrak{p}}$. 故存在 $d_i\in R-\mathfrak{p}$, 使得 $a_1^{-1}{a}_i{d}_i\in R$. 若令 $d=\prod _i{d}_i\in R-\mathfrak{p}$, 由 $d{a}_1^{-1}{a}_i\in R$ 知 $d{a}_1^{-1}\in I^{-1}$, 因此 $a_1^{-1}\in (I^{-1}{)}_{\mathfrak{p}}$. 故 $1=a_1{a}_1^{-1}\in I_{\mathfrak{p}}(I^{-1}{)}_{\mathfrak{p}}=(I{I}^{-1}{)}_{\mathfrak{p}}$. 这与我们的假设矛盾.

$(3)\Rightarrow (1)$. 条件相当于说, 全体非零分式理想在乘法下构成群.

如果分式理想 $I$ 是可逆的, 那么可以取 $a_1,\dots ,a_n\in I$ 以及 $b_1,\dots ,b_n\in I^{-1}$, 使得$$\sum _{i=1}^n{a}_i{b}_i=1.$$

首先, 对每一个 $x\in I$, 我们可以将其写成 $1\cdot x=\sum a_i{b}_{i}x$. 按照定义, $b_{i}x$ 落在 $R$ 中. 从而 $I$ 可以由 $a_1,\dots ,a_n\in I$ 以 $R$ 系数线性组合生成, 因此是有限生成的. 这表明 $R$ 是 Noether 的.

仍以 $K$ 记 $R$ 的分式域. 假设 $x\in K$ 是 $R$ 上的整元素, $S=R[x]$ 既是分式理想又是环. 因此由 $S$ 中两个元素的乘积生成的分式理想恰好是 $S$, 也即 $S^2=S$. 按假定, $S$ 是可逆的. 因而我们有$$S=SR=S(S{S}^{-1})=(SS)S^{-1}=S{S}^{-1}=R.$$

设 $I$ 是一个非零的素理想, 那么存在极大理想 $\mathfrak{p}\supset I$. 同时 ${\mathfrak{p}}^{-1}I\subset {\mathfrak{p}}^{-1}\mathfrak{p}=R\subset {\mathfrak{p}}^{-1}R={\mathfrak{p}}^{-1}$. 这说明 ${\mathfrak{p}}^{-1}I$ 是 $R$ 中的一个理想. 由于 $I=\mathfrak{p}({\mathfrak{p}}^{-1}I)$, 且 $I$ 是素理想, 根据素理想的性质, 或者 $\mathfrak{p}\subset I$, 或者 ${\mathfrak{p}}^{-1}I\subset I$. 前者表明 $I=\mathfrak{p}$ 是极大理想, 而后者给出$$\mathfrak{p}({\mathfrak{p}}^{-1}I)I^{-1}=R\subset \mathfrak{p}I{I}^{-1}=\mathfrak{p}.$$与我们的假设矛盾.

$\square$

接下来, 我们假设 $R$ 是一个 Dedekind 整环, $K$ 是其分式域, 对素理想 $\mathfrak{p}$, 记 $K$ 上与 $R_{\mathfrak{p}}$ 关联的离散赋值记为 $v_{\mathfrak{p}}$.

推论. 对 $K$ 上每一个满足 $|R|\le 1$ 的非平凡离散乘性赋值 $|\cdot |$, 都存在一个非零素理想 $\mathfrak{p}$ 及正实数 $0<\rho <1$, 使得$$|x|={\rho }^{v_{\mathfrak{p}}(x)},\forall x\in K.$$

证明. 我们知道, $|R|\le 1$ 可以推出强三角不等式.

离散乘性赋值由 $|x|={\rho }^{v(x)}$ 给出, 其中 $0<\rho <1$, $v$ 是一个离散赋值.

我们令 $\mathfrak{p}=\{x\in R\mid |x|<1\}$. 我们断言这是一个 $R$ 中的素理想:

如果对每一个 $x\in R-\{0\}$, 都有 $|x|=1$, 由于 $K$ 是分式域, 这推出 $|\cdot |$ 是平凡的. 同我们的假定矛盾, 于是一定有某个 $s\in \mathfrak{p},s\ne 0$.

若 $|x|,|y|<1$, 则 $|x+y|\le \max \{|x|,|y|\}<1$.

若 $a\in R$, $|ax|=|a|\cdot |x|\le |x|<1$.

若 $xy\in \mathfrak{p}$, 则 $|x|\cdot |y|<1$ 可推出 $|x|<1$ 或 $|y|<1$. 因此 $x\in \mathfrak{p}$ 或 $y\in \mathfrak{p}$.

$|1|=1$. 因此 $\mathfrak{p}\ne R$. 故 $\mathfrak{p}$ 是 $R$ 中素理想.

前面的性质给出 $R_{\mathfrak{p}}$ 是离散赋值环. 我们还需证明: $R_{\mathfrak{p}}$ 恰好是 $v$ 对应的那个离散赋值环 $R_v$, 从而 $v_{\mathfrak{p}}$ 正是 $v$.

设 $x\in R_v-R_{\mathfrak{p}}$, 则 $x^{-1}\in R_{\mathfrak{p}}\subset R_v$. 从而 $x$ 是 $R_v$ 中的单位, 也即 $|x^{-1}|=1$. 这说明 $x^{-1}\in R_{\mathfrak{p}}$ 不在其极大理想 $\mathfrak{p}{R}_{\mathfrak{p}}$ 内, 因而 $x^{-1}$ 也是 $R_{\mathfrak{p}}$ 中的单位, 从而 $x\in R_{\mathfrak{p}}$, 与假定矛盾. 于是命题得证.

$\square$

类比整数 (有理数) 的情形, 我们希望对理想 (分式理想) 也定义赋值 $v_{\mathfrak{p}}(I)$. 现设有子集 $E\subset K$, 我们定义 $v_{\mathfrak{p}}(E)=\underset{x\in E}{\inf }{v}_{\mathfrak{p}}(E).$ 注意 $v_{\mathfrak{p}}(E)$ 可能等于 $\pm \infty$. 不难发现如下的性质:

性质. $(1)$ $E\subset F\Rightarrow v_{\mathfrak{p}}(E)\ge v_{\mathfrak{p}}(F)$.

$(2)$ 设 $E$ 非空, $v_{\mathfrak{p}}(E)=v_{\mathfrak{p}}(RE)=v_{\mathfrak{p}}(R_{\mathfrak{p}}E)$, 其中 $RE,R_{\mathfrak{p}}E$ 分别是 $E$ 在 $K$ 中生成的 $R$ 子模和 $R_{\mathfrak{p}}$ 子模.

$(3)$ 对 $K$ 中的非零 $R$ 分式理想 $I$, $v_{\mathfrak{p}}(I)$ 总是有限的.

$(4)$ 设 $I_1,I_2$ 是 $K$ 中的非零 $R$ (或者 $R_{\mathfrak{p}}$) 分式理想. 则 $v_{\mathfrak{p}}(I_1{I}_2)=v_{\mathfrak{p}}(I_1)v_{\mathfrak{p}}(I_2)$.

$(5)$ 设 ${\mathfrak{p}}^{\prime }$ 是 $R$ 中一个不同于 $\mathfrak{p}$ 的素理想, 则 $v_{\mathfrak{p}}({\mathfrak{p}}^{\prime })=0,v_{\mathfrak{p}}(\mathfrak{p})=1$.

$(6)$ 设 $I_1,I_2$ 是 $R$ 分式理想, 那么$$v_{\mathfrak{p}}(I_1+I_2)=\min (v_{\mathfrak{p}}(I_1),v_{\mathfrak{p}}(I_2));$$$$v_{\mathfrak{p}}(I_1\cap I_2)=\max (v_{\mathfrak{p}}(I_1),v_{\mathfrak{p}}(I_2)).$$

证明. $(1)$ 是明显的.

$(2)$ 由包含关系得到 $v_{\mathfrak{p}}(E)\ge v_{\mathfrak{p}}(RE)$, $v_{\mathfrak{p}}(E)\ge v_{\mathfrak{p}}(R_{\mathfrak{p}}E)$. 对任意 $e_1,\dots ,e_n\in E$, $x_1,\dots ,x_n\in R$ (相应地, $R_{\mathfrak{p}}$) , 总有$$v_{\mathfrak{p}}(e_1{x}_1+\cdots +e_n{x}_n)\ge \inf v_{\mathfrak{p}}(e_i{x}_i)\ge \inf v_{\mathfrak{p}}(e_i)\ge v_{\mathfrak{p}}(E),$$于是反向的不等式也成立, 即 $v_{\mathfrak{p}}(RE)=v_{\mathfrak{p}}(R_{\mathfrak{p}}E)=v_{\mathfrak{p}}(E)$.

$(3)$ 存在 $a\in R-\{0\}$, $aI\subset R$. 于是对 $I$ 中任意非零元素 $x$, $v_{\mathfrak{p}}(ax)\ge 0\Rightarrow +\infty >v_{\mathfrak{p}}(x)\ge -v_{\mathfrak{p}}(a)$.

$(4)$ $I_1{I}_2$ 由形如 $x_1{x}_2(x_j\in I_j,j=1,2)$ 的元素的 $R$ 系数 (相应地, $R_{\mathfrak{p}}$ 系数) 线性组合构成, 故$$v_{\mathfrak{p}}(I_1{I}_2)=\underset{x_j\in I_j,j=1,2}{\inf }{v}_{\mathfrak{p}}(x_1{x}_2)=v_{\mathfrak{p}}(I_1)v_{\mathfrak{p}}(I_2).$$

$(5)$ $v_{\mathfrak{p}}({\mathfrak{p}}^{\prime }{R}_{\mathfrak{p}})=v_{\mathfrak{p}}(R_{\mathfrak{p}})=0$, $v_{\mathfrak{p}}(\mathfrak{p})=v_{\mathfrak{p}}(\mathfrak{p}{R}_{\mathfrak{p}})=1$.

$(6)$ 注意到 $(I_1+I_2{)}_{\mathfrak{p}}=(I_1{)}_{\mathfrak{p}}+(I_2{)}_{\mathfrak{p}},(I_1\cap I_2{)}_{\mathfrak{p}}=(I_1{)}_{\mathfrak{p}}\cap (I_2{)}_{\mathfrak{p}}$, 且 $R_{\mathfrak{p}}$ 分式理想形如 ${\mathfrak{p}}^n{R}_{\mathfrak{p}}$ 即可.

$\square$

性质. 对 $K$ 中每一个非零 $R$ 分式理想 $I$, 仅有有限多个素理想 ${\mathfrak{p}}_i\subset R$, 其中 $1\le i\le n$, 使得 $v_{{\mathfrak{p}}_i}(I)\ne 0$.

证明. 首先证明 $I$ 为 $R$ 中理想的情形, 设素理想 ${\mathfrak{p}}_i(i\in {\mathbb{N}}_{+})$ 都使得 $v_{{\mathfrak{p}}_i}(I)>0$.

若 $I\subset {\mathfrak{p}}^{v_{\mathfrak{p}}(I)}$, 则 $I{\mathfrak{p}}^{-v_{\mathfrak{p}}(I)}\subset R$. 对素理想 ${\mathfrak{p}}^{\prime }\ne \mathfrak{p}$, 有 $v_{{\mathfrak{p}}^{\prime }}(I{\mathfrak{p}}^{-v_{\mathfrak{p}}(I)})=v_{{\mathfrak{p}}^{\prime }}(I)$. 因而$$I\subset I{\mathfrak{p}}_1^{-v_{{\mathfrak{p}}_1}(I)}\subset I{\mathfrak{p}}_1^{-v_{{\mathfrak{p}}_1}(I)}{\mathfrak{p}}_2^{-v_{{\mathfrak{p}}_2}(I)}\subset \cdots \subset R$$是理想的严格增链, 与 Noether 性质矛盾.

对一般的分式理想 $I$, 存在 $a\in R$ 使得 $aI=(a)I$ 是 $R$ 中的理想, 使得 $v_{\mathfrak{p}}(a)\ne 0$ 或 $v_{\mathfrak{p}}(aI)\ne 0$ 的素理想 $\mathfrak{p}$ 只有有限个. 对其余的素理想 ${\mathfrak{p}}^{\prime }$, 有$$v_{{\mathfrak{p}}^{\prime }}(I)=v_{{\mathfrak{p}}^{\prime }}(aI)-v_{{\mathfrak{p}}^{\prime }}(a)=0.$$于是命题得证.

$\square$

性质. 每一个非零分式理想 $I$ 可以唯一地写成 $I={\mathfrak{p}}_1^{n_1}\cdots {\mathfrak{p}}_t^{n_t}$ 的形式, 其中 ${\mathfrak{p}}_1,\dots ,{\mathfrak{p}}_t$ 是不同的素理想, $0\ne n_i\in \mathbb{Z}(1\le i\le t)$, 且 $n_i=v_{{\mathfrak{p}}_i}(I)$.

证明. 我们依然先对 $R$ 中的理想进行证明: 设 ${\mathfrak{p}}_1,\dots ,{\mathfrak{p}}_t$ 是全体使得 $v_{{\mathfrak{p}}_i}(I)>0$ 的素理想. 那么 $I^{\prime }=I{\mathfrak{p}}_1^{-v_{{\mathfrak{p}}_1}(I)}\cdots {\mathfrak{p}}_t^{-v_{{\mathfrak{p}}_t}(I)}$ 是 $R$ 中理想, 且 $v_{\mathfrak{p}}(I^{\prime })=0$ 对任意的素理想 $\mathfrak{p}$, 从而 $I^{\prime }$ 不含在任何素理想中. 故 $I^{\prime }=R$, $I={\mathfrak{p}}_1^{v_{{\mathfrak{p}}_1}(I)}\cdots {\mathfrak{p}}_t^{v_{{\mathfrak{p}}_t}(I)}$.

对一般的分式理想 $I$, 和之前一样, 我们将其写成 $(a{)}^{-1}{I}^{\prime }$ 的形式, 其中 $a\in R-\{0\}$, $I^{\prime }\subset R$ 是理想. 同样可以得到$$I={\mathfrak{p}}_1^{v_{{\mathfrak{p}}_1}(I)}\cdots {\mathfrak{p}}_t^{v_{{\mathfrak{p}}_t}(I)}.$$

$\square$

注记. 事实上, Dedekind 整环可以完全被这个性质刻画. 即若整环 $R$ 中每个非零理想存在唯一的素理想分解式, 则 $R$ 为 Dedekind 整环.

我们总结一下我们得到的结果:

性质. 若以 $\mathcal{J}(R)$ 表示 $R$ 的全体非零分式理想构成的集合, 则 $\mathcal{J}(R)$ 在乘法下构成群, 且这个群同构于非零素理想生成的自由 Abel 群: $$\mathcal{J}(R)\to \underset{\mathfrak{p}}{⨁}\mathbb{Z}\mathfrak{p},I\mapsto \sum _{\mathfrak{p}}{v}_{\mathfrak{p}}(I)\mathfrak{p}.$$同时 $I{R}_{\mathfrak{p}}={\mathfrak{p}}^{v_{\mathfrak{p}}(I)}{R}_{\mathfrak{p}}$.

推论. 有同构 $\mathcal{J}(R)\to \underset{\mathfrak{p}}{⨁}\mathcal{J}(R_{\mathfrak{p}}),I\mapsto I{R}_{\mathfrak{p}}$.

我们还可以将 $(K,R_{\mathfrak{p}})$ 对赋值 $v_{\mathfrak{p}}$ 进行完备化, 得到 $(\overline{K},{\overline{R}}_{\mathfrak{p}})$ 以及一个延拓的赋值 ${\overline{v}}_{\mathfrak{p}}$. 此时仍有理想的一一对应: $$\mathcal{J}(R_{\mathfrak{p}})\to \mathcal{J}({\overline{R}}_{\mathfrak{p}}),{\mathfrak{p}}^n{R}_{\mathfrak{p}}\mapsto {\overline{\mathfrak{p}}}^n{\overline{R}}_{\mathfrak{p}}.$$因而有同构 $\mathcal{J}(R)\to \underset{\mathfrak{p}}{⨁}\mathcal{J}({\overline{R}}_{\mathfrak{p}})$.

在建立了 Dedekind 整环的性质之后, 我们来看几个例子.

例子. 设 $K$ 是 $\mathbb{Q}$ 的有限扩张. 记 ${\mathcal{O}}_K$ 为 $K$ 中的极大 order, 即 $K$ 中的代数整数构成的环. 我们之后会证明这是一个 Dedekind 整环.

对一般的 order 而言, 整闭条件未必满足. 但如果取其整闭包 (也就是极大 order) , 就将其变成了一个 Dedekind 整环.

例子. 我们考虑如下的环: $$R=\mathbb{C}[x,y]/(x^2+y^2-1)\cong \mathbb{C}[x][\sqrt{1-x^2}].$$

可以证明, $R$ 是一个 Dedekind 整环, 其非零素理想由形如$$(x-a)R+(y-b)R,a^2+b^2=1$$的理想给出. 容易发现, $R$ 上的非零素理想和曲线 $x^2+y^2=1$ 上的点一一对应.

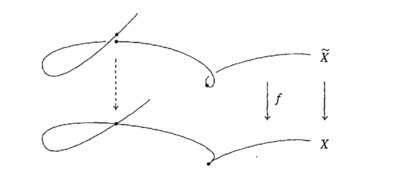
例子. 我们来看一个非 Dedekind 整环的例子. 考虑$$R=\mathbb{C}[x,y]/(y^2-x^2(x+1)).$$我们可以 “参数化” 这条曲线. 考虑 $\mathbb{C}[x,y]\to \mathbb{C}[t]$, 使得 $x\mapsto t^2-1,y\mapsto t^3-t$, 这诱导一个 $R\to \mathbb{C}[t]$ 的单射. 但这不是满射, 因为 $t$ 不在像中.

另一方面, 我们可以证明 $\mathbb{C}(t)$ 可以通过上面的嵌入实现为 $R$ 的分式域. 由于 $t$ 是 $R$ 上整元素, 且 $\mathbb{C}[t]$ 在 $\mathbb{C}(t)$ 中整闭, 我们得到 $R$ 的整闭包恰好是 $\mathbb{C}[t]$. 这说明 $R$ 不整闭, 故不是 Dedekind 整环, 但其整闭包 $\mathbb{C}[t]$ 是一个 Dedekind 整环.