基本概念 一个 (抽象) 李代数是指一个线性空间 V [ − , − ] : V × V → V
( 1 ) [ x , y ] = − [ y , x ]
( 2 ) [ x , [ y , z ]] + [ y , [ z , x ]] + [ z , [ x , y ]] = 0
一个李群是指一个配上光滑流形/复解析流形结构的群, 要求群运算、取逆元均与流形结构相容 (光滑/解析) . 李群间的态射是光滑的群同态.
李群 G T 1 G Lie ( G )
上面的定义不能看出为什么称单位元的切空间为李代数. 接下来, 我们要在切空间
T 1 G 上造出我们需要的李代数结构.
对任意实线性空间 V GL ( V ) gl ( V ) [ A , B ] = A B − B A gl ( V )
事实上, 任给一个向量 v ∈ T 1 G 1 G γ v ( t ) : R → G C → G
我们定义 exp : g → G , v ↦ γ v ( 1 ) gl ( V )
对一切 s , t ∈ R s , t ∈ C v ∈ T 1 ( G )
exp ( t v ) = γ v ( t )
exp (( s + t ) v ) = exp ( s v ) exp ( t v )
exp G 1 g 0
exp φ : G 1 → G 2 φ ∗ : Lie ( G 1 ) → Lie ( G 2 ) exp ( φ ∗ v ) = φ exp ( v )
既然
exp 在足够小的邻域上是可逆的, 对充分小的
x , y , 我们可设
exp ( x ) exp ( y ) = exp ( μ ( x , y )) , 其中
μ : g × g → g . 将其展开, 可以得到
μ ( x , y ) = x + y + λ ( x , y ) + ( deg ≥ 3 terms ) . 我们取 [ x , y ] = 2 λ ( x , y ) gl ( V ) [ − , − ]
此外, 注意到李群上有共轭作用给出的自同构: G → G , x ↦ gx g − 1 . g Ad g exp Ad g exp
我们同样记 Ad : G → GL ( g ) ad : g → gl ( g )
( 1 ) ad ( x ) ( y ) = [ x , y ]
( 2 ) ad [ x , y ] = ad x ad y − ad y ad x
这就给出了我们想要的李代数结构.
设 h g [ h , h ] ⊂ h g
若 [ g , h ] ⊂ h g h
设 H ⊂ G h ⊂ g H ⊲ G h ⊂ g G / H g / h
作为对李群的类比, 对一个流形
M , 我们可以考虑其全体光滑自同胚
Diff ( M ) . 一般来说, 这不是李群. 考虑单参微分自同胚
φ t : M → M , 对每个
m ∈ M ,
d t d φ t 在
t = 0 给出一个向量场. 因此, 对很靠近恒等的自同胚, 我们可以将其视为
M 上向量场. 因此
M 上的全体向量场
Vect ( M ) 可视为对 “李代数” 这一概念的模拟.
设 ξ Φ ξ t : M → M [ ξ , η ] Ψ ξ t Ψ η s Ψ ξ − 1 t Ψ η − 1 s = Ψ [ ξ , η ] t s + ( deg ≥ 3 terms ) .
[ − , − ] ∂ [ η , ξ ] f = ∂ η ( ∂ ξ f ) − ∂ ξ ( ∂ η f ) .
[ ξ , η ] = d t d ( Ψ ξ t ) ∗ η ( γ ( − t )) x i [ f i ∂ x i ∂ , g i ∂ x i ∂ ] = ( f i ∂ x i ∂ g j − g i ∂ x i ∂ f j ) ∂ x j ∂ .
定义李群 G M ρ : G → Diff ( M ) ρ ∗ : g → Vect ( M )
作用 ρ : G → M m ∈ M G m = { g ∣ g m = m , ∀ g ∈ G } . G h = { x ∈ g ∣ ρ ∗ ( x ) ( m ) = 0 } .
G / G m → M , g ↦ g m O m T m ( O m ) = g / h
设
A 是一个域
k ( = R 或 C ) 上的有限维结合代数, 那么
Aut ( A ) 是一个李群. 我们定义
Der ( A ) = Lie ( Aut ( A )) . 对李群 G Z ( G ) g { x ∈ g ∣ [ x , y ] = 0 , ∀ y ∈ g } .
接下来我们介绍 Campbell-Hausdorff 定理. 这个定理告诉我们, 李群的 “非交换” 结构的信息由其李代数完全确定.
对上面定义的 μ ( x , y ) μ ( x , y ) = x + y + 2 1 [ x , y ] + 12 1 ([ x , [ x , y ]] + [ y , [ y , x ]]) + ⋯ .
这说明李群和李代数在一定程度上 “相互对应”. 由此我们可以相信下面的定理:
( 1 ) G g
G ⊃ H ↦ Lie ( H ) G g
( 2 ) G 1 , G 2 G 1 G 1 → G 2
( 3 ) g G g g G / Z Z G
用抽象废话来说, 有限维李代数范畴和单连通李群范畴是等价的.
我们可以将一个实的李代数进行复化. 对一个实李代数 g g C = g ⊗ C . g g C
取 g = sl ( 2 , R ) g C = sl ( 2 , C )
取 g = u ( n ) g C = gl ( n , C )
设
G 是一个连通复李群,
g 是其李代数,
K ⊂ G 是一个实闭李子群. 若
Lie ( K ) 是
g 的实形式, 则称
K 为
G 的实形式.
接下来, 我们来重点关注 so ( 3 , R ) su ( 2 ) sl ( 2 , C )
对 so ( 3 , R ) J x = ⎝ ⎛ 0 0 0 0 0 1 0 − 1 0 ⎠ ⎞ , J y = ⎝ ⎛ 0 0 − 1 0 0 0 1 0 0 ⎠ ⎞ , J z = ⎝ ⎛ 0 1 0 − 1 0 0 0 0 0 ⎠ ⎞ [ J x , J y ] = J z , [ J z , J x ] = J y , [ J y , J z ] = J x .
su ( 2 ) 0 i σ 1 = ( 0 i i 0 ) , i σ 2 = ( 0 − 1 1 0 ) , i σ 3 = ( i 0 0 − i ) [ i σ 1 , i σ 2 ] = − 2 i σ 3 , [ i σ 3 , i σ 1 ] = − 2 i σ 2 , [ i σ 2 , i σ 3 ] = − 2 i σ 1 .
对 sl ( 2 , C ) e = ( 0 0 1 0 ) , f = ( 0 1 0 0 ) , h = ( 1 0 0 − 1 ) [ e , f ] = h , [ h , e ] = 2 e , [ h , f ] = − 2 f .
这几个李代数之间有着密切的关系. 首先, 我们知道 SU ( 2 ) SO ( 3 ) i σ 1 ↦ − 2 J x , i σ 2 ↦ − 2 J y , i σ 3 ↦ − 2 J z .
作为实流形有嵌入 SU ( 2 ) → SL ( 2 , C ) su ( 2 ) → sl ( 2 , C ) . sl ( 2 , C ) su ( 2 ) C → sl ( 2 , C ) . i σ 1 ↦ i ( e + f ) , i σ 2 ↦ e − f , i σ 3 ↦ i h .
在上面的各个李代数的例子里, 我们都可以定义一个双线性型:
x , y ↦ − Tr ( x y ) , 这个双线性型在
Ad G 的作用下保持不变.
一点表示论 这一部分主要介绍表示论当中的一些基本结果. 如无特殊声明, 我们总是考虑有限维的复表示.
设 G g V
一个李群 G V ρ : G → GL ( V )
一个李代数 g V ρ : g → gl ( V )
两个李群的表示之间的态射是指一个线性映射 V → V ′
一个李群表示 ρ : G → GL ( V ) ρ : g → gl ( V )
若 G G g
李群的具体结构一般比较复杂, 但其李代数是有限维的, 所以研究李代数的表示是比较方便的. 如果
G 不是单连通, 我们可以商去一个离散子群, 再取其万有覆叠.
我们知道, 一个 G C [ G ]
设 g g C g g C
子表示: 若 W ⊂ V G
按我们熟知的方式, 可以得到商表示.
直和与张量积: 两个空间 V 1 , V 2 G V 1 ⊕ V 2 , V 1 ⊗ V 2 G
李代数作用在张量积上的方式略有不同:
g → gl ( V 1 ⊗ V 2 ) , v ( x ⊗ y ) = ρ 1 ( v ) x ⊗ y + x ⊗ ρ 2 ( v ) y .
伴随表示: V V ∗ G ρ ∗ ( g ) ( v ∗ ) = ρ ( g − 1 ) t v ∗ .
表示 Hom ( V , W ) G = Hom G ( V , W )
若 V
如果 V
称 V V V = ⨁ V i n i
设 A : V → V A V λ
(Schur 引理) 若 V V → V
若 V , W V → W
设 V = ⨁ V i n i V i φ V → V φ ⊕ φ i
一个酉表示是指一个表示 V G
对李代数, 相应的条件是 ( ρ ( g ) v , w ) + ( v , ρ ( g ) w ) = 0
对酉表示来说, 我们可以取一个子表示的正交补, 从而任一可约表示是可分解的.
Haar 测度 我们总是希望通过巧妙地选取 Hermite 型, 把一个表示变成酉表示. 在有限群的时候, 只要取出一个 Hermite 型 ( − , − ) G ∣ G ∣ 1 g ∈ G ∑ ( gx , g y ) .
为了过渡到连续版本, 我们希望使用积分来代替求和: ∫ G ( gx , g y ) d g .
要实现积分, 首先要求可定向性. 好在对李群来说, 这是自动满足的: 在单位元处任意选取一个标架, 通过李群的平移作用, 我们自然能够将其延拓到整个李群上, 保持光滑性与非退化性. 从而李群总是可以定向的.
其次, 出于对积分收敛性的考虑, 我们希望操作紧支的函数. 但不幸的是, 通常我们还希望我们的对象有 G G C ( G ) → C , f → ∫ G f ω . f ≥ 0 μ ∫ G f ω = ∫ G f d μ . ω G μ G
紧李群上的 Haar 测度在相差一个常数因子的意义下是唯一的.
其证明使用了测度论中的 Lesbesgue-Radon-Nikodym 定理, 我们不在此给出.
我们总是可以适当地选择常数, 使得∫ X d μ = 1.
证明概要. 对
t ∈ g ,
μ t : A → μ ( A t ) 也是一个左不变的 Haar 测度. 于是
μ t 和
μ 相差一个常数
Δ ( t ) . 可以证明这是一个从
G 映到
R × 的连续函数. 但连续函数总把紧集映到紧集, 而
R × 的紧子群只有
1 .
有了 Haar 测度, 参考之前 “取平均” 的证明思路, 很容易证明有限维表示
V 都是半单的. 事实上, 对无限维表示同样如此: 考虑
V 的子表示族
{ V i } , 使得同一族中的表示空间两两交为
0 . 应用 Zorn 引理即可得到证明.
证明需要一点泛函分析的知识. 我们在此呈现黎景辉《拓扑群引论》中对紧群给出的更一般的证明:
证明. 设 ( π , V ) V π u ∈ V 1 ⟨ v , w ⟩ = ∫ G ( π ( x ) v , u ) ( u , π ( x ) v ) d x . ⟨ v , w ⟩ ≤ ∥ v ∥∥ w ∥ A ⟨ v , w ⟩ = ( A v , w ) ( A v , v ) = ∫ G ∣ ( π ( x ) v , u ) ∣ 2 d x ≥ 0 , x ↦ ( π ( x ) v , u ) ( A v , v ) = 0 ( π ( x ) v , u ) = 0 x v = 0 v = 0 A v = λ v λ > 0 ( A π ( x ) v , w ) = ∫ G ( π ( s ) π ( s ) v , u ) ( u , π ( s ) w ) d s = ∫ G ( π ( s ) v , u ) ( u , π ( s x − 1 ) w ) d s ) = ( A v , π ( x − 1 ) w ) = ( π ( x ) A v , w ) , π ( x ) A V λ = { v ∈ V ∣ A v = λ v } π ( x ) V λ ⊂ V λ
下面我们来证明 A A
设 v n v M ∥ v n ∥ ≤ M ∣ ( π ( x ) v n , u ) ( u , π ( s ) v n ) ( π ( s x − 1 ) u , u ) ∣ ≤ M 2 . n → + ∞ lim ∥ A v n ∥ 2 = n → ∞ lim ( A v n , A v n ) = n → + ∞ lim ∫ G ( π ( x ) v n , u ) ( u , π ( x ) A v n ) d x = n → + ∞ lim ∫ G ∫ G ( π ( x ) v n , u ) ( u , π ( s ) v n ) ( π ( s ) π ( x − 1 ) u , u ) d x d s = ∫ G ∫ G ( π ( x ) v , u ) ( u , π ( s ) v ) ( π ( s ) π ( x − 1 ) u , u ) d x d s = ∥ A v ∥ 2 . n → + ∞ lim ( A v , A ( v − v n )) = 0 n → + ∞ lim ∥ A v − A v n ∥ = 0 A
于是根据紧算子的谱分解定理,
V=\bigoplus_\limits{\lambda}V_\lambda . 同时
dim ( V λ ) < + ∞ . 每个
V λ 都是不变的.
由证明过程可以看出, 若 π π
Peter-Weyl 定理 我们知道, L 2
设 V , W G ρ ij V ( g ) ρ V ( g ) ij ∫ G ρ ij V ( g ) ρ k l W ( g ) = 0. f : V → V ∫ G ρ ij V ( g ) ρ k l V ( g ) = dim V δ ik δ j l .
对有限维表示
V , 我们选取一个 Hermite 内积
( − , − ) 使得
V 成为一个酉表示, 那么对偶空间
V ∗ 上也就有了相应的 Hermite 内积, 使其同样成为一个酉表示. 我们同样可以在空间
C ∞ ( G ) 上定义一个内积:
( f 1 , f 2 ) = ∫ G f 1 ( g ) f 2 ( g ) d g . 于是上面的
ρ ij V g 成为
C ∞ ( G ) 中两两正交的向量.
我们定义 m : V i ∈ Irr ( G ) ⨁ V i ∗ ⊗ V i → C ∞ ( G ) f ⊗ v ↦ ( g ↦ f ( gv )) .
其中
V i 上和
V i ∗ 上的内积诱导
V ∗ ⊗ V 上的内积:
( f 1 ⊗ v 1 , f 2 ⊗ v 2 ) = dim V ( f 1 , f 2 ) ( v 1 , v 2 ) , 进而诱导
V i ∈ Irr ( G ) ⨁ V i ∗ ⊗ V i 上的内积. 不难发现
m : V ⊗ V ∗ → C ∞ ( G ) 保内积, 因此是一个单射. 两边进行完备化, 我们得到
⨁ ( V i ∗ ⊗ V i ) → L 2 ( G ) . 由于映射保持内积, 这还是一个单射.
证明.
我们使用如下的 Weierstrass-Stone 定理: 任意可区分点的、含 1
我们想要证明: ⨁ V i ∗ ⊗ V i C ( G ) L 2 ( G ) L 2 ( G ) G
我们不妨把其中一个点取成单位元. 对任意
g = 1 , 取一个
1 的开邻域
U , 使得
U ∩ gU = ∅ . 于是
g 在
1 U 上的作用非平凡, 从而在
L 2 ( g ) 的某个不可约子表示
V i 上作用非平凡. 于是直和项
V i ∗ ⊗ V i 即可区分
g 和
1 . 剩余条件是容易验证的. 于是上述映射的像可以逼近连续函数, 从而取闭包后是整个
L 2 ( G ) .
矩阵的系数给出 V i ∗ ⊗ V i
所有不可约表示在某组基下的矩阵系数 ρ ij V ( g ) L 2 ( G )
现在我们来用表示论的观点看待 Fourier 级数.
考虑环面 T n R n 1 ( e i θ 1 , … , e i θ n ) . T n ( θ 1 , … , θ n ) ↦ ( m 1 θ 1 , … , m n θ n ) , m 1 , … , m n ∈ Z ( e i θ 1 , … , e i θ n ) ↦ ( e i m 1 θ 1 , … , e i m n θ n ) , m 1 , … , m n ∈ Z . L 2 ( T n )
除了矩阵系数之外, 我们还经常考虑不可约表示的特征标. 模仿有限群的情形, 可以得到其定义: χ V ( g ) = Tr ( ρ ( g )) = i ∑ ρ ii V ( g ) . L 2 ( G )
{ χ V ∣ V ∈ Irr ( G )} ( L 2 ( G ) ) Ad ( L 2 ( G ) ) Ad L 2 ( G ) G
sl ( 2 , C ) 如果没有特别声明, 我们总是研究有限维的不可约表示.
我们知道, sl ( 2 , C ) su ( 2 )
和之前一样, 我们取基e = ( 0 0 1 0 ) , f = ( 0 1 0 0 ) , h = ( 1 0 0 − 1 ) [ e , f ] = h , [ e , h ] = − 2 e , [ f , h ] = 2 f . e , f h V h
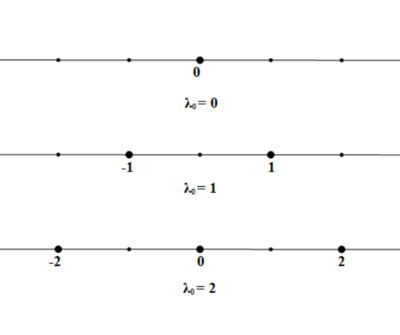
V = λ ⨁ V λ λ h
证明. 我们只要证明上式右侧是 g
对 v ∈ V λ h f v = f h v − 2 f v = ( λ − 2 ) f v f v ∈ V ( λ − 2 ) .
类似地, e v ∈ V ( λ + 2 ) λ ⨁ V λ g
我们看到一个有趣的现象: 在这个分解里,
e 和
f 的作用分别使这个分解中的
λ ——我们暂且称为权——增加
2 和减少
2 . 由于
V 是有限维的, 我们取使得
V λ = 0 的
λ 中实部最大者
λ 0 (
V λ 0 中的元素称为 “最高权向量”) . 此时
e 的作用已不能使权继续增大, 故
e 在
V λ 0 上的作用是
0 .
取 v ∈ V λ 0 V = n ≥ 0 ⨁ C f n v .
证明概要. 和之前的思路完全一致, 我们只需要证明右端对 e , f , h
由于 v e v = 0 h v = λ 0 v n h f k v = ( λ 0 − 2 k ) f k v , e f k v = k ( λ 0 − k + 1 ) f k − 1 v ,
由于
V 是有限维的, 存在一个最大的
n , 使得
f n v = 0 , 于是
e f n + 1 v = n ( λ 0 − n ) f n v = 0 . 从而我们得到
λ 0 = n , 且
f n + 1 v = 0 . 于是
V = 0 ≤ k ≤ n ⨁ V λ 0 − 2 k , 且每个
V λ 0 − 2 k 由
f k v 张成.
反过来, 对每个自然数 n sl ( 2 , C ) n e , f , h sl ( 2 , C )
我们来考虑 SO ( 3 )
SU ( 2 ) → SO ( 3 ) ± I − I = exp ( i π 0 0 − i π ) = exp ( i πh ) i πh ∈ ker ρ SO ( 3 ) sl ( 2 , C ) λ 0
有了 sl ( 2 , C ) sl ( 3 , C )
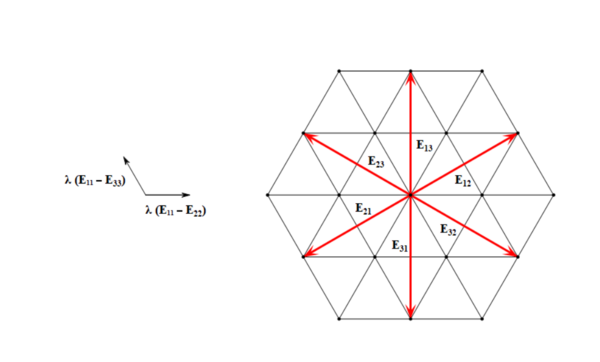
我们取基E ij ( i = j ) , E 11 − E 22 , E 11 − E 33 . h = span ( E 11 − E 22 , E 11 − E 33 ) h h
记 V λ = { v ∈ V ∣ ∀ A ∈ h , A v = λ ( A ) v , λ ( A ) ∈ C } .
完全一致的论证给出V = λ ⨁ V λ . λ ( A ) λ ( E 11 − E 22 ) λ ( E 11 − E 33 )
先前有关于 sl ( 2 , C ) sl ( 2 , C ) sl ( 3 , C ) E 11 − E 22 , E 12 , E 21 sl ( 2 , C ) sl ( 2 , C ) sl ( 3 , C ) E 12 E 21
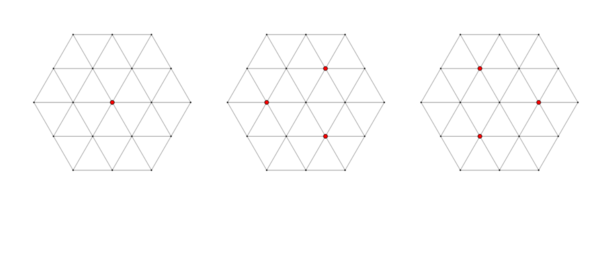
对剩余两个方向, 也同样如此. 于是表示的权应该在三个方向都具有对称性. 我们在图中展示几个不可约表示:
泛包络代数与 PBW 定理 接下来我们使用一些比较代数的手段来研究李代数本身的结构. 如果你愿意, 甚至可以暂时把李群的概念忘掉. 如无特殊声明, 我们讨论的都是域 k
在李代数上, 我们最感兴趣的是满足反对称性和 Jacobi 恒等式的李括号 [ − , − ] [ x , y ] = x y − y x .
为此, 我们要制造出这样一个乘法来. 对任意线性空间 V V T V = n ≥ 0 ⨁ T n V , T 0 V = k , T n V = V ⊗ n . k ( v 1 ⊗ ⋯ ⊗ v m ) ⋅ ( w 1 ⊗ ⋯ ⊗ w n ) = v 1 ⊗ ⋯ ⊗ v m ⊗ w 1 ⊗ ⋯ ⊗ w n v 1 ⊗ ⋯ ⊗ v m , w 1 ⊗ ⋯ ⊗ w n v 1 ⊗ ⋯ ⊗ v m ⊗ w 1 ⊗ ⋯ ⊗ w n T m V , T n V T m + n V
上面构造的张量代数 T V k k k A k V → A k T V → A
对李代数 g U g U g = T g / ( x y − y x − [ x , y ]) , x , y ∈ g .
从
T V 的泛性质就可以看出, 这是我们最 “经济” 的构造乘法的方式. 具体来说, 有如下性质:
设 A k ρ : g → A k ρ ( x ) ρ ( y ) − ρ ( y ) ρ ( x ) = ρ ([ x , y ]) U g → A
回忆一个李代数表示是指一个李代数同态
g → gl ( V ) = End k ( V ) , 我们可以将其提升为一个代数
U g 的表示. 换言之, 一个李代数
g 的表示相当于一个
U g 模. 于是我们可以用研究结合代数表示的方法来研究李代数的表示.
如果李代数 g [ x , y ] = 0 U g = S g g
需要注意的是, 尽管我们之前经常以矩阵表示李代数中的元素, 但是泛包络代数的乘法和矩阵的乘法未必是一样的. 比如在
sl ( 2 , C ) 里,
e , f , g 如我们之前所选取. 如果考虑矩阵乘法, 那么
e 2 = 0 . 但是在泛包络代数
U g 中,
e 2 = 0 . 这是因为矩阵的乘法是 “外来” 的东西, 而非李代数本身所反映的结构. 正如我们在上一讲中看到的那样, 在大部分
sl ( 2 , C ) 的表示里,
e 2 = 0 .
现在我们来关注 U g U g T g x y , y x x y − y x = [ x , y ] U g m k U m g k = U 0 g ⊂ U 1 g ⊂ ⋯ , U g = n ≥ 0 ⋃ U n g . U g
有如下性质:
( 1 ) x ∈ U p g , y ∈ U q g x y ∈ U p + q g
( 2 ) x ∈ U p g , y ∈ U q g [ x , y ] ∈ U p + q − 1 g
( 3 ) g x 1 , … , x n U m g x 1 p 1 ⋯ x n p n , p 1 + ⋯ p n ≤ m U g x 1 , … , x n
这些性质都不难用归纳的方式证出来, 我们将其留给有兴趣的读者.
( 1 ) U m g
( 2 ) U g Gr U g n ≥ 0 ⨁ U n g / U n − 1 g , U − 1 g = 0
我们还想寻求
U g 的一组基. 最自然的想法是诉诸上述性质
( 3 ) 中给出的元素
x 1 p 1 ⋯ x n p n . 幸运的是, 这确实是一组基. 这就是下面我们叙述的 Poincaré-Birkhoff-Witt 定理 (以下简称 PBW 定理) :
设 x 1 , … , x n g x 1 p 1 ⋯ x n p n U g
换言之, 有自然的同构 S g → Gr U g
证明概要. 为了证明线性无关性, 我们需要一个合适的表示, 使得这些元素的作用是线性无关的. 注意到定理断言
Gr U g ≅ S g , 我们可以考虑建立一个
U g 在
S g 上的表示. 我们要求
ρ ( x i ) ( x j 1 ⋯ x j n ) = x i x j 1 ⋯ x j n 如果
i ≤ j 1 ≤ ⋯ j n . 但我们还需要对
i > j 1 的情形确定
ρ ( x i ) 在
x j 1 ⋯ x j n 上的作用. 借助如下关系
ρ ( x i ) x j 1 ⋯ x j n = ρ ( x i ) ρ ( x j 1 ) x j 2 ⋯ x j n = ρ ( x j 1 ) ρ ( x i ) x j 2 ⋯ x j n + ρ ([ x i , x j 1 ]) x j 2 ⋯ x j n , 我们可以降低表达式的 “次数”. 通过归纳地构造映射
U g ⊗ ( 0 ≤ i ≤ n ⨁ S i g ) → S g , 我们得到一个良好定义的映射
U g → End ( S g ) . 最后只要验证这是一个李代数表示.
由 PBW 定理, 我们可以得到一些有用的推论:
( 1 ) g → U g
( 2 ) g 1 , g 2 g g = g 1 ⊕ g 2 U g = U g 1 ⊗ U g 2
( 3 ) U g
( 4 ) Char k = 0 g S g → U g , x 1 ⋯ x p ↦ p ! 1 σ ∈ S p ∑ x σ ( 1 ) ⋯ x σ ( p ) .
证明概要. ( 1 ) ( 3 ) ( 4 )
容易验证这是一个
g 表示的同态, 并且是单的. 由于复合
S g → U g → Gr U g 正是 PBW 定理给出的同构, 因而
S g 映满
U n g / U n − 1 g , 从而映满
U n g , 因此映满
U g .
幂零性与可解性 我们先前已经定义过子代数的概念. 出于对结合代数的模仿, 我们还希望定义商代数. 为此, 我们还要定义一个类似于结合代数中 “理想” 的概念. 这就是我们之前所定义过的:
定义一个李代数的理想是指一个子空间 h ⊂ g x ∈ h , y ∈ g [ x , y ] ∈ h
对子代数 h ⊂ g N g ( h ) = { x ∈ g ∣ [ x , h ] ⊂ h } h g h N g ( h )
由于李括号总是反交换的, 我们不需要强调左理想、右理想或是双边理想.
对理想 h ⊂ g g g / h g / h
对李代数同态 f : g 1 → g 2 ker f g 1 im f g 2 g 1 / ker f → im f .
设 I 1 , I 2 g I 1 + I 2 = { x + y ∣ x ∈ I 1 , y ∈ I 2 } , [ I 1 , I 2 ] = span k {[ x , y ] ∣ x ∈ I 1 , y ∈ I 2 } , I 1 ∩ I 2 g
我们称 [ g , g ] g z ( g ) = { x ∈ g ∣ [ x , y ] = 0 , ∀ y ∈ g } g
g / [ g , g ] h g / h [ g , g ] ⊂ h
我们可以考虑一下 gl ( n , k ) sl ( n , k ) i = j [ E ii − E jj , E ij ] = 2 E ij , E ii − E jj = [ E ij , E ji ] , gl ( n , k ) 0 gl ( n , k ) sl ( n , k ) sl ( n , k )
仿照群论的情形, 我们可以通过导出列和定义可解李代数和幂零李代数.
我们定义 g D i g D 0 g = g , D i + 1 g = [ D i g , D i g ] . D 0 g ⊃ D 1 g ⊃ ⋯ g D i g / D i + 1 g
如下条件等价:
( 1 ) n D n g = 0
( 2 ) g = a 0 ⊃ a 1 ⊃ ⋯ a k = 0 , a i + 1 a i a i / a i + 1
( 3 ) n [ ⋯ [[[ x 1 , x 2 ] , [ x 3 , x 4 ]] , [[ x 5 , x 6 ] , [ x 7 , x 8 ]]] ⋯ ] = 0 x 1 , ⋯ , x 2 n
称满足上述三条性质的李代数为可解的.
我们知道可解群与方程的根式解是关联的. 实际上, 可解李代数与一个微分方程是否能用 “积分” 的方法求解有关.
我们定义 g D i g D 0 g = g , D i + 1 g = [ D i g , g ] . D 0 g ⊃ D 1 g ⊃ ⋯ g D i g / D i + 1 g g / D i + 1 g
如下条件等价:
( 1 ) n D n g = 0
( 2 ) g = a 0 ⊃ a 1 ⊃ ⋯ a k = 0 , [ g , a i ] ⊂ a i + 1
( 3 ) n [ ⋯ [[[ x 1 , x 2 ] , x 3 ] , x 4 ] ⋯ ] = 0 x 1 , ⋯ , x n [ g , − ]
称满足上述三条性质的李代数为幂零的.
( 1 ) g g C
( 2 ) g g
( 3 ) g g
( 4 ) I ⊂ g I g / I g
证明. ( 1 ) ( 2 )
( 3 ) D i g ⊂ D i g
( 4 ) φ : g → g / I φ ( D i g ) = D i ( g / I ) n φ ( D n g ) = 0 ⇒ D n g ⊂ I k D k I = 0 D n + k g ⊂ D k I = 0.
(请考虑: 如果把可解换成幂零, 这个证明成立吗? )
我们考虑线性空间 V F 0 = V 0 ⊂ V 1 ⊂ V 2 ⊂ ⋯ ⊂ V n = V , dim ( V i + 1 ) = dim ( V i ) + 1 b ( F ) = { x ∈ gl ( V ) ∣ x V i ⊂ V i , 0 ≤ i ≤ n } n ( F ) = { x ∈ gl ( V ) ∣ x V i ⊂ V i − 1 , 0 ≤ i ≤ n } b n a k ( F ) = { x ∈ gl ( V ) ∣ x V i ⊂ V i − k , k ≤ i ≤ n } b ( F ) = a 0 n ( F ) = a 1 x ∈ a k y ∈ a l x y ∈ a k + l D i n ⊂ a i + 1 n
至于 b V i + 1 / V i x , y ∈ b x y y x V i + 1 / V i [ b , b ] ⊂ a 1 D i + 1 b ⊂ a 2 i b
我们可以把 b n b n ⊂ b
注意到, b x = diag ( λ 1 , … , λ n ) [ x , E ij ] = ( λ i − λ j ) E ij
Lie 定理和 Engel 定理 在这一节, 我们假定 k 0
在线性代数里我们见过这样的事实: 一族相互交换的矩阵可以被同时上三角化.“相互交换” 的条件意味着这些矩阵实际上构成了一个李括号平凡的李代数. 这族矩阵可被同时上三角化的事实可以被推广, 这就是我们将要叙述的 Lie 定理:
设 ( V , ρ ) g ρ ( x ) ( x ∈ g )
和线性代数中的情形一致, 我们首先来证明如下引理:
在定理的假设下, 存在 v ∈ V − { 0 } ρ ( x ) ( x ∈ g )
证明. 我们对 dim ( g ) dim ( g ) = 0 , 1
如果 dim ( g ) > 1 dim ([ g , g ]) < dim ( g ) g ′ g g 1 g = g ′ ⊕ k x g ′ g v ∈ V g ′ w ∈ g ′ w v = λ ( w ) v
考虑由 x n v W g ′ w ∈ g ′ w x n v = x w x n − 1 v + [ w , x ] x n − 1 v = ⋯ = x n w v + k < n ∑ x k a kn v , a kn ∈ g ′
现设 n v , xv , … , x n v x n + 1 v x i v ( 1 ≤ i ≤ n ) W w ∈ g ′ ρ ( w ) λ ( w ) Tr W ( ρ ( w )) = ( n + 1 ) λ ( w ) w ∈ g ′ Tr W ([ x , w ]) = 0 λ ([ x , w ]) = 0 w xv = x w v + [ w , x ] v = x w v w x n v = x n w v = λ ( w ) x n v . W − { 0 } g ′ w x
由引理我们立即得到 Lie 定理的证明:
证明. 对
dim ( V ) 进行归纳.
dim ( V ) = 1 时无需任何证明, 设
dim ( V ) = n + 1 ≥ 2 , 取
v 为
g 中元素的一个公共特征向量, 在商空间
V / k v 中取一组基
v 1 ′ , … , v n ′ , 使得
g 中元素的矩阵是上三角的. 将
v i ′ 提升到
v i ∈ V , 则在基
v , v 1 , … , v n 下
g 中元素的矩阵都是上三角的.
( 1 ) g
( 2 ) g g 0 ⊂ I 1 ⊂ I 2 ⊂ ⋯ ⊂ I n = g I k + 1 / I k
( 3 ) g [ g , g ]
证明. ( 1 )
( 2 ) g
( 3 ) 由于
g / [ g , g ] 交换,
[ g , g ] 的可解性自动推出
g 的可解性. 反之, 根据 Lie 定理在伴随表示上的应用, 存在旗
F 使得
g ⊂ b ( F ) , 从而由上一节的例子得到
[ g , g ] ⊂ n ( F ) , 故
[ g , g ] 是幂零的.
对幂零李代数, 我们当然期望得到更强的结论, 但仅仅把 Lie 定理中的 “上三角” 换成 “严格上三角” 显然是不对的 (比如, 令交换李代数 g
若 g ⊂ gl ( V ) g
这个定理的证明和 Lie 定理的证明非常相似. 我们也需要一个引理:
在定理假设下, 存在 v ∈ V − { 0 } g
证明引理. 首先, 让我们注意到这样一个事实: 如果 x ad x x x L x R x L x , R x n ad x n = ( L x − R x ) n = 0. dim ( g ) dim ( g ) = 0 , 1
当 dim ( g ) ≥ 2 g ′ = g g g ′ g g ′ g ′ g / g ′ g ′ g / g ′ x ∈ g − g ′ [ g ′ , x ] ⊂ g ′ N g ( g ′ ) g ′ g g ′ g ′ 1 g / g ′ g g ′ g ′ 1 g = g ′ ⊕ k x
根据归纳假设, 存在
V 中的非零元素
w , 使得
w 被
g ′ 零化. 记所有这样的
w 生成的子空间为
W . 显然
W 是
g ′ 不变的. 由于对任意
w ∈ W 和
y ∈ g ′ , 有
[ y , x ] ∈ g ′ , 故
y x w = x y w + [ y , x ] w = 0. 从而
W 是
g 不变子空间. 我们取
w ∈ W 是
x 的一个特征向量, 则由
x 幂零知其特征值为
0 , 故
w 就是我们需要的向量.
由引理对 dim ( V )
作为推论, 我们可以得到 Engel 定理:
g x ∈ g ad x : y ↦ [ x , y ]
证明. “⇒ [ g , − ] ad x ( x ∈ g )
“
⇐ ” 对伴随表示, 由上面的定理, 我们可以将
g 嵌入某个
n ( F ) 中, 因而是幂零的.